多需求多类型自提点选址分配问题
2018-12-19李珍萍毛小寸
李珍萍,毛小寸
(北京物资学院 信息学院,北京 101149)
0 引言
自提服务可以解决投递时间不对称、快递员等待时间长、包裹丢失等问题,有效提高一次配送成功率,是解决快递配送“最后一公里”问题的有效途径。从顾客角度而言,顾客在网上购物时可以选择自提服务并根据配送地点选择便利的自提点位置;从快递企业角度而言,将选择自提服务的客户需求以相对大批量的方式集中配送至自提点,可以实现规模经济效应。目前已有的自提点类型包括便利店自提点、智能快件箱、小区物业自提点、校园自提点、Amazon Locker、DHL Packstation等,主要划分为有人值守和无人值守两类[1],不同类型自提点的处理能力(容量、服务种类)、建设成本、覆盖半径、对顾客的吸引力(服务时间、便利性)均不相同。因此,快递企业如何确定各种类型自提点的建设位置以及每个自提点的服务范围,是提高市场顾客占有率、解决最后一公里问题的关键。
国外对自提点相关问题的研究主要集中于自提模式、自提意愿、配送服务选择均衡问题等方面,Xu等[2]提出联合投资模式来运营“集中交付点”;Visser等[3]研究城市驾车购物、送货上门和就近取货点3种配送服务策略的行程次数和行驶里程,得出配合使用送货到家和就近取货点可减少城区内13%的道路占有率;Hübner等[4]在全渠道零售杂货店的最后一公里交付的战略规划框架中,对配送模式中的杂货店自提模式分店内(in-store),附加(attached)和孤立(solitary)3种具体的模式进行研究;Wang等[5]根据配送模式的操作流程建立不同类型的配送车辆路径规划模型和K-means聚类模型,研究电子商务物流最后一公里送货上门(Attended Home Delivery, AHD)模式、自助收发箱Reception Box, RB)模式和顾客自提站(Collection-And-Delivery Points, CDPs)模式决策问题;陈义友等[6]将顾客有限理性行为引入最后一公里配送服务的研究中,认为顾客根据自身期望的效用最大目标选择收货方式是基于顾客不完全理性行为的决策。
由于国内与国外在人口分布及生活方式等方面的巨大差异,国内学者主要借鉴国外学者在配送模式方面的研究成果研究符合中国特色的自提点选址问题。
周林等[7]综合考虑送货上门和顾客自提两种服务,建模并设计两阶段模拟退火算法求解多容量终端选址—多车型路径集成的优化问题;李梅[8]以运输成本、建站成本和距离惩罚成本最小化为目标建立自提点的选址模型;杨朋珏等[9]针对送货上门和自行取货配送模式构建满意度、效率的多目标城市末端网点选址模型,但未考虑自提点类型不同对顾客选择的影响;陈义友等[10]用多项 Logit模型(MultiNomial Logit model, MNL)模型刻画顾客的有限理性行为,用Erlang-B模型描述自提点拥堵情形构建自提点选址模型,并用多种算法求解;陈义友等[11]考虑自提点类型,用凹凸函数刻画消费者的满意度,通过设计拉格朗日松弛算法求解基于逐渐覆盖的自提点选址模型,但是未考虑不同类型自提点服务功能差异对选址结果的影响。已有研究成果表明,影响顾客选择自提服务的因素很多,其中包括自提点的类型、覆盖半径[12]、处理能力、服务能力、建设成本、自提点的吸引力、顾客满意度等,现有的关于自提点选址问题的研究中,大部分只考虑了一两个因素的影响,而且都是针对顾客只有一种需求的情况开展研究。
本文主要考虑顾客同时有自提和退换货两种需求下的自提柜、快递企业自建网点和与便民机构合作3种类型的自提点选址分配问题。在综合考虑不同类型自提点的建设成本、服务功能、服务能力、顾客满意度等因素的前提下,建立自提点选址—分配问题的数学模型并设计求解模型的算法,以降低企业总的运行成本。
1 问题描述及数学模型
网络消费者在地理空间上除了分布范围广之外,还呈现显著的空间集聚性,即在同一细粒度地理空间会存在多个客户,如学校、商场、小区等[13]。为研究多需求多类型自提点选址分配问题,本文将每个细粒度地理空间看作为一个客户群,每个客户群为一个需求点,每个需求点的顾客有一种或两种不同类型的需求(取货、退换货),围绕物流最后一公里配送需求特征展开以总建设成本极小化为目标的选址—分配方案研究。
多需求多类型自提点选址分配问题可以描述为:在给定的物流末端配送网络中有n个需求点,一个需求点存在一种或两种不同类型的需求(取货、退换货),已知各个需求点的位置和对两种不同类型服务的需求量;配送网络中有3种不同类型的备选自提点(自提柜、自建网点型、便利店型)共m个,每个备选点可以提供一种或两种服务;已知各个备选自提点的位置、建设成本、可提供的服务类型和最大服务能力等,在一定的顾客满意度水平下,企业如何确定各种类型自提点的建设数量、建设位置和每个自提点的服务范围,才能使总建设成本最小。
1.1 模型假设
(1)自提柜型自提点只能提供自提服务,快递企业自建网点型和与便民机构合作型两类自提点可以提供自提和退换货两种服务。
(2)每个需求点的同一种需求由一个自提点满足,不同服务需求可由多个类型的自提点满足。
(3)需求点对自提点的服务满意度是需求点到自提点的距离rij的非增函数,本文采用凹凸覆盖函数刻画的距离引力[10]计算顾客满意度,具体函数关系为
(1)
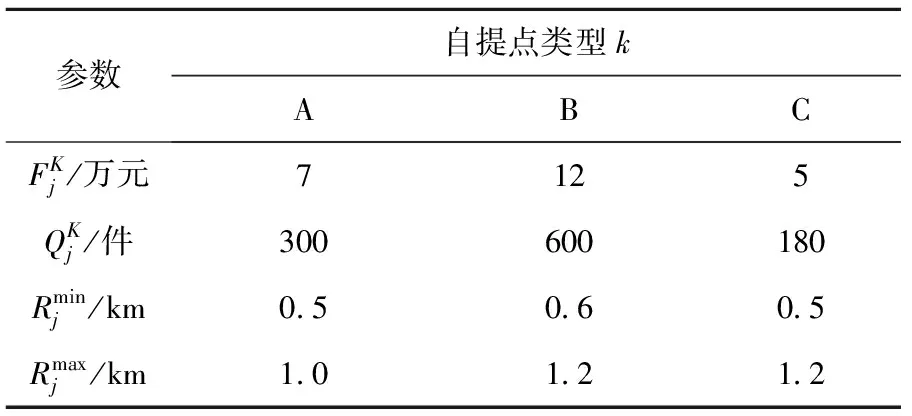
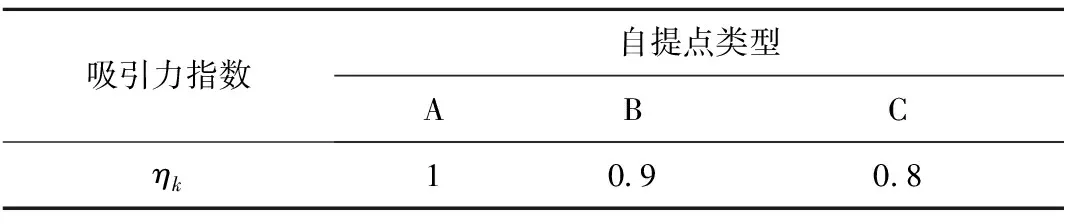
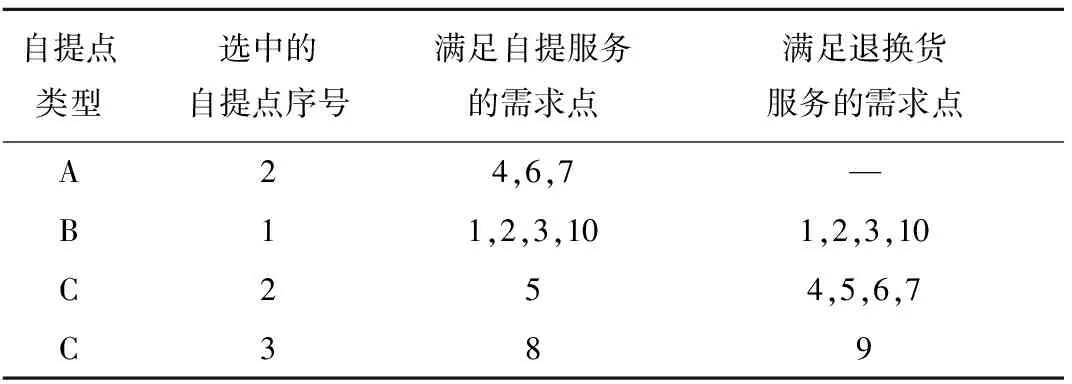
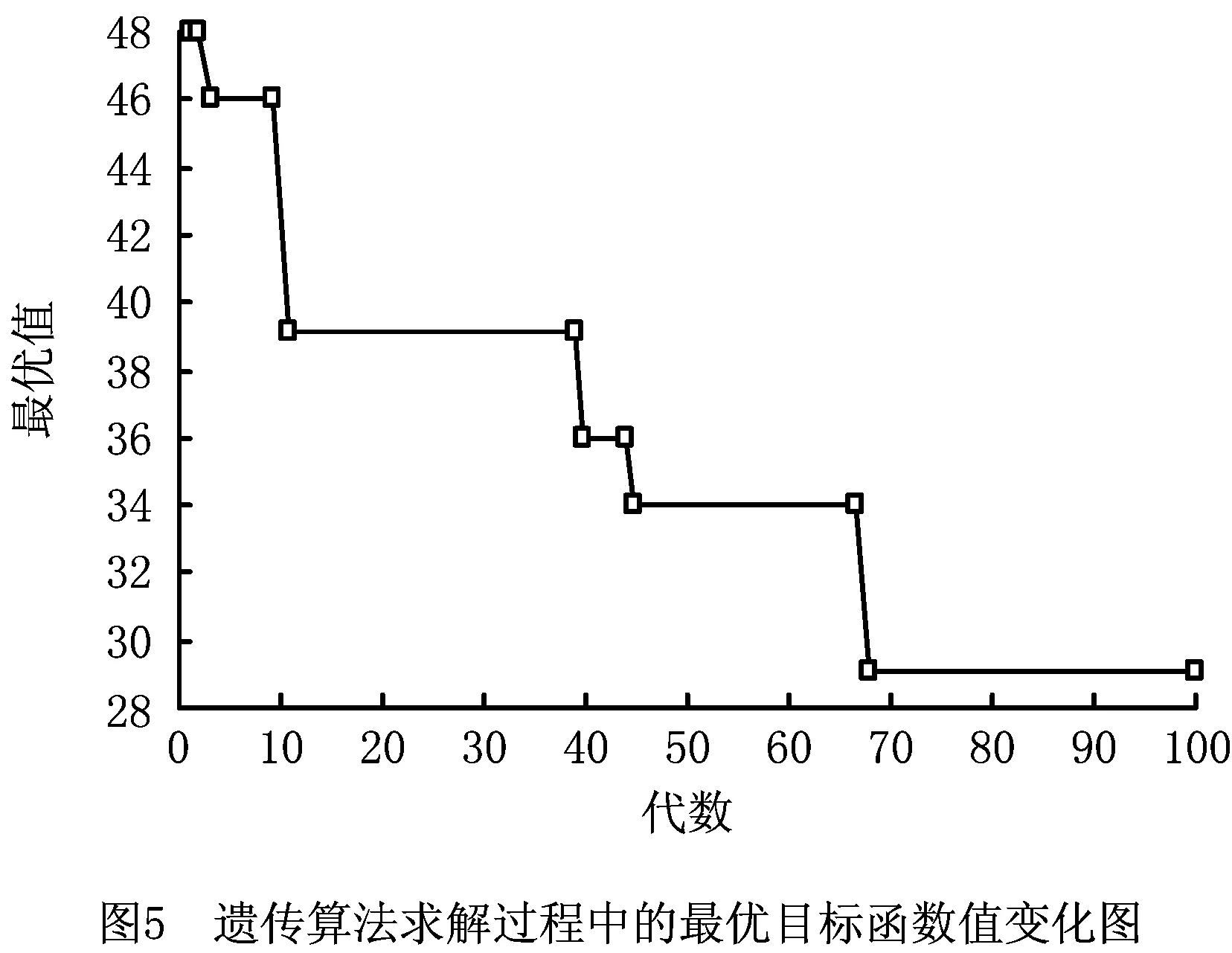
其中:r和R为已知参数,且r 为了建立多需求多类型自提点选址分配问题的数学模型,定义如下符号: I表示需求点的集合; J表示候选自提点的集合; K表示自提点类型的集合; L表示服务类型的集合,L={1,2}; B表示企业计划的投资金额; ηk表示k类型自提点对顾客的吸引力,ηk∈[0,1],k∈K; Rk表示第k种类型自提点的最大覆盖半径; rk表示第k种类型自提点的最小覆盖半径; αk表示对第k类候选自提点设置的最低顾客满意度值; i∈I,j∈J,k∈K。 (2) 定义如下决策变量: (3) (4) (5) (6) (7) (8) (9) (10) 其中:目标函数(3)表示极小化自提点的总建设成本;约束(4)表示各种类型自提点服务需求点的总需求量不超过各个自提点的最大处理能力;约束(5)表示每个需求点若有某一种服务需求,则这种需求恰好由一个自提点满足;约束(6)保证提供服务的自提点到需求点的顾客满意度大于预先设定值;约束(7)表示若某个备选点对应需要提供服务的需求点,则必须在该备选点建立自提点;约束(8)表示建立的自提点至少满足一个需求点的一种服务需求;约束(9)和(10)表示变量的取值约束。 虽然多需求多类型自提点选址分配问题可以表示为一个整数规划模型,但由于模型中的约束条件和变量较多,很难在短时间内通过直接求解整数规划模型得到最优解。本章根据整数规划模型的特点设计遗传算法(Genetic Algorithms, GA)求解多需求多类型自提点的选址分配问题,并通过MATLAB软件编程计算,验证模型和算法的有效性。 考虑3种类型自提点和两种类型服务需求(自提、退换货)。3种类型自提点中的自提柜型自提点只能提供自提服务,首先计算各个需求点到各类型候选自提点的顾客满意度矩阵,其中行表示需求点,列表示候选自提点,3种类型自提点的排列顺序依次为自提柜型、快递企业自建网点型和与便民机构合作型,根据多需求多类型自提点选址分配问题的特点设计染色体编码规则,并根据满意度矩阵进行染色体编码,生成初始种群。 遗传算法操作规则如下: (1)染色体编码 结合本文所建立的数学模型,定义染色体编码规则如下: 1)根据需求类型划分,每一条染色体由第Ⅰ类染色体片段即(自提类)和第Ⅱ类染色体片段(即退换货类)组成,如图1所示。图中:列表示有A,B,C 3种类型自提点,其数量分别为3,2,3;行表示有4个需求点,前4行表示4个需求点的自提需求,后4行表示4个需求点的退换货需求;第1行第1列的1表示第1个需求点的自提需求由A类型的第1个候选自提点服务,以此类推。解码得到多需求多类型自提点选址分配模型的一个可行解。 2)每一条染色体片段均是一个0-1矩阵,矩阵的每行对应一个需求点,每列对应一个自提点,如果需求点i的相应类型需求由自提点j提供服务,则矩阵中第i行第j列的元素等于1,否则等于0。 例如,图1中矩阵第1行第1列的元素1表示需求点1的自提需求由A类型中的1号自提柜提供服务;矩阵第5行第1列的元素0表示需求点1的退换货服务不是由A类型中的1号自提柜提供。 3)因为需求点的一种服务需求只能由一个自提点提供服务,所以染色体矩阵中每行有且只有一个元素(基因位)的值为1。 (2)初始种群的生成 采用将某些先验知识转化为必须满足的条件,并在满足约束条件的解中随机抽取个体构成初始种群的方法[14]。本文采用0-1矩阵编码方式,将需求点到对应服务类型自提点的顾客满意度值小于给定值αk的位置赋值为0,根据自提点服务能力约束和顾客满意度约束,按照轮盘赌法确定为需求点服务的自提点,将对应位置赋值为1,其余位置赋值为0。以此类推,按照预先设计的编码规则随机生成相应的染色体编码矩阵,直至生成足够多的个体构成GA的初始种群。 (3)适应度函数 根据将每个个体对应的染色体解码后的解可以求出每个个体对应的目标函数值,即各类型自提点建设总成本,第s个个体对应的目标函数值 (11) 由于模型中的目标函数为最小化问题,本文采用种群对应的最大目标函数值的两倍(即2max(objv))减去objv(s),作为对应个体的适应度值[15],即 FitV(s)=2max(objv)-objv(s)。 (12) (4)选择操作 本文采用轮盘赌法对个体进行选择操作。 (5)交叉操作 由于每个染色体由两类染色体片段组成,进行交叉操作时,选择同类片段染色体进行位点交换,一个个体对应的两个染色体片段的交叉位点相同。交叉规则设计如下:本文交叉采用双亲双子单点交叉,从种群中取出奇数位的个体和相邻的偶数位个体组成个体对,即父代P1和父代P2,按照给定的交叉概率选择一部分个体对进行交叉操作。对于需要进行交叉的个体对,随机选择交叉点位置pos,将父代P1中第Ⅰ类染色体片段的[pos:n]行与父代P2中第Ⅰ类染色体片段的[pos:n]行互换,同时将父代P1中第Ⅱ类染色体片段的[n+pos:2n]行与父代P2中第Ⅱ类染色体片段的[n+pos:2n]行互换产生两个子代个体S1,S2,如图2所示。 判断生成的两个子代个体对应的解是否都满足自提点处理能力约束和顾客满意度约束,若不满足则重新进行交叉操作,直至生成满足约束条件的子代个体。若对两个个体交叉若干次后(本文设置最大交叉次数n1=100次)仍未产生都满足约束条件的子代个体,则这两个个体不再进行交叉操作。交叉操作完成后计算个体的目标函数值,判断交叉操作后最优个体的目标函数值是否优于上代种群中最优个体的目标函数值,若是则不再进行变异操作直接进入下一代,否则进行变异操作。 GA交叉部分的计算步骤如下: 步骤2按照交叉概率随机选取若干对父代个体参与交叉操作。算法伪代码如下: 步骤3当累计交叉次数小于100时,whilen1<100,令n1=n1+1,随机选择交叉位置,对两个父代个体中的两类染色体分别进行交叉操作,产生两个临时子代个体,将两个临时子代个体解码形成两个解。 步骤4判断交叉后的两个临时子代个体对应的解是否满足容量约束。若不满足容量约束,则返回步骤3;若满足容量约束,则转步骤5。 步骤5判断满足容量约束的两个临时子代对应的解是否满足顾客最低满意度约束。若不满足顾客最低满意度约束,则返回步骤3;若满足顾客最低满意度约束,则保留交叉后的两个临时子代个体,令i=i+1,转步骤2。 步骤6如果n1=100,即个体交叉100次仍未产生满足约束条件的子代个体,则不再进行交叉操作,直接保留交叉前的两个父代个体,令i=i+1,转步骤2。 步骤7当n1=100时,结束while循环,返回步骤2。 步骤8结束for循环。 步骤9计算交叉后的种群中每个个体对应的目标函数值和适应度函数值,求出交叉后种群对应的最优目标函数值min(new_objv)。判断交叉后种群的最优目标函数值min(new_objv)是否小于种群进化过程中产生的最优个体对应的目标函数值min(objv),若min(new_objv) (6)变异操作 变异操作是改变染色体编码串上的部分基因值,从而提高种群的多样性。本文采用在两段染色体片段中分别交换行向量的变异方法,即在选定个体的染色体片段中随机产生两个交叉点,互换两个交叉点对应的行,得到新的子代个体。例如将上例的染色体A进行变异,如图3所示。 变异操作是在交叉操作生成的子代最优个体不如上一代最优个体的情况下进行的。预先设置变异概率参数pm,根据变异概率选择一部分个体进行变异操作。对于每一个参与变异操作的个体,判断变异后对应的解是否满足自提点处理能力约束和顾客满意度约束,若不满足则重新进行变异操作,直至生成满足约束条件的子代个体。若对某个个体变异若干次后(本文设置最大变异次数n2=100次)仍未产生满足约束条件的子代个体,则不再进行变异操作。变异操作完成后计算每个个体的目标函数值,判断变异操作后最优个体的目标函数值是否优于上代种群中最优个体的目标函数值,若是,则保留该种群进入下一代;否则,先用上代最优个体替换变异后的最坏个体,然后进入下一代。 (7)终止规则 当迭代次数达到设定的最大次数后,算法终止。 (8)遗传算法流程图 遗传算法的具体流程如图4所示。 根据某城区的居民分布情况将该城区划分为10个需求点,其中需求点8只有自提需求,需求点9只有退换货需求,其余8个需求点均有自提和退换货服务两种需求。已知每个需求点的自提需求量qi(件)和退换货服务需求量pi(件),该区域有3种类型候选自提点,其中只能提供自提服务的自提柜型候选点(A类)为nA(个),可以提供自提和退换货服务的企业自建网点型候选自提点(B类)为nB(个),可以提供自提和退换货服务的与便民机构合作型候选自提点(C类)为nC(个);根据对各个小区居民的问卷调查,设置最低顾客满意度值αk和不同备选自提点对顾客的吸引力ηk。不考虑快件的体积和重量,不同类型自提点服务参数(建设成本、服务能力,以及最小、最大覆盖半径)的设置如表1所示;不同备选自提点对顾客的吸引力ηk如表2所示;各个需求点的位置坐标已知,各个需求点对应的各类型需求量如表3所示。需求点到备选自提点的距离rij可以根据位置分布算出。 表1 不同类型自提点服务参数设置 表2 不同类型自提点对应的吸引力指数η值 表3 各个需求点对应的两种类型服务的需求量 件 本文设定初始种群大小为50,最大进化代数为100,交叉概率为0.8,变异概率为0.02,各类型自提点的最低顾客满意度值αk均为0.85,无效交叉次数最大值n1=100,无效变异次数最大值n2=100。利用MATLAB R2012a软件编程,在Intel(R)Core(TM)i5-480M@2.67 GHz CPU,4 GB内存电脑上运行5 s,得到的最优计算结果如表4所示。 表4 最低顾客满意度为0.85时的选址结果 在利用MATLAB运行GA求解的同时,本文也利用Lingo 11.0软件编写了直接求解整数规划模型的程序,结果发现Lingo程序求出来的全局最优解与GA得到的最优解相同(如表4),可见利用本文设计的GA求得的最优解即为全局最优解。最优目标函数值为29万元,最优解对应的自提柜类型(A类)、快递企业自建网点型(B类)、与便民机构合作型自提点(C类)的建设数量分别为1,1,2;表5所示为各类型自提点的最优选址—分配结果;图5所示为利用GA求解过程中最优目标函数值与迭代次数之间的变化关系;图6所示为GA求出的每个自提点与服务需求点之间的分配关系。与Lingo程序直接求解整数规划模型相比,利用GA可以在较短时间内得到问题的最优解,特别是随着问题规模的增大,采用GA求解的优势更加明显。 表5 遗传算法求出的最优选址—分配结果 本文模型以自提点的总建设成本极小化为目标,约束条件为顾客满意度不低于最低满意度值αk,而顾客满意度和自提点总建设成本之间存在密切联系,下面重点分析顾客的最低满意度αk与自提点总建设成本之间的关系。 由式(2)可以看出,顾客满意度是顾客到自提点距离的非增函数,提高顾客最低满意度值αk相当于减小了各个自提点的有效服务半径,由此需要建设更多自提点才能覆盖所有需求点,从而需要更多的建设成本。可见,模型中设定的最低满意度值αk越大,最优解对应的自提点总建设成本越大。 本例通过选取不同的顾客最低满意度值分别求解模型,得到最低顾客满意度值αk与自提点建设总成本之间的关系,如图7所示。可以看出,当企业将最低满意度设为91.2%时,各类型自提点的总建设成本最优值为29万元;当企业将最低顾客满意度设为100%时,各类型自提点的总建设成本最优值为39万元。实际中,快递企业可根据对顾客群体的调查,确定满意度最低值αk的设定方案,根据模型计算自提点总建设成本,再结合企业投资预算进一步确定有利于提高顾客最低满意度的自提点选址—分配方案。如在上述案例中,当设定顾客最低满意度为0.85时,用本文模型和算法得出的最优选址分配方案对应的总建设成本为29万元,根据最低顾客满意度和总建设成本的灵敏度分析图可知,在保持总建设成本为29万元的前提下,通过优化选址分配方案可以使顾客的最低满意度提高到91.2%。 与一般选址问题不同的是,多需求多类型自提点选址分配问题考虑顾客需求的多样性,以及不同类型自提点的服务功能、覆盖半径、容量大小、建设成本、对顾客的吸引力等多方面因素。本文考虑自提与退换货服务两种需求,并在一定顾客满意度约束下设计GA求解建设成本最小的多类型自提点选址—分配方案。算例分析结果显示,GA能在较短时间内求得问题的近似最优解,验证了模型和算法的有效性,通过多类型自提点的组合布局能更有效、更经济地满足顾客需求,为快递企业快速抢占末端市场、提高竞争力提供了理论依据。但由于不同类型自提点的处理能力在实际生活中具有较大差异,容量差异对自提点的建设成本也存在较大影响,未来可以在考虑同一类型自提点容量设置的情况下研究多类型自提点选址分配问题,以及同时考虑顾客满意度最大化与建设成本最小化的多目标多需求多类型自提点选址分配问题。1.2 符号和变量说明

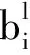
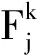
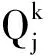

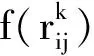
1.3 模型建立
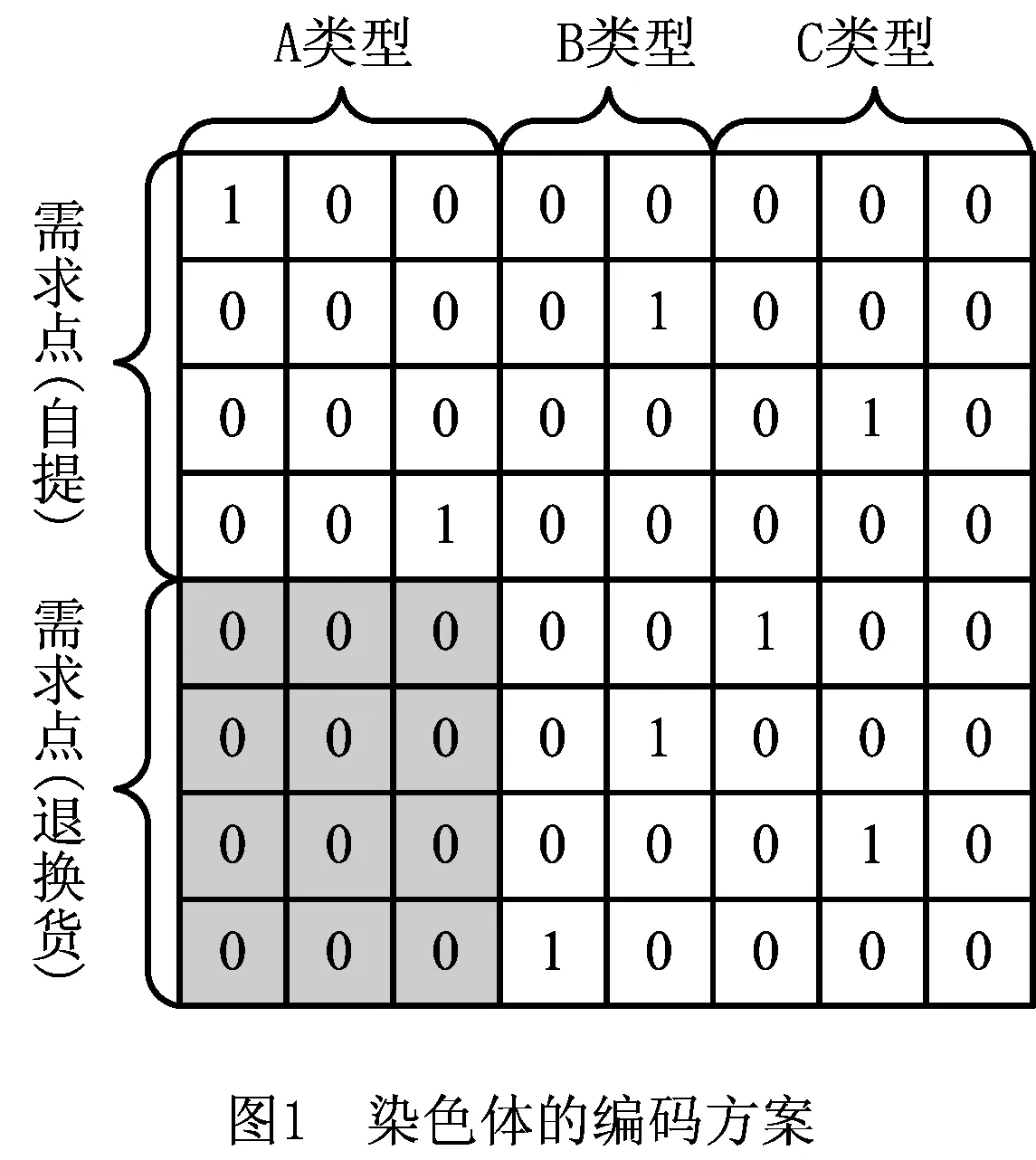
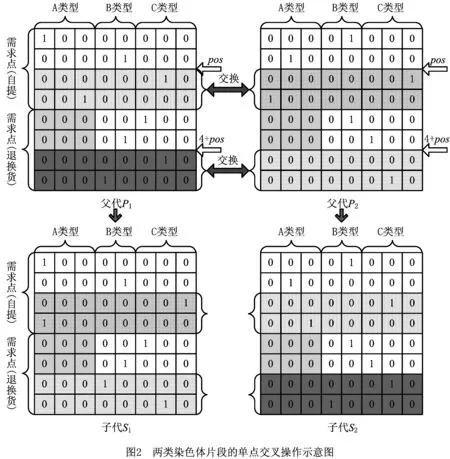
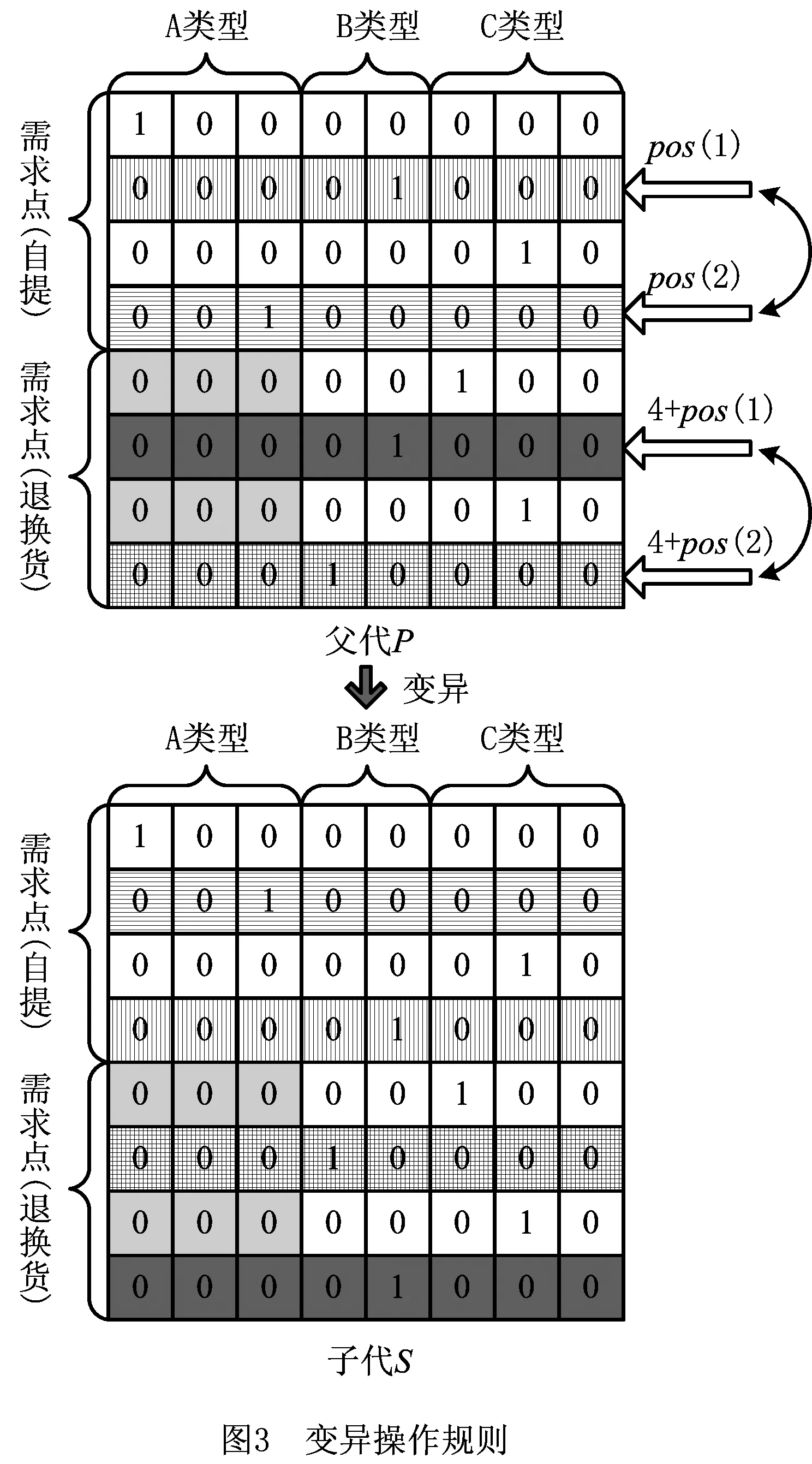
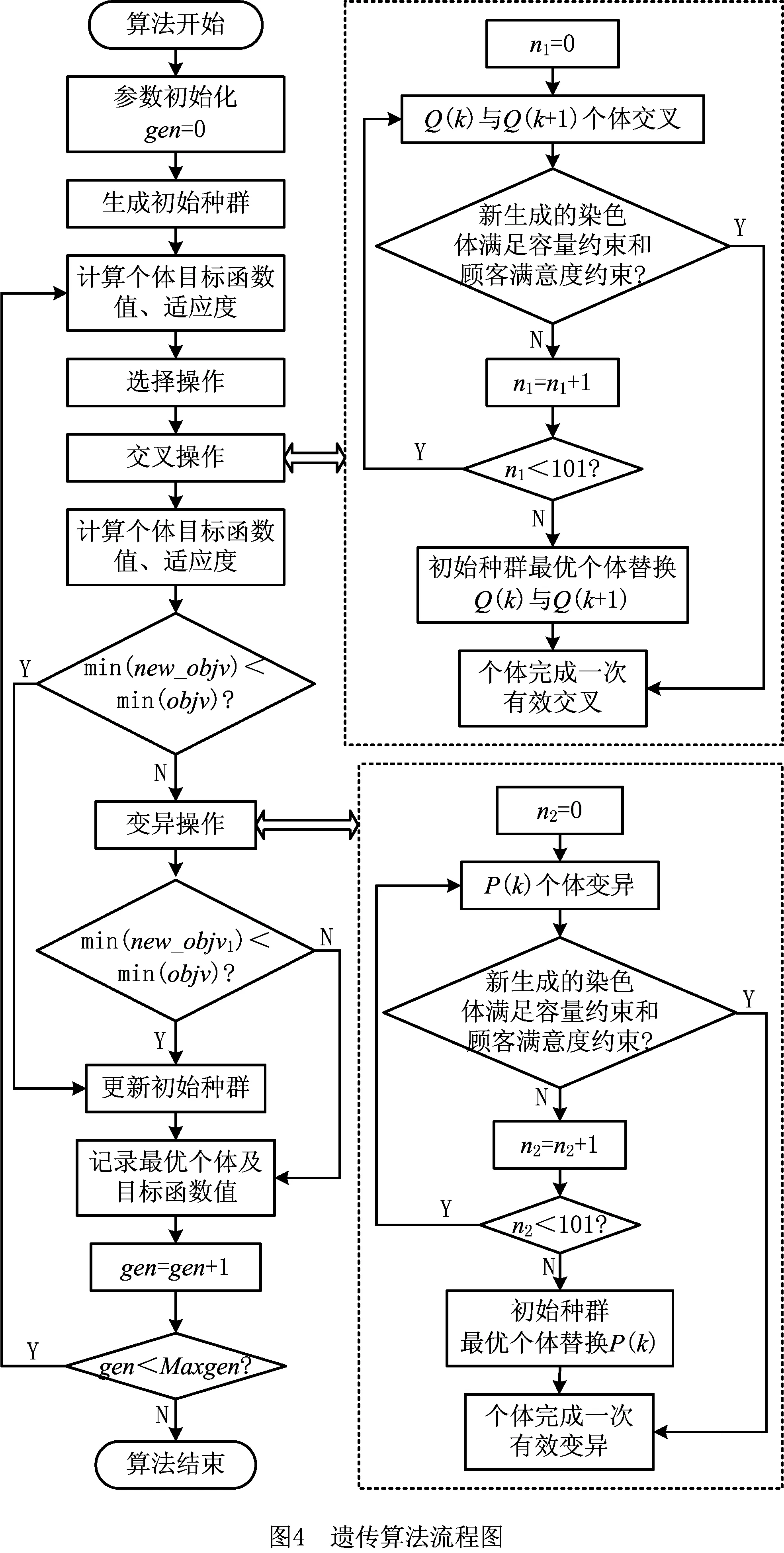
2 遗传算法设计


3 算例分析
3.1 算例描述

3.2 求解结果

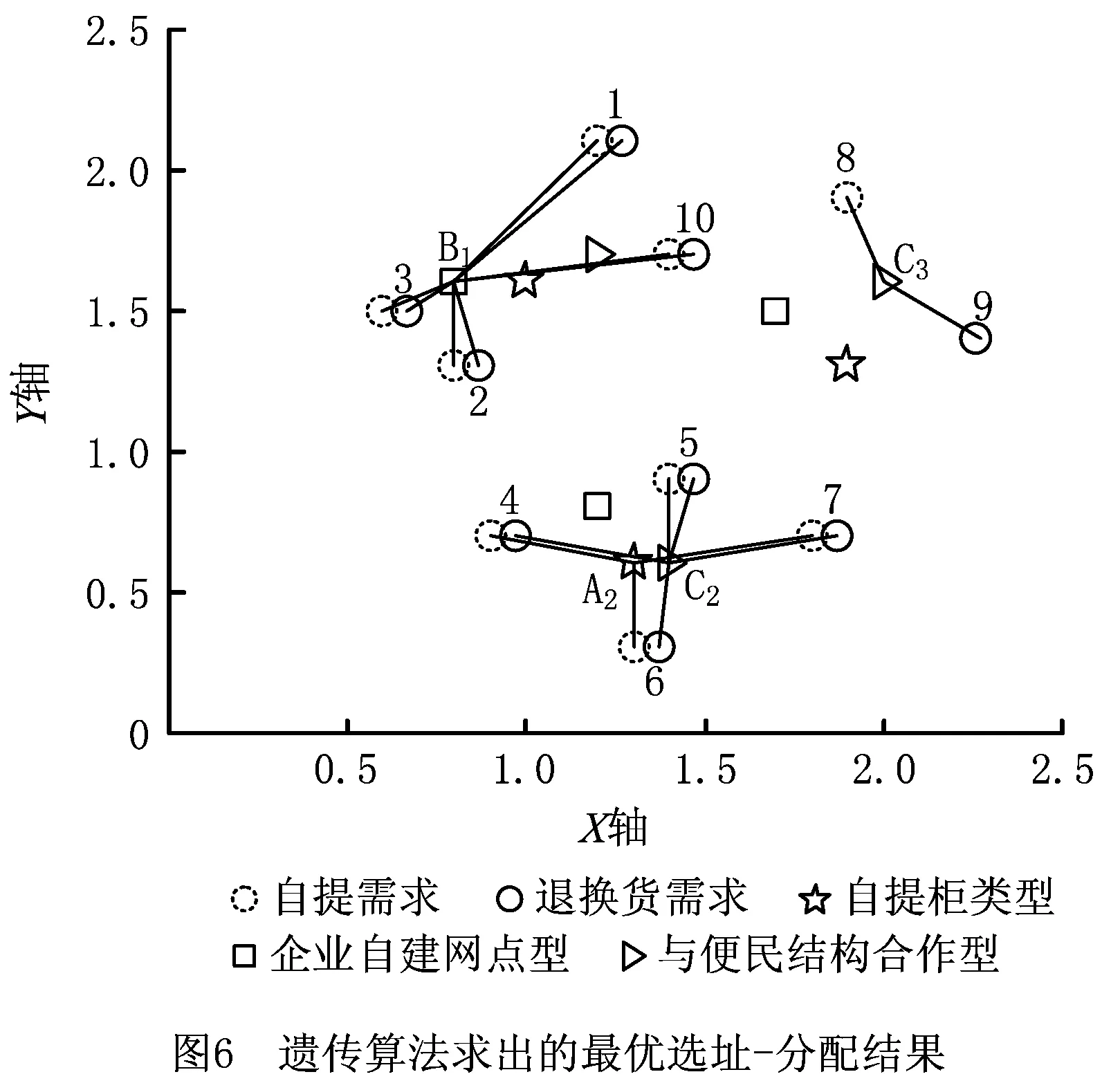
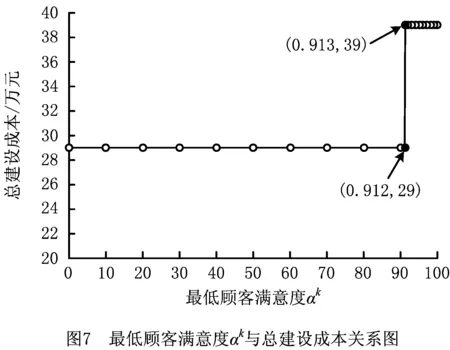
3.3 结果分析
4 结束语
