基于自抗扰控制的铣面机床电液位置伺服系统控制策略

徐莉萍，蔡留金+，李 健，胡东方，马昊依

(1.河南科技大学 机电工程学院，河南 洛阳 471003;2.河南科技大学 机械装备先进制造河南省协同创新中心，河南 洛阳 471003)

0 引言

铣面机床是精密铜管加工过程中不可或缺的加工装备，其主要功用是对管坯进行表层氧化皮铣削处理。铣面机床进行铣削加工的执行机构普遍采用电液伺服驱动，通过伺服缸活塞杆驱动铣刀运动实现铣削进给量的自动控制。然而，电液伺服系统具有参数时变、严重非线性及复杂负载干扰等特点，使得铣面机床铣削加工很难获得较高的加工精度和铜管表面光洁度，严重制约了铜管加工行业的发展，如何通过提高铣面机床电液伺服系统的位置控制精度,进而提高铜管表面加工精度已经成为了业内亟待解决的问题。

韩京清[8-9]于20世纪90年代提出的自抗扰控制(Active Disturbance Rejection Control，ADRC)技术是一种非线性鲁棒控制技术，该方法将所有作用在被控对象上的不确定因素统一归结为“未知扰动”，采用被控对象的输入输出数据对其进行估计后给予相应的补偿。ADRC以其良好的控制品质和独特的控制思想广泛应用于不确定性系统的估计和控制中。这种不依赖于系统具体数学模型的控制技术将铣面机床电液位置伺服系统控制中非线性、参数时变及负载扰动等不确定因素作为未知扰动，利用系统输入输出数据进行估计并给予相应的位置补偿，提高了系统的位置控制精度。高志强[10]随后提出线性自抗扰控制器，其参数整定方法较为简便，理论分析较简单，在一定程度上推动了ADRC控制技术的理论研究与工程应用，但是线性自抗扰控制器在参数效率、控制精度和系统响应速度等方面都逊色于非线性自抗扰控制器。郭栋等[11]针对电液力伺服系统设计了非线性ADRC控制器，有效提高了系统的抗干扰能力和力伺服精度;管志敏等[12]将非线性自抗扰技术应用在火电厂主汽温控制中，结果表明控制系统具有优良的动态性能和较强的外部扰动适应性;刘文江等[13]应用非线性自抗扰技术设计了船舶航迹控制器，取得了较好的系统动态特性和鲁棒性;刘善慧等[14]针对凹印机多色套准控制系统高精度高稳定性的控制要求，设计了基于非线性自抗扰技术的前馈控制器，有效抑制了各种内外扰动对套准误差的干扰，实现了高精度套准控制;高炳微等[15]、吕猛等[16]对电液位置伺服系统ADRC控制方法的应用进行了研究，得到了很好的控制效果，但仅限于仿真研究阶段。

鉴于此，本文针对铣面机床电液位置伺服系统的控制要求，提出一种基于ADRC的铣面机床电液位置伺服系统控制策略。根据该系统模型参数时变的特性，分别建立伺服阀控非对称伺服缸在活塞杆伸出和缩回时的数学模型，并推导出系统的传递函数；根据系统模型阶次设计非线性ADRC控制器，以实现参数时变和负载扰动下系统位置的精确控制；对系统在PID控制与ADRC下的控制特性进行了对比仿真分析，并进行了现场应用实验验证。

1 铣面机床电液位置伺服系统建模

铣面机床执行机构工作原理如图1所示，该系统主要由非对称伺服缸、电液伺服阀、伺服放大器、位移变送器、滑块、导轨和盘形铣刀等部件组成。工作时，通过伺服控制器改变电液伺服阀的阀口开度，控制非对称伺服缸活塞杆运动，再由活塞杆推动滑台沿导轨运动，进而改变盘状铣刀的位置以控制铜管的铣削厚度，非对称伺服缸活塞杆的位置通过位移变送器进行检测反馈。

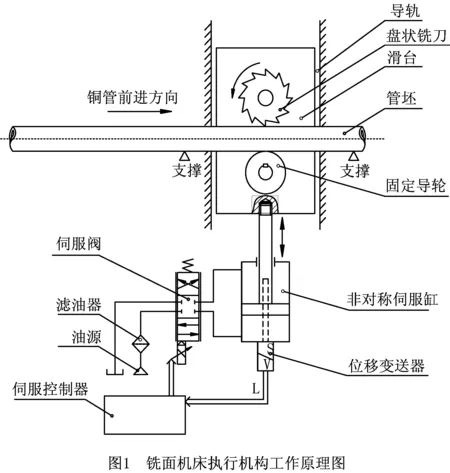
1.1 伺服阀控非对称伺服缸的流体动力学模型

铣面机床电液位置伺服系统的物理模型可简化为如图2所示的伺服阀控非对称伺服缸结构。非对称伺服缸结构的不对称性导致非对称伺服缸活塞杆在伸出和缩回时的运动特性不一致，因此必须分别进行建模研究。

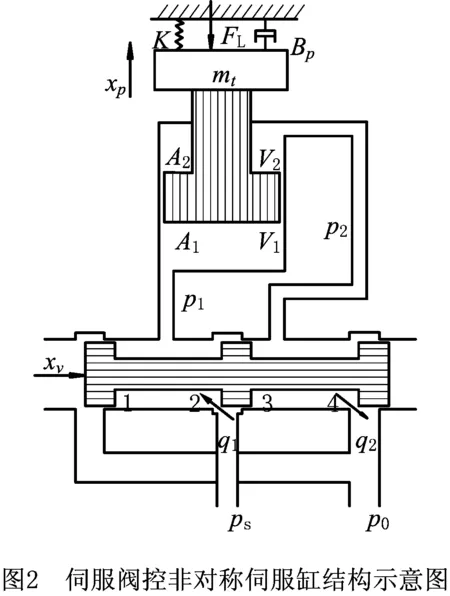
当伺服阀阀芯向右运动，即xv>0时，非对称伺服缸活塞杆伸出，此时伺服阀的流量方程[12]为：

(1)

式中：q1为非对称伺服缸无杆腔的流量；q2为非对称伺服缸有杆腔的流量；W为伺服阀各节流窗口的面积梯度；xv为伺服阀阀芯位移；Cd为伺服阀各节流窗口的流量系数；ρ为油液的密度；ps为供油压力；p1为非对称伺服缸无杆腔一侧的压力；p2为非对称伺服缸有杆腔一侧的压力。

负载流量可由式(1)得到：

(2)

式中：qL为负载流量；λ=A2/A1为流量比；A1为非对称伺服缸无杆腔的面积，A2为非对称伺服缸有杆腔的面积；pL=p1-p2为负载压力。

利用泰勒级数将式(2)线性化改造为

qL=Kqxv-KcpL。

(3)

式中：Kq为流量增益，Kc为流量-压力系数，且

(4)

根据流量连续性方程可获得非对称伺服缸的流量：

(5)

则负载流量可表示为

(6)

式(5)和式(6)中：xp为非对称伺服缸活塞杆的输出位移；Cip和Cep分别为非对称伺服缸的内、外泄漏系数；Ctp为总泄露系数，Ctp=Cip+Cep/2；βe为有效体积弹性模量；Ae为非对称伺服缸的平均活塞面积，Ae=(A1+A2)/2；V1和V2分别为非对称伺服缸进油腔、回油腔的体积；Ve为非对称伺服缸的等效体积，

(7)

式中：V为非对称伺服缸的最大体积，V=LA1；L为非对称伺服缸的最大行程。

根据负载和非对称伺服缸的受力平衡方程可得

(8)

式中：mt为活塞自身质量和折算到活塞上的负载质量的总和；K为负载弹簧刚度；Bp为活塞及负载的粘性阻尼系数；FL为作用在活塞上的任意外负载力。

1.2 铣面机床电液位置伺服系统的传递函数模型

将式(3)、式(6)和式(8)进行拉氏变换可得：

(9)

消去式(9)的中间变量QL(s)和PL(s)，可以求得非对称伺服缸活塞杆的总输出位移传递函数Xp(s)与阀芯输入位移XV(s)及外负载力FL(s)的关系：

(10)

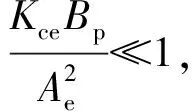
式中ωh和ξh分别为固有频率和阻尼比，

(12)

另外，伺服阀、放大器、位移变送器都可视为比例环节，且增益分别为Ksv，Ka，Kf。综上所述，建立xv>0时，铣面机电液位置伺服系统的闭环传递函数方框图，如图3所示。

同理，当伺服阀阀芯向左运动，即xv<0时，非对称伺服缸活塞杆缩回，得到非对称伺服缸活塞杆的总输出位移传递函数Xp′(s)与阀芯输入位移XV(s)及外负载力FL(s)的关系

(13)

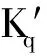
(14)

综合其他环节，可得xv<0时的铣面机床电液位置伺服系统闭环传递函数方框图，如图4所示。

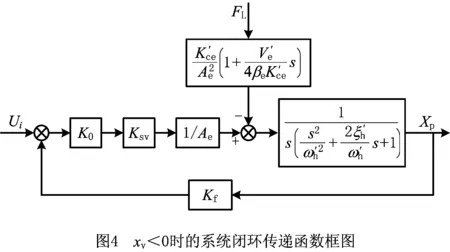
综上可知，在xv>0和xv<0两种工况下，虽然铣面机床电液位置伺服系统模型均是三阶的，但系统模型的参数发生了变化，说明铣面机床电液位置伺服系统是时变系统，这也是造成其控制精度不高的一个重要原因。

2 ADRC控制器设计

由铣面机床电液位置伺服系统的传递函数可知，该系统为三阶系统，根据其特点设计的ADRC控制器结构如图5所示。该控制器由1个三阶跟踪微分器(Tracking Differentiator，TD)、1个四阶非线性扩张状态观测器(NoLinear Extended State Observer，NLESO)、1个非线性状态误差反馈(NonLinear State Error Feedback，NLSEF)构成。其中：R为铣刀位置的指令信号；x1,x2,x3分别为位置指令信号R的安排信号、微分信号及二阶微分信号；z1，z2，z3为系统状态的估计值；z4为系统总扰动的估计值；e1，e2，e3为位置偏差信号；b0为补偿因子；u0为比较信号；u为控制信号；w(t)为干扰信号；y为输出信号。

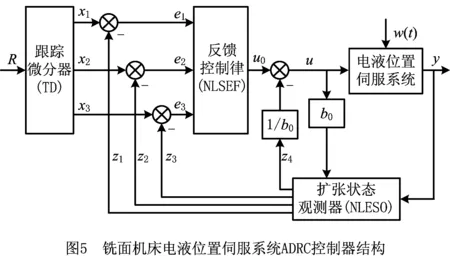
2.1 TD设计

TD的作用是安排过渡过程，给出铣刀位置指令信号R的微分信号，并产生参考指令信号的跟踪信号x1、一阶微分信号x2及二阶微分信号x3，可以减小因初始误差过大而产生的超调，有效缓解系统响应的快速性与超调之间的矛盾。所设计的三阶TD的离散算法为：

(15)

式中：r为速度因子，h为采样周期，h0为指令信号的滤波因子;fhan(x1,x2,r,h)为所设计的快速最优控制综合函数，具体算法如下：

(16)

2.2 NLESO设计

NLESO是ADRC的内核，其主要作用是观察铣面机床电液位置伺服系统各阶次的状态及内部和外部扰动，并给出相应的位置补偿量，以提高系统抑制内外扰动的能力。该系统的四阶NLESO离散算法为：

(17)

式中：β0i(i=1，2，3，4)为NLESO的增益系数，δ为线性段区间的长度，b0为补偿因子；fal(e,α,δ)的具体算法为：

(18)

2.3 NLSEF设计

NLSEF将过渡过程与估计的状态变量之间的偏差进行非线性组合，产生误差反馈控制量u0，用扰动估计值z4的补偿决定最终系统所需的控制量u，从而将铣面机床电液位置伺服控制系统由非线性系统转化为积分器串联型系统，实现了动态系统的反馈线性化。所设计NLSEF的离散算法为：

(19)

2.4 铣面机床电液位置伺服ADRC控制器的参数整定方法

参数选取是决定ADRC控制器控制性能的关键，但目前为止，ADRC控制器参数的整定尚没有成熟的理论指导，主要依靠实验方法确定。大量理论研究和仿真分析表明，ADRC控制器完全可以按照“分离式”原则设计，即分别相对独立地设计出TD，NLESO和NLSEF，最后组合成一个完整的ADRC控制器。这种设计原理概念清晰、参数整定方法较为简便，易于实现工程应用。

(1)TD在该ADRC控制器中的作用是跟踪铣刀位置指令信号R并给出一个微分信号，r的取值影响输出信号的位置跟踪精度和安排过渡过程时间，其值越大，过渡过程越短。h0影响输出信号的位置跟踪精度，初始时可以取h0与采样时间h相等。

(2)NLESO的4个增益系数β0i(i=1，2，3，4)在调试时应根据系统的输出并结合NLSEF进行设置。首先需要将NLSEF的初始参数值设置为较小的数，然后粗调NLESO的参数值，按照从小到大的顺序逐渐调整β01，并观察z1跟踪铣刀位置的效果；然后依次调整β02和β03，并观察z2和z3跟踪铣刀位置的效果；最后通过调整β04来实现NLESO对系统状态及干扰量的精确跟踪。然而，这4个参数的调整并非一蹴而就，在仿真和实验环节需要多次反复调整才能达到最佳效果。

(3)NLSEF在该ADRC控制器中的作用是产生一个非线性状态误差反馈控制律，增大β11可以放缓系统调节速度，反之则加快系统调节速度。然而加快系统调节速度会增大系统超调量，产生振荡，此时适当增大β12和β13可以有效抑制超调，减小系统振荡。

b0作为ADRC控制器一个较为特殊的参数，不仅与控制量u相关，还与NLESO的第4个状态变量联系紧密。b0的选值决定着系统总扰动估计值的变化区间，其取值的变化同时影响4个补偿分量z1，z2，z3，z4的大小。

3 仿真分析与现场应用验证

为了验证所设计ADRC控制器的控制品质，分别在ADRC和PID控制下对系统的控制性能进行了仿真分析和现场应用验证。铣面机床电液位置伺服系统的模型参数如表1所示。

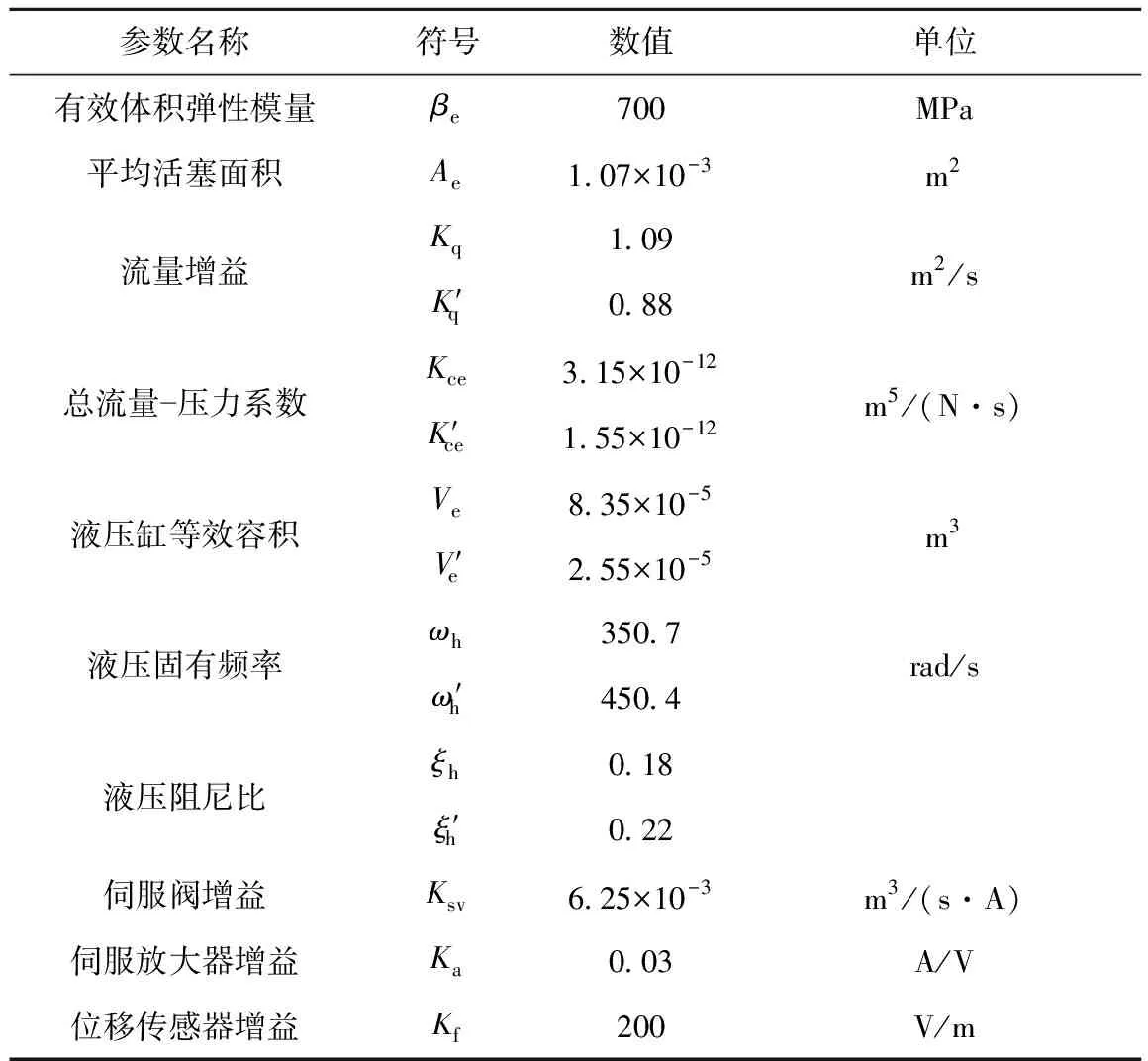
表1 模型参数

3.1 仿真分析

在Simulink中采用固定步长模式进行仿真，仿真步长和现场应用验证的采样周期保持一致，均为0.001 s。结合工业现场±0.2 mm的位置精度要求，设定仿真时系统的控制目标为在保证±0.1 mm位置精度的前提下尽可能减小系统响应时间和超调量。仿真过程中，在伺服缸伸出即xv>0状态下进行PID和ADRC控制器参数整定，反复调整后调定的PID控制器参数为kp=1.2，ki=20，kd=0.002；ADRC控制器参数为r=100，β01=4，β02=385，β03=39 760，β04=425 800，β11=55，β12=10，β13=2.8，b0=20，δ=2.6。

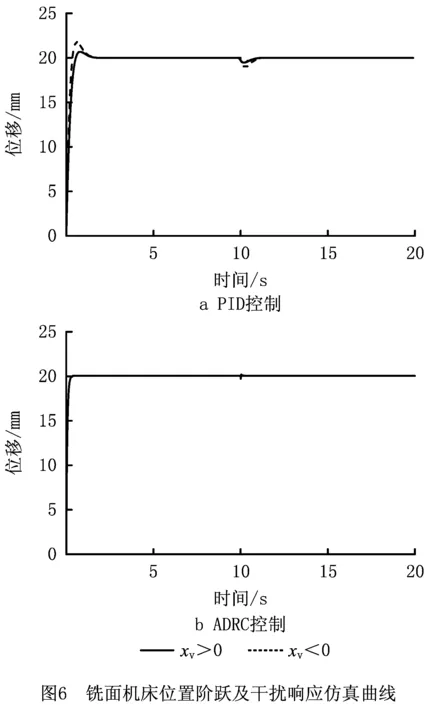
伺服缸在PID和ADRC控制下伸出和缩回时的阶跃响应，以及系统在第10 s时对负载施加1 000 N干扰时的响应曲线如图6所示。由仿真曲线可以得出：

(1)在ADRC控制条件下，系统稳态精度约为±0.06 mm，且系统的位置输出基本不受伺服缸伸出或缩回状态的影响，能够快速无超调地到达稳态值。而在PID控制条件下，系统在伺服缸伸出和缩回状态下表现出差异化的响应特性，具体表现为：液压缸伸出时，系统的上升时间tr=0.6 s、调整时间ts=1.6 s、超调量Mp=4%、稳态精度约为±0.08 mm；液压缸缩回时，系统的上升时间tr=0.4 s、调整时间ts=1.4 s、超调量Mp=8%、稳态精度约为±0.09 mm。这说明模型参数改变对ADRC控制器的控制效果影响不大，ADRC具有比PID控制更加良好的内部鲁棒性。

(2)虽然ADRC控制和PID控制都会在负载突变下产生控制误差，但是相同条件下ADRC控制下产生的误差无论在数值还是持续时间上都比PID控制下产生的误差小得多，例如液压缸伸出时，ADRC控制下负载突变的超调和持续时间分别为-1.4%和0.2 s，PID控制下负载突变的超调和持续时间分别为-4.8%和1.5 s。综合以上仿真分析可知，ADRC在铣面机床电液位置伺服系统控制中表现出了比PID控制更高的位置控制精度和更强的干扰抑制能力。

3.2 现场应用验证

为验证所设计控制策略的控制性能，在工业现场精密紫铜管铣面机床上进行了应用验证，实验设备如图7所示。其中油源为力士乐A10VSO28DFR/31R柱塞泵，实验供油压力为7 MPa；控制器采用针对铣面机床电液位置伺服系统自主开发设计的XC-28ML控制器，该控制器通过硬件RC低通滤波采样电路进行传感器数据采集，并将数据传输至STM32f107单片机中进行运算处理；伺服阀为中航工业FF102系列015221TP40电液伺服阀；位移变送器为康宇测控KYDM-LP1S2B10磁致伸缩位移变送器；伺服缸为天津优瑞纳斯UYS0511Q40/22-50HV。设定铣刀转速为2 500 r/min、铜管铸坯喂进速度为5 m/min、驱动铣刀旋转电机电流为20 A。实验过程中未长时出现电机电流过载，铣面机床运行较平稳。在伺服缸伸出即xv>0状态下进行PID和ADRC控制器参数整定，为了最大限度地满足工业现场±0.2 mm的铣刀位置控制精度要求，需要反复调整控制器参数值，最终调定的PID控制器参数为kp=1.5，ki=25，kd=0.002；ADRC控制器参数为r=100，β01=15，β02=523，β03=33 700，β04=463 200，β11=80，β12=16，β13=5.2，b0=20，δ=2.4。

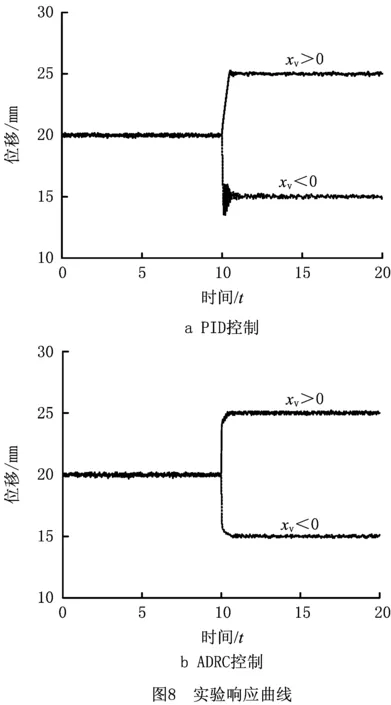
实验时，先使系统达到稳定的输出状态，然后为了验证系统抗干扰性能，在t=10 s时使伺服缸产生5 mm的阶跃伸出或缩回来模拟负载突变，铣面机电液位置伺服系统在PID控制下的响应曲线如图8a所示，在ADRC控制下的响应曲线如图8b所示。由图8a可以看出，调整好的PID控制参数在伺服缸稳态时的位置控制精度约为±0.15 mm，当位置阶跃变化5 mm时产生了切削力的负载扰动，无论液压缸伸出还是缩回系统都产生了较大超调，且伺服缸缩回时的超调量和调整时间明显比伺服缸伸出时大，说明PID控制不能很好地适应系统模型变化和负载扰动的影响。由图8b可以看出，在ADRC控制下，伺服缸在稳态时的位置控制精度约为±0.11 mm，且无论是伸出阶跃还是缩回阶跃，系统均能在较短时间内响应且不产生超调，说明ADRC具有较好的适应系统模型变化和抗外负载扰动的能力。对比图8a和图8b可以看出，ADRC控制无论在稳态精度还是动态响应方面都表现出了比PID控制更好的控制性能，说明ADRC控制策略具有比PID控制更好的内部鲁棒性和抑制外负载干扰的能力，有效保证了铜管表面质量和铣削厚度的均匀性。现场应用验证和仿真分析得出的结论基本一致，说明所设计的ADRC控制器在铣面机床电液位置伺服系统控制中能够取得较好的效果，验证了所提控制策略的有效性。

4 结束语

针对铣面机床电液位置伺服系统的特点和控制要求，本文依据流体动力学原理建立了阀控非对称缸的数学模型，并进一步结合伺服阀、伺服放大器、位移变送器等环节分别推导了铣面机床电液位置伺服系统在伺服缸伸出和缩回状态下的传递函数模型;依据系统模型的特点设计了三阶ADRC控制器，并对控制器的控制品质进行了仿真和现场应用验证。通过仿真和现场应用验证，得出以下结论：

(1)充分考虑伺服阀控非对称伺服缸系统中非对称缸结构不对称的特点，分别建立了非对称伺服缸在活塞杆伸出和缩回时的流体动力学模型，得到的数学模型更加贴近实际铣面机电液位置伺服系统，大大减小了模型误差，为系统的精确控制奠定了基础。

(2)利用ADRC技术在不确定性系统和多未知因素扰动系统中的独特控制优势，设计了基于ADRC的铣面机床电液位置伺服系统控制器，提高了系统在控制对象参数发生改变和外负载干扰作用下的位置控制精度，所设计的ADRC控制策略较PID控制具有更好的内部鲁棒性和抗干扰能力，更能适应铣面机床位置精确控制的要求。