高速列车齿轮箱箱体动应力响应及疲劳可靠性研究
2018-12-19王文静曲俊生李国栋戴晓超
王文静,张 莹,曲俊生,李国栋,戴晓超
(1.北京交通大学 载运工具先进制造与测控技术教育部重点实验室,北京 100044;2.中车长春轨道客车股份有限公司,吉林 长春 130062)
近年来,随着高速列车运营里程的增加以及运行速度的提高,以传动系统为代表的高速列车关键结构受到了广泛的关注[1-5]。齿轮箱驱动装置作为保证高速列车持续稳定运营的关键零部件和传动系统的重要设备之一,其结构安全性、稳定性、可靠性将直接影响着列车的正常运营。高速列车在武广、京沪、哈大运行时线路动应力试验结果表明[6-10],由于多种因素的影响,转向架构架、电机吊架、齿轮箱箱体、轴箱弹簧等部件的服役条件恶化,动态载荷增大,动应力响应增加。自2012年某高速列车发生第一起齿轮箱箱体疲劳裂纹故障以来,截至目前,箱体累计出现疲劳失效故障100余起[7]。因此,开展实际运用线路齿轮箱动应力响应影响及疲劳可靠性研究十分必要。
疲劳破坏是机械结构使用中重要的破坏形式之一,为了确保结构的安全可靠性,需对机械结构应力水平及损伤程度进行监测和评估。针对齿轮箱结构的应力响应特性及疲劳强度分析,KAHRAMAN、朱才朝、周志刚等[11-15]国内外学者做了大量的研究,但是这些研究主要集中在传统的机械领域,在铁路行业的分析研究并不多。目前对于高速列车齿轮箱结构的疲劳强度评估方法主要包含有限元仿真和线路试验法。在有限元仿真分析中,齿轮箱的载荷特点和约束条件均不能还原真实的服役环境,具有一定的局限性,而线路试验评估齿轮箱的疲劳强度则最为直接和有效。因此,本文以高速列车齿轮箱线路试验为基础,分析列车运行速度、电机输出扭矩及线路条件对箱体动应力响应及等效应力的影响规律,利用应力—强度干涉理论建立齿轮箱等效应力—疲劳强度干涉可靠性模型,分析齿轮箱箱体疲劳可靠度与列车服役里程的关系。研究结果可为齿轮箱结构的优化设计提供一定的理论参考和数据支撑。
1 试验方案
1.1 齿轮箱结构
齿轮箱是高速列车传动系统重要的组成部件之一,其结构主要由大小齿轮、上下箱体、轴承等部件组成。齿轮箱输出端通过轴承支撑在车轴上,输入端通过隔振橡胶、吊杆与转向架构架相连,上、下箱体材料为铸铝101A,其结构如图1所示。
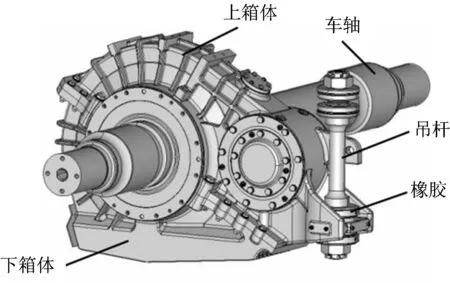
图1 高速列车齿轮箱示意图
1.2 线路动应力测试
为了确定高速列车齿轮箱箱体应力测点部位,需对箱体进行振动载荷和驱动扭矩组合工况下的应力分析,计算结果见图2。选取高应力位置布置应变片,测点见图3,其中测点1位于齿轮箱端部吊杆座。试验采用美国HBM公司生产的SoMateDAQ数据采集设备,可实现应力、加速度、GPS等信号的全程连续采集。试验分为大西(忻州西—原平西—阳曲西)型式试验以及武广、哈大正线运营试验。应力采样频率为2 500 Hz,可保证测试数据的有效性。
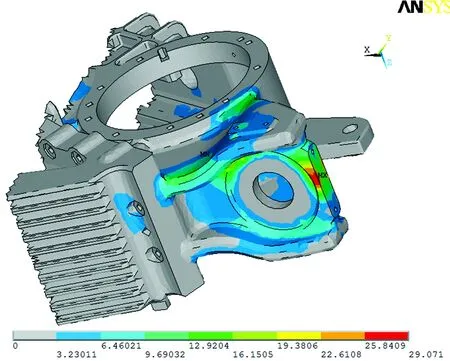
图2 齿轮箱应力计算结果
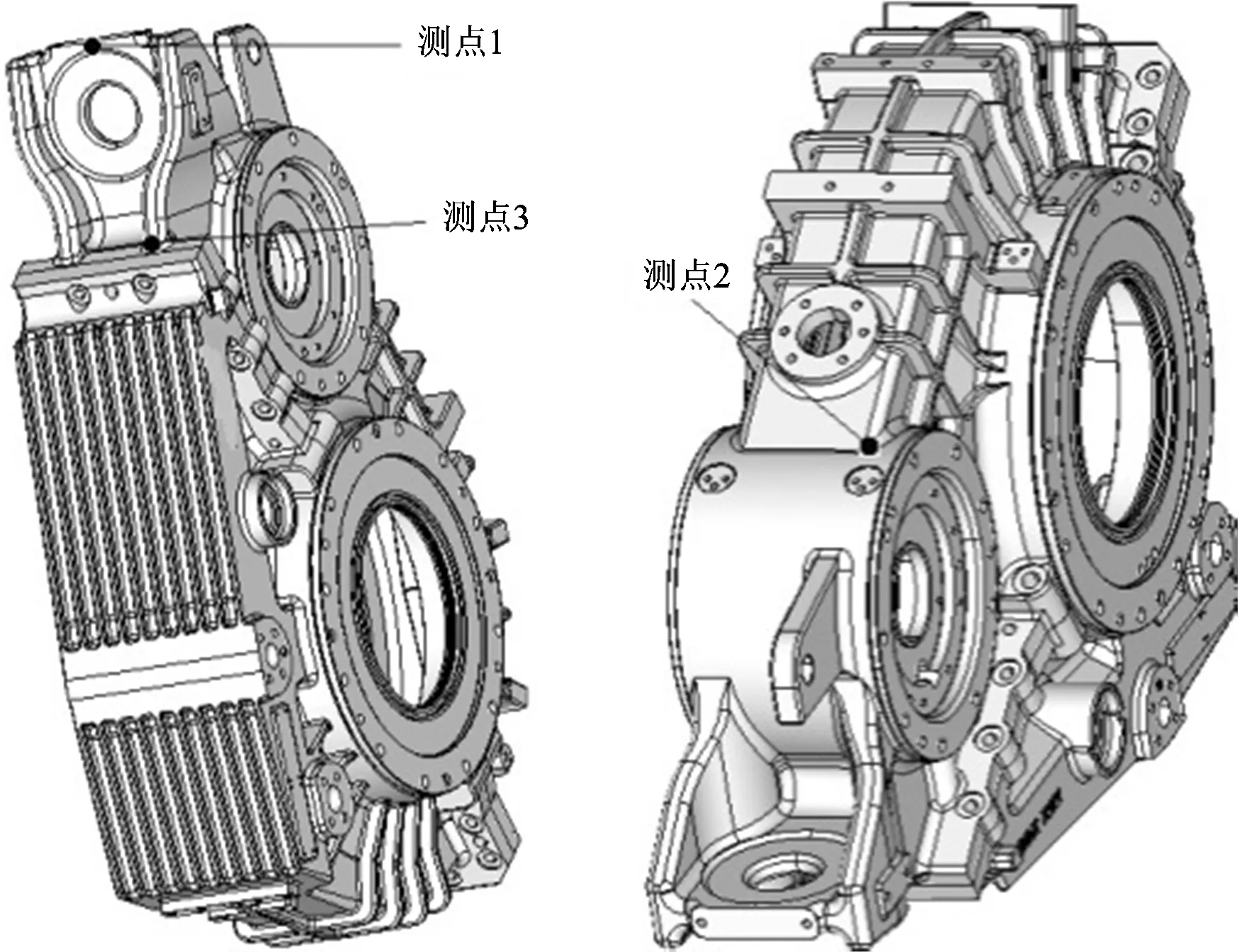
图3 测点布置示意图
2 等效应力计算方法
为了便于对变幅载荷下结构的动应力响应水平及疲劳强度进行评定,将应力幅值谱按损伤一致性原则等效为恒幅应力,即等效应力。该应力值可反映结构在一定工艺条件、运用工况和运用里程下的动应力状况。
根据Miner线性疲劳累积损伤法则和材料S—N曲线[16-17],推导出一个应力谱块的损伤公式如下
(1)
式中:D1为实测应力谱产生的损伤;C1为S—N曲线的参数;ni为各级应力水平对应的应力循环次数;m为S—N曲线的指数(文中取7.0)[18];σi为各级应力水平的幅值;Ni为对应于当前载荷水平的疲劳寿命;k为一个载荷谱的级数。
设等效应力σequ作用N次,结构损伤为D,则
(2)
式中:N为与材料疲劳极限对应的循环次数,取200万次。
已知运行L1的实测应力谱产生的损伤为D1,设在常幅载荷下运行L(结构寿命内的总里程,取1 200万km)产生的损伤为D,则
(3)
由式(1)—式(3)可得到等效应力σequ的计算公式为
(4)
3 箱体动应力响应影响因素
3.1 运行速度的影响
高速列车在线路运行时经历启动加速阶段、匀速运行阶段和制动减速阶段,其中以匀速运行阶段为主。因此,列车在匀速运行阶段的动态特性可代表列车系统的主要振动行为和特征。
试验测试了高速列车以时速为200,250,300,350 和400 km·h-1在新修线路(原平—阳曲)运行时齿轮箱箱体动应力响应时间历程。根据不同速度等级下齿轮箱体的动应力响应特点来分析列车运行速度对齿轮箱箱体应力水平及疲劳性能的影响程度。由于篇幅有限,本文仅给出了列车在客运专线某区段以时速为200和400 km·h-1运行时齿轮箱体测点1处的动应力响应时程曲线,如图4所示。可见,随着列车运行速度的增加,齿轮箱箱体动应力响应幅值水平也不断增大。当列车运行速度由200 km·h-1增加到400 km·h-1时,测点1处的最大应力幅值由6.83 MPa增大到14.98 MPa,增大约120%。
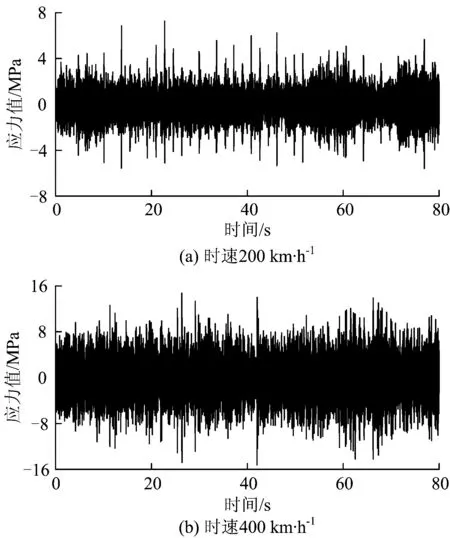
图4 动应力时间历程
为了进一步说明列车运行速度对齿轮箱箱体疲劳强度的影响,需分析不同速度等级下齿轮箱箱体的全程动应力时间历程,并利用公式(4)计算得到箱体不同位置处的等效应力值,计算结果如图5所示。由图可知,列车运行速度与箱体等效应力呈近似线性关系,箱体的应力水平随着列车速度的增大而增大,其中测点1处等效应力值最大。列车以时速400 km·h-1时测点1处的等效应力值可达20.7 MPa。
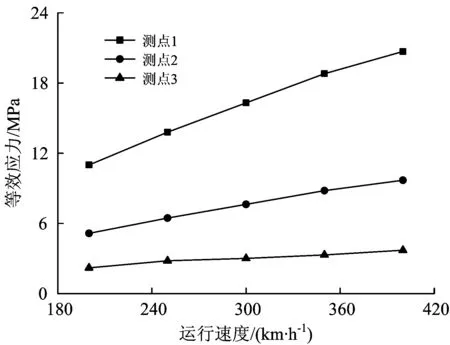
图5 等效应力与列车速度的关系
3.2 电机输出扭矩的影响
图6给出列车以时速300 km·h-1某线路区段运行时电机扭矩载荷的变化曲线。启动阶段电机输出扭矩在3 100 N·m波动,匀速运行阶段位于450~900 s之间。470~520 s时间段内电机输出扭矩在0值附近波动,列车处于惰性运行阶段,即电机无输出扭矩;730~810 s时间段内电机输出扭矩在1 400 N·m波动。试验线路为新修建线路,整条线路激扰无明显差异。
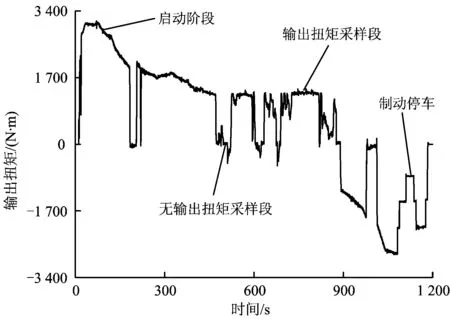
图6 电机输出扭矩变化曲线
图7给出了无电机输出扭矩和有电机输出扭矩阶段箱体测点1的动应力时间历程。由图可见,有电机输出扭矩时齿轮箱箱体动应力幅值水平高于无电机输出扭矩阶段,其动应力最大值分别为12.09,4.76 MPa。由此可知,列车电机输出扭矩对箱体动应力幅值水平具有较大的影响。
为了分析电机输出扭矩对齿轮箱箱体疲劳强度的影响,对全程动应力数据进行统计分析,得到有无电机输出扭矩条件下的动应力时间历程,并根据公式(4)计算了箱体不同测点处的等效应力值,其中电机输出扭矩阶段包含扭矩为800和1 400 N·m,计算结果如图8所示。从图中可以看出,随着电机输出扭矩的增大,箱体各测点处的等效应力值均有不同程度地增大,其中测点1的等效应力受电机扭矩的影响较为明显,800 N·m下的等效应力为16.04 MPa,1 400N·m下的等效应力为21.42 MPa。
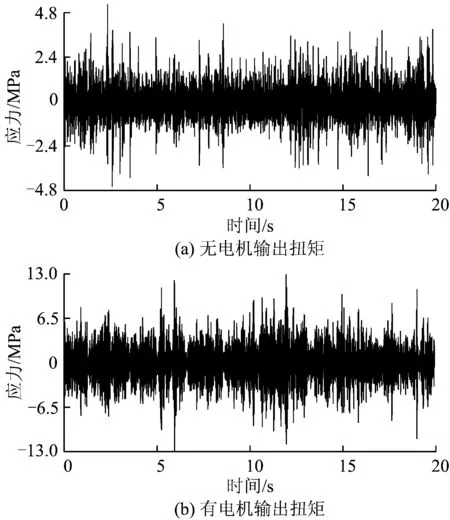
图7 动应力时间历程
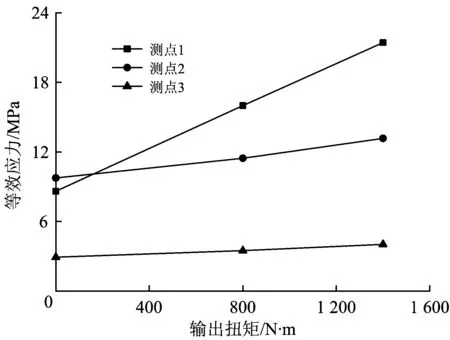
图8 等效应力与电机输出扭矩的关系
3.3 线路条件的影响
为探索线路条件对齿轮箱箱体动应力响应的影响,试验列车在哈大线(哈尔滨至大连)和武广线(武汉至广州)进行了测试。测试线路里程长、数据量大,本文随机抽取了齿轮箱测点1的动应力时间历程,如图9所示。从箱体动应力时间历程看,2种线路条件下的箱体动应力响应幅值无明显差异。
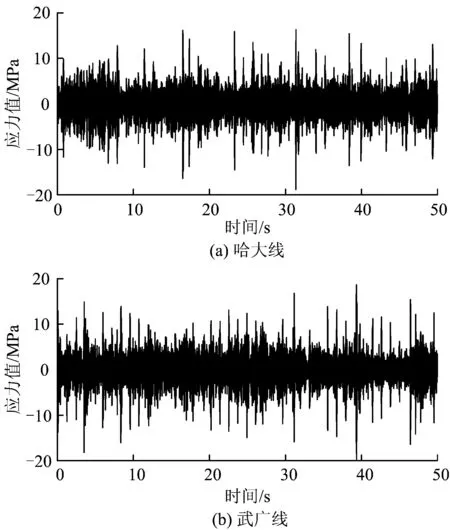
图9 动应力时间历程
采用公式(4)对全程往返数据处理并计算得到箱体测点1的等效应力值,其中10个往返的数据处理结果如图10所示。对图中2种线路条件下的等效应力值进行累加并求其平均值,这样可有效地降低随机误差的影响,使分析结果更为准确。当高速列车由哈大线转至武广线运行时,齿轮箱测点1的等效应力值由16.18 MPa增大到20.51 MPa,增大了27%。由此表明,高速列车在哈大线运行时的平稳性要高于武广线,哈大线的线路条件更为优良一些。
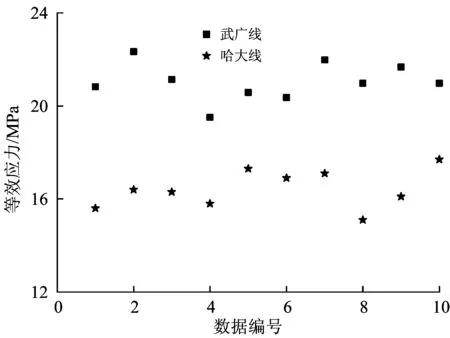
图10 等效应力与线路条件的关系
4 齿轮箱箱体疲劳可靠性
4.1 可靠性模型
应力—强度干涉理论广泛应用于机械结构件的可靠度分析[19],其基本原理是利用全概率公式计算结构应力小于疲劳强度的概率,即可靠度。齿轮箱箱体等效应力和疲劳强度均是独立的随机变量,具有分散性,且具有一定的分布规律。基于等效应力—疲劳强度干涉理论建立齿轮箱可靠性模型,其表达式为
(5)
式中:R为箱体疲劳可靠度;S为结构材料的疲劳强度;h(σe)和f(S)分别为等效应力、疲劳强度的概率密度函数。
当等效应力与疲劳强度均服从于正态分布时,结构可靠度可表达为
(6)
式中:μe和μS分别为等效应力和疲劳强度的均值;δe和δS分别为等效应力和疲劳强度的标准差。
统计分析动车组武广往返运行时箱体测点1的等效应力值,跟踪测试时间为90 d。图11给出了21组试验数据的处理结果,从图可以看出,等效应力的变化范围较小,离散度较低。
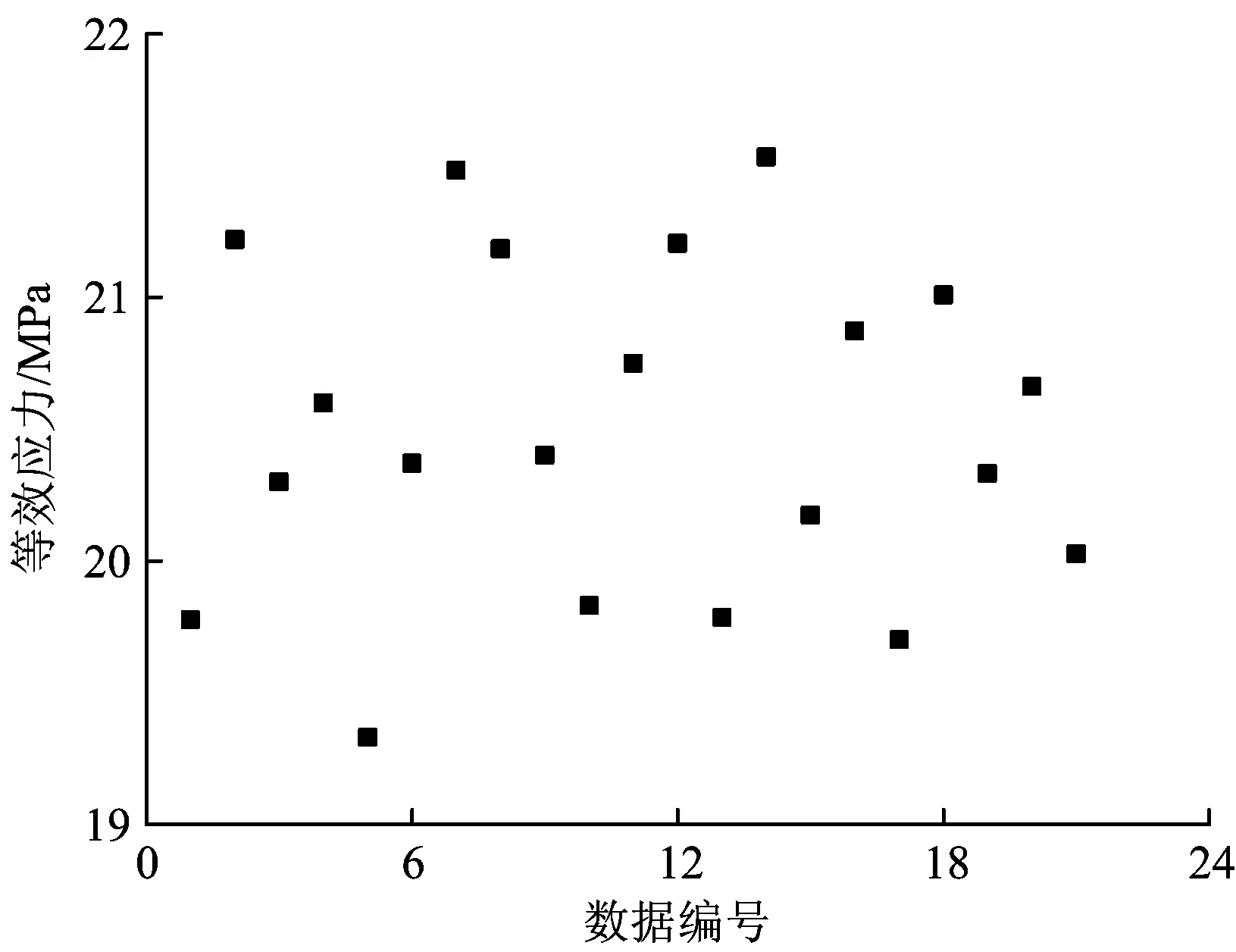
图11 等效应力离散图
假定应力传递系数服从正态分布,并利用Jarque-Bera检验法对样本进行假设检验,表达式为
(7)
式中:JB为统计量;n为样本容量;s为样本偏差;k为样本峰度。
若JB统计量的值超过临界检验值,则拒绝样本服从正态分布的假设,相反,则说明样本服从正态分布。采用JB假设检验法对图11中箱体等效应力进行正态分布检验可知,其JB统计值为0.88,小于检验临界值3.88,因此,统计得到的箱体等效应力服从正态分布。根据文献[18]中关于铸造铝合金疲劳强度的规定,铸造孔径为0.5和0.9 mm,选取循环次数为2×106时,其在可靠度为95%下的疲劳极限分别为25和20 MPa。选取变异系数为0.1,则铸造铝合金孔径为0.9 mm时疲劳强度的概率密度函数的表达式为
(8)
根据图11和公式(6)得到齿轮箱箱体的等效应力与疲劳强度干涉可靠性模型如图12所示。
4.2 疲劳可靠性
由公式(4)可知,等效应力的计算值与高速列车服役寿命L有关,当列车运行里程L发生变化时,箱体的等效应力也会随之发生变化。当列车服役里程为未知变量时,可得到等效应力公式为包含L的表达式,同样得到不同服役里程下的等效应力也服从于正态分布,且其变异系数为恒定值。
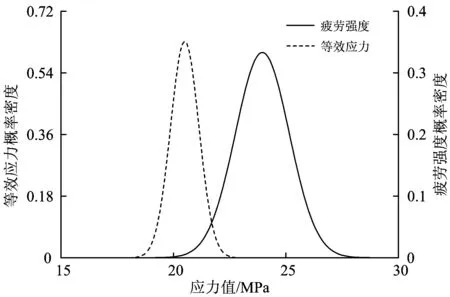
图12 等效应力—疲劳强度干涉可靠性模型
由此可以得到等效应力均值、标准差与列车运行里程之间的关系,如公式(9)所示,其中μ0,δ0为指定服役里程L0时箱体等效应力的均值和标准差。
(9)
式中:μeL和δeL分别为服役里程为L时箱体等效应力的均值和标准差。
根据公式(6)和公式(9)计算得到齿轮箱箱体疲劳可靠度与列车服役里程的变化关系,如图13所示。可见,随着列车服役里程的增大,箱体疲劳可靠度不断降低;在服役里程一定的条件下,随着铝合金铸造水平等级的提高,齿轮箱箱体疲劳可靠度呈现明显的增大。
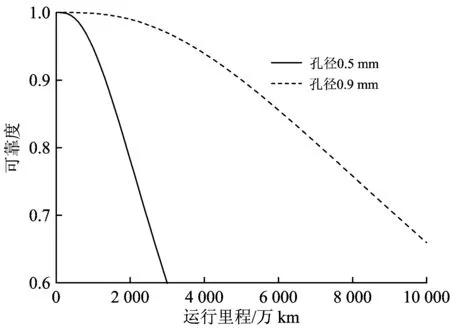
图13 箱体疲劳可靠度与服役里程的变化曲线
根据图13的分析结果,将不同疲劳可靠度下的齿轮箱箱体的服役里程列于表1。由表可知,随着可靠度的增大,箱体服役里程降低。在疲劳可靠度为95%时,铝合金铸造孔径为0.5 mm时的箱体服役里程是孔径为0.9 mm时的3.8倍。因此,在齿轮箱箱体铸造过程中应严格控制铸造等级,尤其在箱体结构的疲劳薄弱区,以免造成齿轮箱箱体的过早疲劳。

表1 齿轮箱箱体服役里程与可靠度、铸造质量的关系
5 结 论
本文以某新型高速列车齿轮箱为研究对象,分析了典型工况下箱体的动应力响应和疲劳可靠性,该研究可为齿轮箱箱体的优化设计和疲劳评估提供参考。
(1)随着列车运行速度的增加,箱体不同位置处的等效应力值均有不同程度的增加,且端部吊杆处的应力水平较高,当列车运行速度由200 km·h-1增加到400 km·h-1时,其最大应力幅值增大约120%。
(2)当列车以300 km·h-1运行时,有电机输出扭矩阶段的箱体动应力幅值高于无输出扭矩阶段,随着电机输出扭矩的增加,箱体各测点处的等效应力值均有不同程度地增大。
(3)线路条件对箱体应力水平有一定影响,高速列车在武广线运行时的齿轮箱箱体全程等效应力高于哈大线,端部吊杆座的应力高出约27%。
(4)齿轮箱箱体等效应力—疲劳强度干涉可靠性模型可直接反映箱体疲劳可靠度、铸造水平与服役里程之间的关系。分析结果表明:随着列车服役里程的增加,箱体疲劳可靠度不断降低;在一定可靠度下,随着铝合金箱体铸造水平等级的提高,齿轮箱箱体寿命明显增大,铸造孔径为0.5 mm时的服役里程是铸造孔径为0.9 mm时的3.8倍。
