基于不同工作区间的金属氧化物避雷器模型研究

， ， ，，

(1.国网安徽省电力公司 培训中心，合肥 230022； 2.国网江西省电力有限公司 电力调度控制中心，南昌 330001；3.国网重庆市电力公司 武隆供电分公司，重庆 武隆 408500)

0 引言

金属氧化物避雷器(MOSA)是一种用于雷电过电压和操作过电压的电力系统设备保护的设备。MOSA可以限制电力系统中设备遭受的过电压，防止绝缘失效。

MOSA具有良好的非线性特性(V-I曲线)。当它在正常运行条件下，流过MOSA的电流是毫安级别的；当它遭受雷电冲击时，在MOSA中可流过数百千安的电流。在这种电流的大区间内运行，每个工作区域内的MOSA都具有不同的电气特性[1-2]。

当MOSA在电力系统正常运行电压下工作时，它主要表现出电容性[3-4]。当MOSA遭受雷电冲击或者操作冲击时，它将工作在中间的高度非线性区，主要表现出电阻性[2,4]。当遭受雷电冲击或快速暂态过电压(VFTO)时，它工作在大电流区内，主要显现出电感性[5-9]。并且，MOSA的残压随着电流脉冲波头时间的减少而增加。因此，建立一个通用的模型来表示MOSA在大工作范围内的电气特性是非常复杂的工作。然而，目前的一些模型只适用于特定频率的研究，电力系统经常包含多种运行状况(正常，瞬态等)，所以现有的MOSA模型不能适用于所有工况[10-11]。

为了表示避雷器的3个工作区域，描述大范围内的V-I特性，本文提出了MOSA大范围(MWR)模型。提出的模型基于12个来自5个厂家生产的具有不同尺寸和电气性能的ZnO电阻片的测试数据。并且，将MWR模型的仿真结果与试验测试结果进行了比较，结果显示MWR模型在3个工作区内均能适用。

1 MOSA的V-I特性

MOSA的典型V-I特性曲线见图1[12]。V-I特性曲线来自一个线路放电等级为2级以及额定放电电流为10 kA的避雷器。

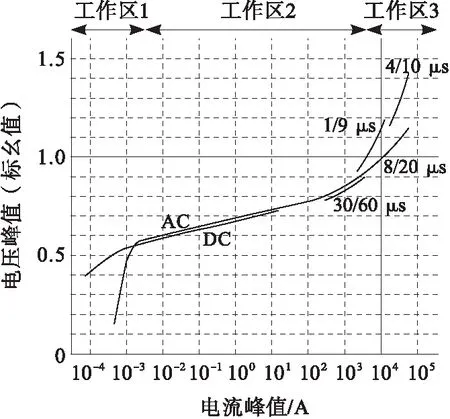
图1 幅值为10 kA线路放电等级为2级的ZnO避雷器V-I特性曲线Fig.1 V-I characteristics of a ZnO surge arrester with In=10 kA,line discharge class 2

工作区域1为泄漏电流区，MOSA工作在稳定状态。在这个区域内，电流密度[2]低于10-4A/cm2，V-I曲线近似为线性[2,4]，且与温度[13-14]和电容大小[2,4]有关。

工作区域2为中间非线性区，由于暂时过电压出现，MOSA开始工作。中间非线性区是MOSA的主要工作区域，在MOSA上流过的电流越大，那么在设备上产生的电压就越小。非线性度由非线性区的平滑度决定；在这个区域内，V-I曲线越平滑，设备就越安全[2]。MOSA在此区域内几乎是纯电阻性[2]。

工作区域3为大电流区，MOSA工作在雷电冲击的状态下。此时的电流密度大于103A/cm2。在此区域，观察到电压电流波形[5,7,8]的幅值更高，上升更快。

2 试验测试

使用了12个来自5个不同厂家生产的ZnO电阻片，根据它们的物理特性和电气特性进行分组。电阻片被标记为A,B,C,D,E和F，电阻片的相关参数见表1。

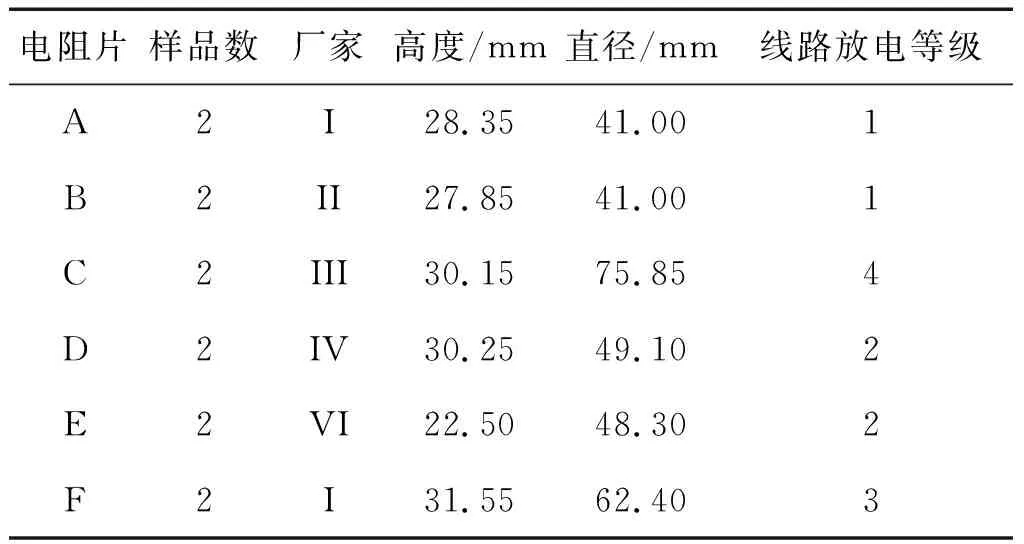
表1 ZnO电阻片的物理特性和线路放电等级Table 1 Physical characteristics and line discharge class of the ZnO varistors

通过在3个工作区域内进行电气试验，对电阻片进行评估，从而得到它们的整体特性。本文在试验中得到了电压和电流波形，将其用于电气模型的建立和验证。试验测试总体示意图见图2。该平台由电源(交流电、操作冲击电流和雷电流)，一个短路保护电阻(Rp)，一个高压探头(允许电压测量)，一个视电流电阻(CVR,测量通过电阻片的电流)，以及由数字示波器与计算机组成的数据采集系统组成。现场布置见图3。

图2 试验设置图Fig.2 Experimental set-up

为了建立在低电流工作区电阻片模型，在工频下进行了不同电压等级的试验，并记录了所施加的电压及其相应泄漏电流的波形。

(a)交流电源

(b)操作冲击和雷电冲击发生器

为了更好地表征电阻片在高度非线性和大电流的工作区域，需要评估试品和测量系统间的电感耦合程度。在技术标准[15-16]中，提出了一种方法来补偿由试验装置产生的感应电压。一般而言，补偿过程应用于陡电流脉冲残压的试验，但在本文的工作中，对操作冲击和雷电冲击都进行了补偿。

把相同尺寸的金属块(铝)和ZnO电阻片串联。当它们的电流脉冲波形和振幅相似时，分别在ZnO电阻片和金属块中测量残压。如果金属块上的峰值电压大于ZnO电阻片峰值电压的2%，那么就需要进行补偿，将金属块的脉冲形状从ZnO电阻片的脉冲形状中消除[15]。

因此，在开始特性试验之前，笔者对试验装置的感应电压进行了评估。为此，先对操作冲击电流发生器进行调整，产生波形30/60 μs，幅值分别为250 A，500 A，1 kA和2 kA的电流脉冲，再将脉冲施加到ZnO电阻片上。测量得到金属块上的峰值电压大于ZnO电阻片上残压峰值的3%。因此，在操作冲击电流的试验中，所有电阻片都得到了补偿。

为了表征MOSA在大电流工作区的特性，笔者在电阻片上施加了如下波形和幅值的脉冲电流：1.5/26 μs，3/6 μs，4/10 μs和8/20 μs；幅值为4 kA，8 kA，10 kA和15 kA。同样地，在电阻片试验开始前，进行补偿测试，测量得到金属块上的峰值电压达到了ZnO电阻片残压峰值的13%。因此，需要对残压中存在的感应电压进行补偿。如图4所示是在电阻片A1上施加8/20 μs-15 kA脉冲电流后得到的测量电压波形，金属块上的电压波形以及提出的补偿电压。

参考技术标准[15-16]，它考虑了由于电感引起的电压降，补偿后的电压降。本文在残压得到补偿后，还在模型上添加一个电感来表示由避雷器长度引起的电压降，见图5。

图4 电阻片A1和金属铝块的电压电流波形Fig.4 Voltage and current measurements in varistor A1 and aluminum block

图5 本文提出的电气模型Fig.5 Proposed electric model

3 避雷器数学模型

图5中电感L表征与流经MOSA的电流产生的磁场，它取决于MOSA的高度和ZnO电阻片内部并联的列数。电感L的计算参考文献[6,9]，它与高度的关系计为1 μH/m，最终其表达式见式(1)。电容C表征ZnO电阻片的介电常数，它取决于MOSA的高度，线路放电等级和ZnO电阻片内部并联列数。非线性电阻R(i)表示MOSA的导电能力，它取决于线路放电等级和经过MOSA的电流的脉冲波头时间。ATP仿真软件可用梯形积分法作为数值求解方法，则使用电阻RL和RC可用来避免数值振荡的情况发生。电阻值取决于仿真中设置的步长[17]。如果不使用梯形积分法则，则可以忽略电阻RL和RC。

确定MWR模型参数的步骤如下：

1)参数L和RL可从下式求得：

(1)

(2)

式中：h为MOSA的高度；n为ZnO电阻片内部并联的列数；Δt为仿真中的步长。

2)根据表2中ZnO电阻片的电容值与内部并联的列数n，MOSA的高度h和线路放电等级的关系以及通过试验测量的数据，可以获得参数C。根据文献[3]可进行电容C的估算，其值与避雷器高度和线路放电等级有关。

表2 ZnO电阻片的电容值与内部并联的列数n，MOSA的高度h和线路放电等级的关系Table 2 Capacitance of the MOSA as a function of the number n columns in parallel of ZnO varistors inside the MOSA,height h in meters,and line discharge class

3)参数Rc见式(3)[17]：

(3)

4)参数R(i)可通过表4的数据获得。这些数据是根据幅值为10 kA的雷电流冲击(8/20 μs)得到的残压峰值进行归一化处理获得。如果模型用来研究雷电冲击(8/20 μs)，操作冲击或低电流工作区域，这些数据点必须乘以标准雷电流冲击的残压峰值。另外，若需要用MWR模型来研究快速暂态过电压(VFTO)，例如0.5 μs的上升沿，V-I曲线的最后6个点必须乘以幅值为10 kA的VFTO残压峰值。最后，标记了*的数据点需要通过MOSA的线路放电等级进行调整，见表3。

表3 MWR模型在不同线路放电等级下在高度非线性工作区内的非线性电阻的V-I特性值的标幺值Table 3 V-I characteristics normalized of the MWR model nonlinear resistance,in the high nonlinearity region,in accordance with the line discharge class

本文给出了一个确定MWR模型参数的例子，见表4。

表4 WR模型非线性电阻V-I特征值的标幺值Table 4 V-I characteristic normalized of the MWR model nonlinear resistance

4 MWR模型特性分析

笔者利用ATP进行MWR模型的仿真。在信号采集的过程中对电压和电流信号进行了滤波，以降低噪声。为此，笔者使用了滑动平均滤波算法。

为了将仿真和测量的信号进行比较，使用了如下参数：

1)低电流工作区-泄漏电流的峰值和测量电流的R2统计。

2)高度非线性工作区和大电流工作区-残压峰值，测量得到的残压波形的R2统计，以及能量吸收值。

仿真中得到的峰值定义为Ps，试验测试中得到的峰值定义为Pm，两者之间的百分比误差定义为Pe，由式(4)给出：

(4)

为了比较能量的值，试验测试中的能量值(Em)和仿真中的能量值(Es)通过式(5)计算：

(5)

式中，v(t)和i(t)分别是残压和脉冲电流的瞬时值。式(6)可计算百分比误差：

(6)

最后，将从MWR模型得到的全部波形与试验测试得到的波形进行比较。为此，本文使用了R2统计。如果R2值接近于1，意味着所得模型的结果与试验数据能够很好吻合。R2统计方法由式(7)给出：

(7)

式中：

(8)

(9)

在低电流工作区内测量得到的信号波形见图6，以及MWR模型的仿真电流波形。这是当在电阻片上施加运行电压时，从电阻片F1中得到的具有代表性的结果。本文在每个需要评估的电阻片上均施加了4组不同等级的电压(在运行电压的10%～20%之间)，共48组试验。泄漏电流的绝对平均误差和R2统计见表5，值得注意的是R2统计值大于0.88，泄漏电流的峰值平均误差为3.66%。因此，MWR模型得到的泄漏电流波形较为准确。

图6 电阻片F1在低电流区内测量的电压电流波形以及MWR模型得出的波形结果Fig.6 Voltage and current measurements and provided by the MWR model in varistor F1 in the low current region

表5 低电流区的峰值电流的平均误差和R2统计Table 5 Average error in the current peak value and R2 statistic in the low current region

操作冲击电流脉冲(30/60 μs)波形，以及在幅值约为250 A和2 kA电流下的残压见图7。这些数据来自电阻片D1，并且本文给出了MWR模型的仿真结果。本文在其他电阻片上也通过验证得到了相同的特性。

图7 电阻片D1在高度非线性区内测量的电压电流波形以及MWR模型得出的波形结果(30/60 μs)Fig.7 Results of voltage and current easurements and provided by the MWR model in varistor D1,in the high nonlinearity region(30/60 μs)

在表6中，计算了6种不同类型的电阻片在高度非线性工作区的平均误差。对于不同类型的电阻片，残压峰值的整体平均误差低于1.8%；对于吸收能量的整体平均误差也非常低，低于3.1%。本文计算得到的R2统计值在0.51～0.91之间。因此，提出的MWR模型能够较好地在高度非线性工作区域反应ZnO电阻片特性。

表6 在高度非线性区内的电压峰值、吸收能量的平均误差和R2统计Table 6 Average error in the voltage peak value,energy absorbed and R2 statistic in the high nonlinearity region

图8显示的是雷电流脉冲波形(8/20 μs)、大电流脉冲波形(4/10 μs)和快速波前电流脉冲波形(1.5/26 μs和3/6 μs)，以及它们各自在电流幅值约为4 A和15 kA下的残压，以上的信号来自电阻片A1、B1、C1和E1上试验的测量值以及MWR模型的仿真结果。本文在其他电阻片的评估中也得到了类似的特性。

对于大电流区域，表7中所用的参数与表6相同。在本文中得到的残压峰值的整体平均误差低于2.2%；吸收能量的平均误差也很低，对于波形为8/20 μs,4/10 μs和3/6 μs的冲击电流，基本上都低于3%。然而，对于波形为1.5/26 μs的冲击电流，它的误差在4.9%～10.7%之间。这种情况发生的原因是MWR模型的阻尼不够精确，见图8(a)。但此时计算得到的R2统计值在0.61～0.90之间。综上，本文的MWR模型能够在大电流工作区较好地反应ZnO电阻片特性。

经过试验证明，在技术标准中提到的补偿过程不足以抵消试验设备对残压波形的干扰。因此，为了让模型和试验数据之间达到更好的效果，有必要人为地增加模型中的电感值。但增加电感值会失去电感L与避雷器高度(1μH/m)成正比的特点。对于此问题，一些研究采用了电磁耦合效应使对残压测量的影响最小化。

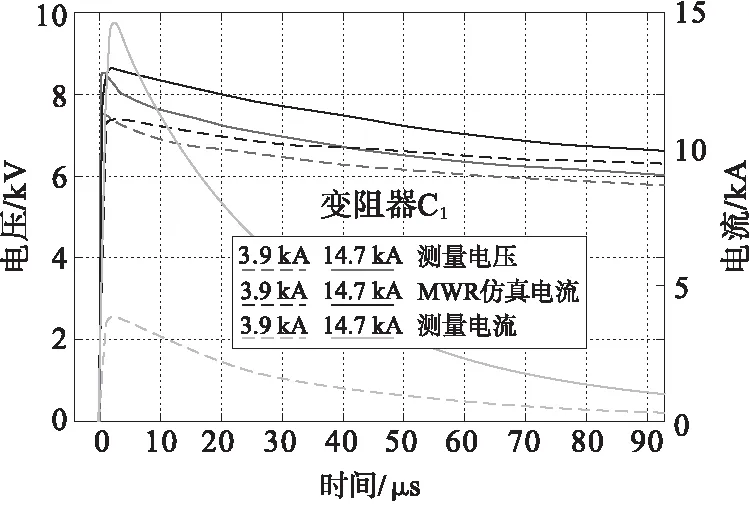
(a)电阻片C1-1.5/26 μs

(b)电阻片E1-3/6 μs

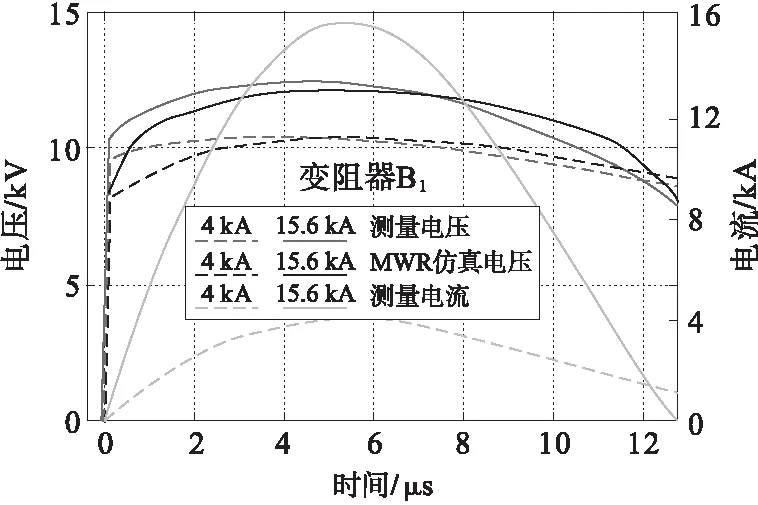
(c)电阻片B1-4/10 μs

(d)电阻片A1-8/20 μs

此外，本文提出的MWR模型能够很好地表示MOSA的特性，特别是它的性能/设计参数(电压电流波形，吸收能量)具有良好的精度(大部分结果的误差低于5%)。它可以用在各种运行情况下：工况、操作冲击和雷电冲击。

5 应用与实例

本节描述的是一个内部并联列数为1，线路放电等级为2级，全长为1.036 m的ZnO电阻片MWR模型参数的确定。幅值为10 kA，波形为8/20 μs的残压V10为192 kV；幅值为10 kA，波形为1/20 μs陡波的残压Vsp为206 kV。仿真中设置的步长为0.01 μs。

5.1 标准雷电波(8/20 μs)下MOSA在低电流区、高度非线性区和大电流区的模型

利用前面给出的方程，确定了L、RL、C和RC的值：

对于在幅值为10 kA，波形为8/20 μs，残压V10为192 kV的冲击波作用下得到的结果，将其乘以表4中电压(p.u.)的值可获得非线性电阻R(i)的V-I特性曲线上的点，结果见表8。为了更好地表示MOSA的电阻性，通过式(8)将V-I的特征点进行曲线拟合：

(10)

式中：i和v分别为MOSA的电流和电压；q为非线性系数；p为乘数因子；Vref为任意位置的参考电压。

5.2 对于特定雷电波形下MOSA在低电流工作区、高度非线性区和大电流区的模型

对于具有特定雷电波形电流脉冲的仿真，计算参数L、RL、C、RC的过程与前一种情况相同。在本文中只有V-I特性曲线上的最后6个点被修改，通过p.u.中的值乘以幅值为10 kA的特定雷电波的残压而得到，在此，特定雷电流波形为1/20 μs，残压Vsp为206 kV。

表8 MWR模型非线性电阻的V-I特性Table 8 Example of V-I characteristic of the mwr model nonlinear resistance

6 结论

提出了MOSA大范围模型(MWR模型)，该模型基于MOSA3个工作区域中的电气特性。通过对MOSA各个工作区域的电压和电流进行测量，验证了该模型的有效性。

通过MWR模型可以进行MOSA不同电气性能的研究。MWR模型可以避免当研究内容超过一个工作区域时，不同表示模型之间产生的误差。此外，MWR模型的使用方法简单，可在电力系统的仿真中长期使用。

本文提出的MWR模型仿真得到的电压或电流波形与试验测试的结果相似。在高度非线性区域和大电流区域中显现出的差异可以通过电感耦合的方法进行补偿。然而，在快速暂态的过程中，此补偿方法不够精确。

从测量结果来看，本文验证了在MOSA残压测量中使用电感耦合补偿法的正确性和重要性，例如在操作冲击电流波形(30/60 μs)中的应用。然而，与目前的一些技术标准不同的是，在快速暂态(波前时间小于等于1 μs)过程中使用补偿的方法具有一定局限性。