图形相似中的数学思想

文/于 涛 胡尊岩

数学思想是对数学内容进一步提炼和概括，是对数学内容的本质认识.下面把相似中常用的数学思想归纳如下.

一、方程思想

例 1 如图1，在△ABC中，EF∥BC，AB=3AE，若S四边形BCFE=16，则S△ABC=（ ）.

A.16 B．18 C．20 D．24

解析：∵EF∥BC，∴△AEF∽△ABC，

∵AB=3AE，∴ AE∶AB=1∶3，

∴S△AEF∶S△ABC=1∶9，

设S△AEF=x，

∵S四边形BCFE=16，∴，

图1

解得x=2，∴S△ABC=18. 选B．

二、分类讨论思想

例2如图2，△ABC中，∠ACB=90°，，AC=12，将△ABC绕点C顺时针旋转90°得到△A′B′C，P为线段A′B′上的动点，以点P为圆心，PA′长为半径作⊙P，当⊙P与△ABC的边相切时，⊙P的半径为_____．

解析：如图2，当⊙P与直线AC相切于点Q时，连接PQ．

图2

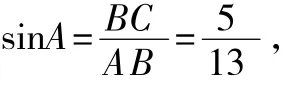
设BC=5x，则AB=13x，

∴AB2-BC2=AC2，

（13x）2-（5x）2=122，

∴x=1，

∴AB=13，BC=5.

设PQ=PA′=r，

∵PQ∥CA′，

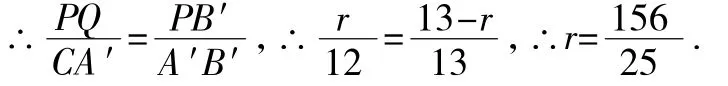
如图3，当⊙P与AB相切于点T时，易证A′，B′，T共线，

∵△A′BT∽△ABC，

图3

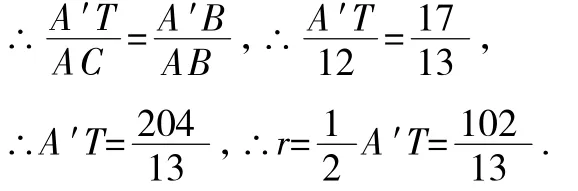
三、数形结合思想

例3为了测量竖直旗杆AB的高度，某综合实践小组在地面D处竖直放置标杆CD，并在地面上水平放置平面镜E，使得B，E，D在同一水平线上，如图4所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A（此时∠AEB=∠FED），测得旗杆顶A的仰角为39.3°，平面镜E的俯角为45°，FD=1.8米，问旗杆AB的高度约为多少米？（结果保留整数）（参考数据：tan39.3°≈0.82，tan84.3°≈10.02）

解析：如图4，∵FM//BD，

∴∠FED=∠MFE=45°，

∵∠DEF=∠BEA，∴∠AEB=45°，∴∠FEA=90°，

∵∠FDE=∠ABE=90°，∴△FDE∽△ABE，

图4

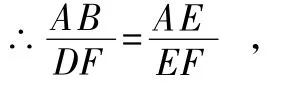
在Rt△FEA中，∠AFE=∠MFE+∠MFA=45°+39.3°=84.3°，tan84.3°=，，∴AB=1.8×10.02≈18.

四、转化思想

例4如图5，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（ ）.

图5

解析：∵DE∥BC，

选C．

五、函数思想

例 5如图6，在Rt△ABC中，∠A=90°，AB=8，AC=6．若动点D从点B出发，沿线段BA运动到点A为止，运动速度为每秒2个单位长度．过点D作DE∥BC交AC于点E，设动点D运动的时间为x秒，AE的长为y．

（1）求y关于x的函数关系式，并写出自变量x的取值范围；

（2）求△BDE的面积S与x之间的函数关系式；

（3）当x为何值时，△BDE的面积S有最大值，最大值为多少？

解析：（1）∵DE∥BC，∴△ADE∽△ABC，

∴当x=2时，S有最大值，且最大值为6．

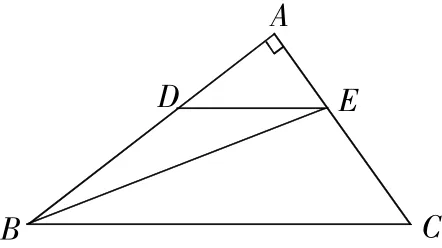
图6