多孔均质含水层中激发强度对微水试验结果的影响
2018-12-13万伟锋李清波蔡金龙
万伟锋,李清波,蔡金龙,曾 峰
(1.黄河勘测规划设计有限公司博士后科研工作站,河南 郑州 450003;2.黄河勘测规划设计有限公司岩土工程事业部,河南 郑州 450003)
微水试验(slug test)是一种简便且相对快速测定水文地质参数的野外试验方法,它起源于国外,其译名各异,如重锤试验、钻孔振荡试验、冲击试验、定容积瞬时抽(注)水试验等[1]。与传统试验相比,微水试验不仅更简便、经济,而且精度高,可以满足实际岩土体渗透参数测定的需要,同时,试验不会对地下水环境产生二次污染[2]。微水试验在国外研究较早,20世纪50年代,Hvorslev等学者首次应用微水试验对土体的渗透系数进行现场测定,并开发了相应的数学模型用于求解[3]。此后,许多专家学者致力于微水试验理论研究,针对不同含水层性质和水文地质条件,建立了不同的理论和数学模型,比较常用的除Hvorslev模型外,还有CBP模型、Bouwer-Rice模型、Kipp模型等,并对这些求解模型和方法不断进行改进和修正。
国内微水试验研究比国外开始的晚,国内最早研究微水试验的是长春地质学院(现吉林大学)水工系干旱半干旱水文地质研究室,在1979年提出了用瞬时抽水试验测定水文地质参数的方法[4],对其理论模型和求解方法进行了推导,此后的20年间研究热度较低;2000年以后,随着微水试验在工程中的应用,研究成果逐渐增多,如季纯波等推导了专门应用于潜水井裸井的微水试验数学模型[5],高彬等开展了花管与潜水面相交下的微水试验模型研究[6],赵燕容建立了不同倾角的室内裂隙物理模型,并修正了Kipp模型提出的标准曲线[7]。周志芳等提出了基于单孔分段振荡式微水试验确定岩体渗透系数张量和裂隙贮水率的计算模式[8]。到目前为止,国内外微水试验的求解模型和方法达50种之多。这些模型中,从多孔均质的承压微水试验理论模型发展到潜水微水试验模型,从不考虑瞬间水位变化的惯性效应指数衰减到考虑惯性效应的欠阻尼衰减,并发展到考虑井壁效应的理论模型,近些年一些学者开始从多孔均质介质逐渐转向裂隙岩体的研究[2]。微水试验在理论和求解方法方面已较为成熟。
在应用方面,微水试验很早就被作为一种原位试验方法广泛应用于水文地质、环境地质等领域的岩土体参数的测试中,并有相应的标准和规范。在国际上流行的含水层求参软件Aquifer Test中,有专门的微水试验求参模块。在国内,也有科研机构和生产单位研发的专门用于微水试验的设备,并在实际中进行了一些工程应用,和其他试验方法进行了对比研究[9~11]。在国内的一些教材、手册和规程中,微水试验已被列为水文地质试验之一[12~13]。
纵观微水试验的研究历程和成果,多集中在理论模型建立与改进、求解方法及其在实际工程勘察中应用等方面,对试验具体过程、方法及研究较少,不同激发方式的激发水头或激发强度对试验结果的影响鲜有报道,在实际工程应用中对试验水头尚无统一和明确的要求或标准。本文通过室内物理模型试验,模拟不同的激发方式下不同激发强度的微水试验,分析激发强度对试验结果的影响,以期获取微水试验较为适宜的激发强度,为今后微水试验在实际工程勘察中的应用提供借鉴和参考。
1 微水试验基本原理和常用激发方式
1.1 微水试验基本原理
微水试验的实质是通过一定激发手段(如瞬时抽水或注水、气压泵、振荡棒等)使得井孔内水位发生瞬时变化,通过观测和记录钻孔水位随时间的动态变化数据,并与相应的理论数学模型的标准曲线拟合,进而计算试验孔附近的水文地质参数。根据试验过程,又可分为降水头微水试验(使水位瞬时上升,然后记录水位下降恢复)和升水头微水试验(使孔内水位瞬时下降,然后等待水位上升恢复),见图1。
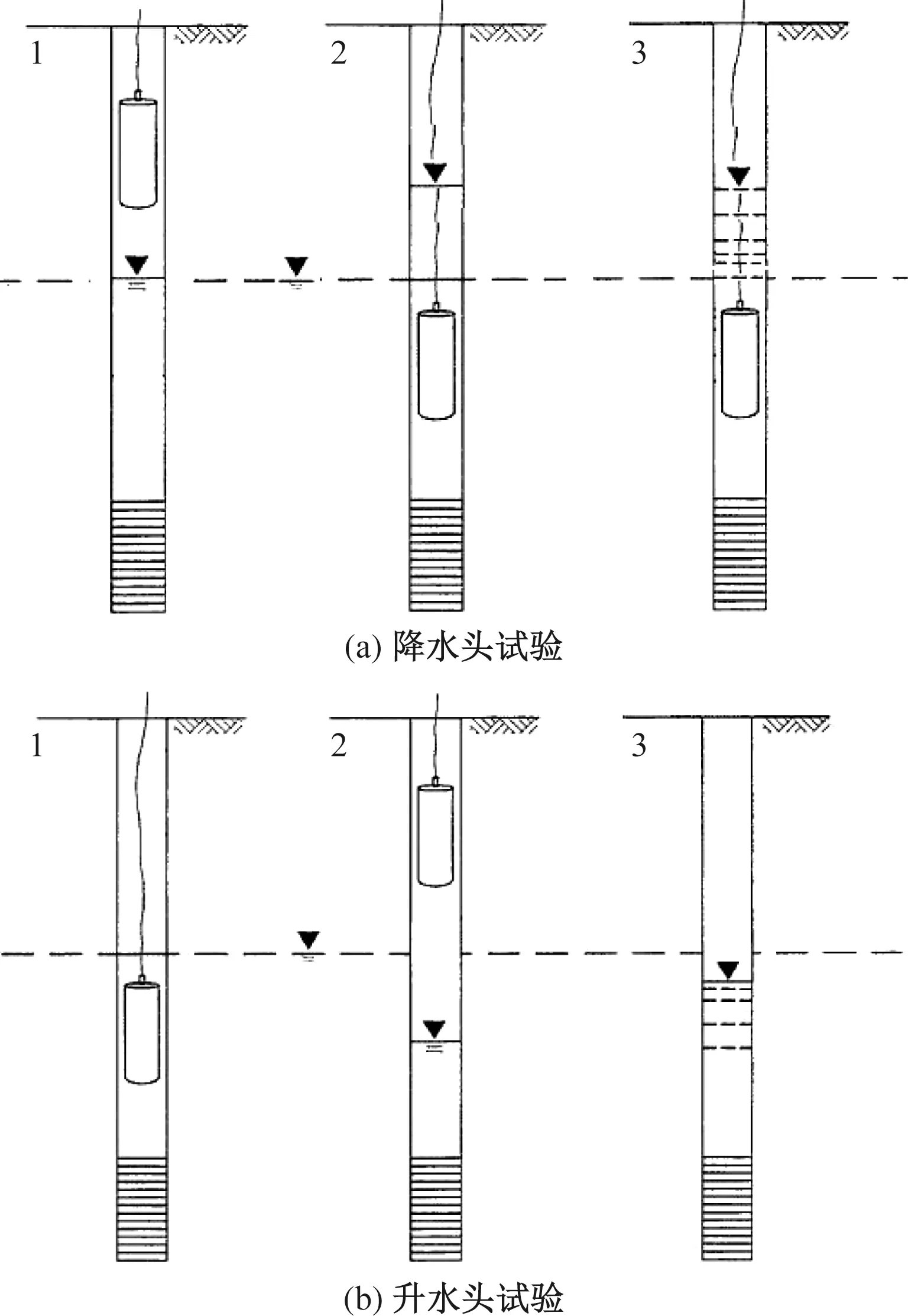
图1 微水试验过程示意图Fig.1 Schematic diagram of the slug test process
1.2 微水试验常用激发方式
为了使井、孔内的地下水位快速上升或者下降一定值,微水试验常用以下几种激发方式:
(1)注水式
注水式微水试验是快速向井、孔内注入一定体积的水,以达到使孔内的地下水位瞬间上升的目的,然后观测地下水位的恢复曲线,激发的强度基本可根据实际情况由人为注入的水量大小控制。注水式微水试验类似于降水头注水试验。
(2)提水式
提水式微水试验和注水式微水试验的激发形式相反,是从孔内瞬间提出一定体积的水,以达到孔内的地下水位瞬间下降的目的。试验激发的强度基本由提水器的容积确定。
(3)冲击式(也称沉入或提出重物式、震荡棒式)
通过沉入或者从孔内水位以下提出一定体积的重物是实际工作中较为常用的一种激发方式,一些文献中也称这种方式为冲击式或震荡棒式[7],其激发方式见图1,其沉入过程(升水头过程)类似于注水式微水试验,待其水位恢复后,提出过程(降水头过程)类似于提水式微水试验,所不同的是,由于重物(或称震荡棒)的体积是一定的,其激发的水头上升或者下降的幅度也是一定的,只能通过更换不同体积的重物(或称震荡棒)来改变激发强度。这种激发方式的优点是不需要用水、用电,可以很容易地实现水位瞬间上升、水位瞬间下降的两种类型的微水试验,并且可以将两种类型的试验进行对比分析,以相互验证试验结果。
(4)瞬间抽水式
瞬间抽水式微水试验是通过抽水设备从井、孔内在极短时间内抽取出一定体积的水,以达到井、孔内水位快速下降的目的,也称为快速抽水试验法。这种方法的激发强度主要靠抽水设备功率大小和抽水时间长短来确定,但需要注意的是,由于微水试验强调水位的快速变化,抽水应控制在较短时间内完成。
(5)气压式
气压式微水试验是通过对钻孔孔口进行密封,通过气泵向孔内加压,利用气压使孔内地下水位下降一定幅度,然后打开孔口排气阀门瞬间释放孔内压力,观测水位恢复过程曲线求取水文地质参数的一种微水试验。该方法也称为钻孔震荡式渗透试验或钻孔自由震荡法试验,在《水电水利工程钻孔抽水试验规程(DL/T 5213—2005)》的附录C中[13],有关于该方法的详细操作过程和技术要求。由于靠气压改变孔内水位,这种方法激发的水位变化值有限,一般在数厘米到数十厘米不等。
2 微水试验物理模型平台
2.1 试验平台概况
微水试验的物理模型外部由墙体四面合围,墙体厚度38~40 cm,内部形成4 m×4 m的正方形池子,池子四周及底部均做防水处理,外围墙体高度为2.2 m。基于地下水动力学的裘布衣圆岛理论的假设,以及微水试验理论的假设条件,将池内的孔隙含水层设置为圆形,圆形含水层模型的直径为3.8 m,距离水池四周墙壁最近约10 cm,圆形周边采用钢筋骨架+钢丝网+尼龙滤网进行固定。含水介质采用颗粒级配均匀水洗中细砂,砂层铺设厚度为1.5 m,均匀铺设完成后,经3次反复饱水、释水使其自由密实。
本次模拟的是潜水含水层,含水层厚度为1.3 m,通过模型侧壁上距离底部1.3 m处的溢水孔实现含水层边界处水位的稳定,模型示意图见图2。

图2 物理模型示意图Fig.2 Schematic diagram of the physical model
试验平台中心设置试验主孔,在两个相互垂直方向上不同距离设置了8个观测孔,以观测微水试验的影响范围和程度。为分析微水试验在不同孔径的钻孔中的适用性,物理模型试验考虑了3种主孔孔径,分别是110 mm、160 mm和200 mm。
2.2 微水试验类型
本次开展了注水式、提水式、瞬间抽水式和气压式4种类型的微水试验,其中注水式20组,提水式19组,瞬间抽水式14组,冲击式9组,气压式11组。由于气压式微水试验孔口封闭装置要求较高,仅在110 mm孔径中进行。
3 试验结果分析
3.1 求解方法
潜水含水层微水试验通常采用Bouwer-Rice模型进行计算,Bouwer-Rice模型适用条件是:非承压含水层,均质各向异性多孔介质,定水头有限直径圆岛形边界条件,忽略含水介质的弹性储水效应,即Ss=0。其几何模型见图3。
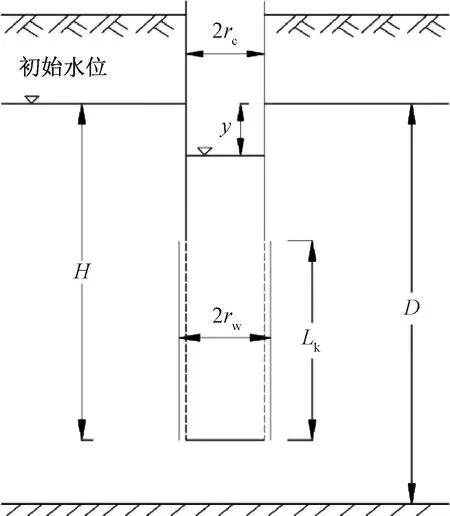
图3 Bouwer-Rice几何模型Fig.3 The Bouwer-Rice geometric model
Bouwer and Rice推导得到渗透系数K的表达式为:
式中:y0——钻孔中的最大水位变化值/m;
yt——t时刻钻孔中水位和初始水位的差值/m;
t——时间/s;
Re——试验影响半径/m;
rw——过滤管半径/m;
rc——钻孔套管半径/m;
Kr——含水层径向渗透系数/(m·s-1);
Lk——试验段滤管长度/m。
对于ln(Re/rw)的计算,在给定井孔和含水层几何特性如rw、H、D的条件下,注水流量Qt与Lk呈线性关系,Bouwer和 Rice通过试验研究得到与井孔和含水层几何特性相关的经验公式,该模型一般可以通过直线图解法求解,本次直接利用国际上流行的含水层试验软件Aquifer Test进行求解,该软件中包含微水试验模块,且有多种微水试验模型可以选择。
3.2 试验结果分析
不同试验孔径的微水试验结果见表1~表3,表中列出了各组试验的水头激发高度。表中,高度激发强度用激发水头高度占含水层厚度的百分比表示。
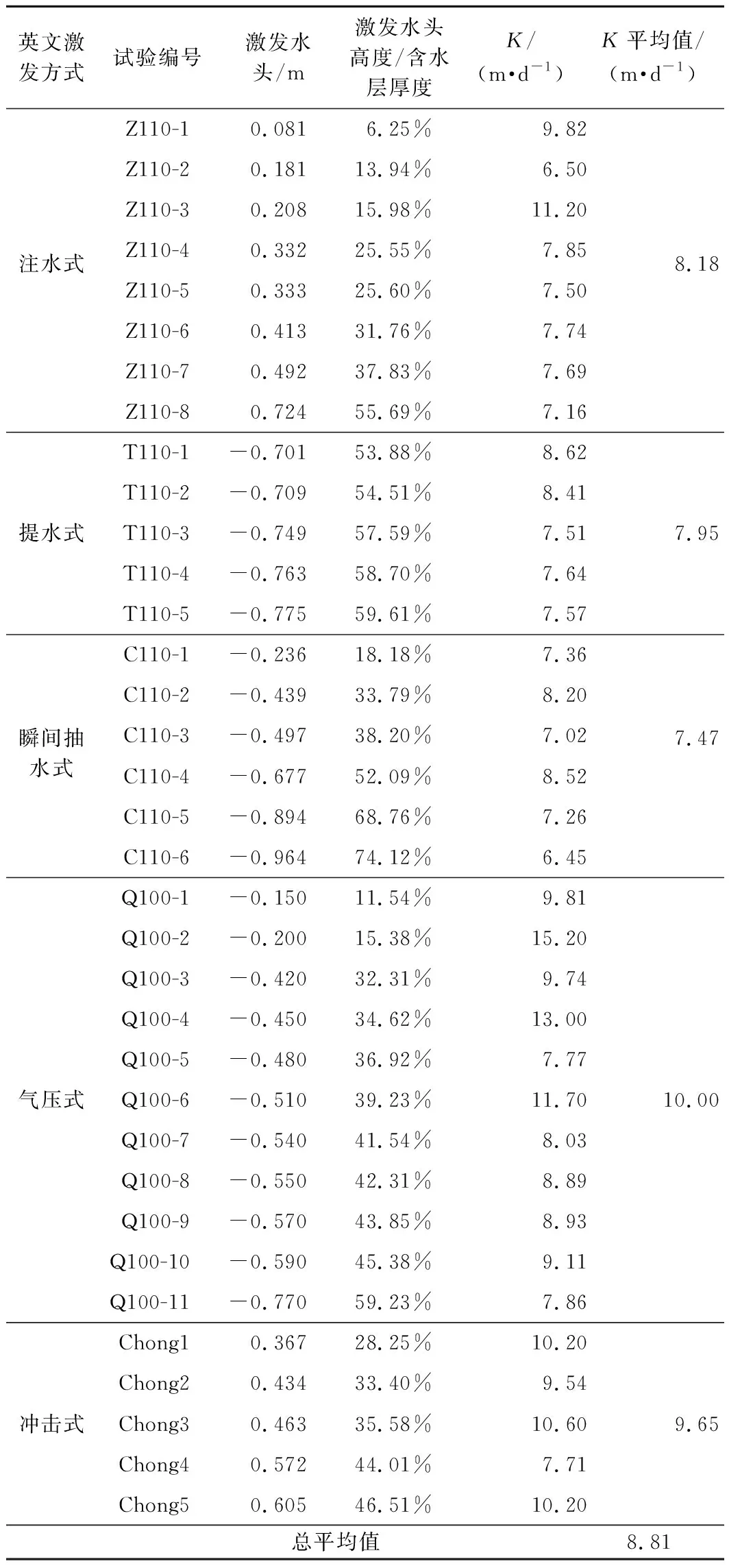
表1 110 mm孔径不同类型微水试验
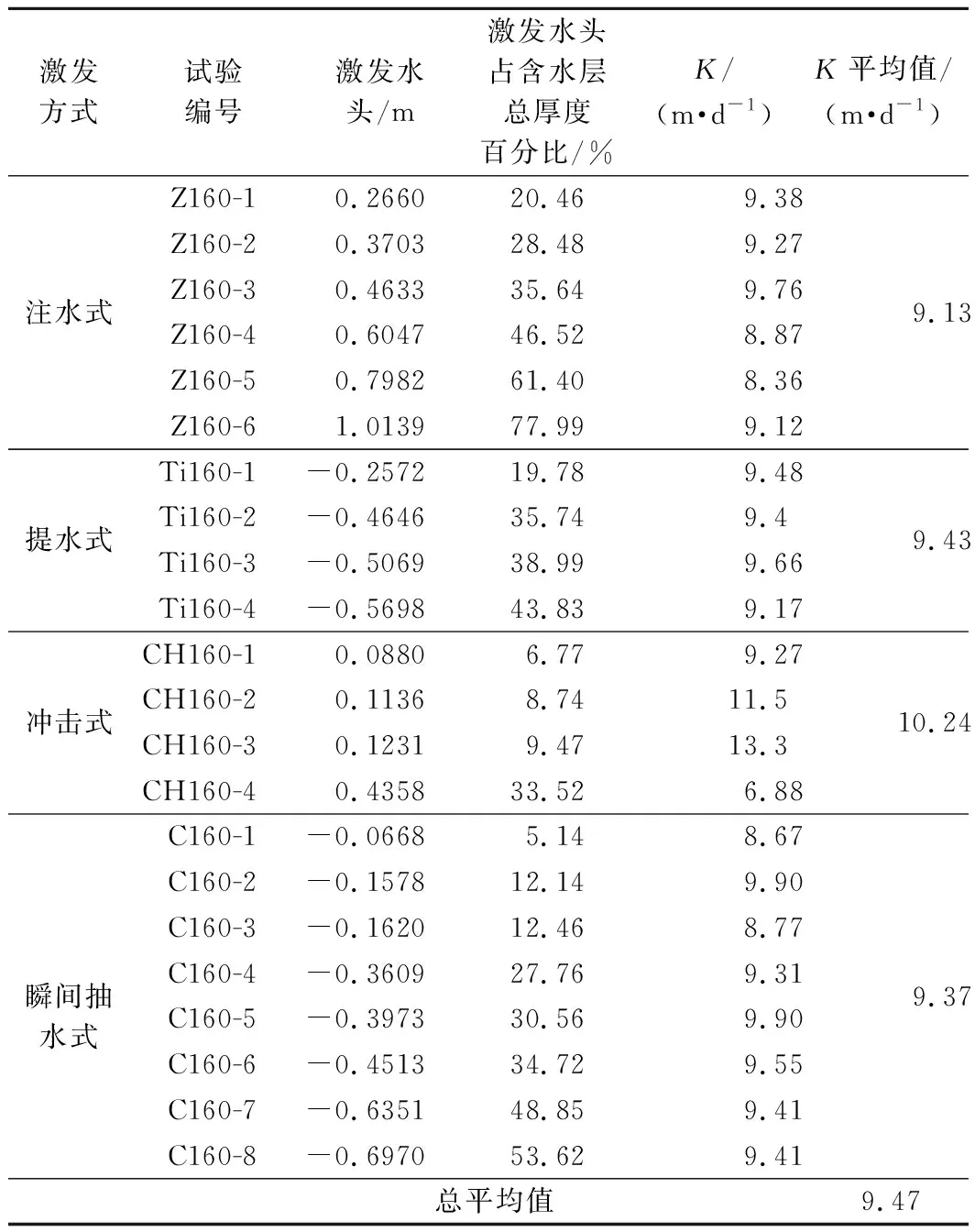
表2 160 mm孔径不同类型微水试验
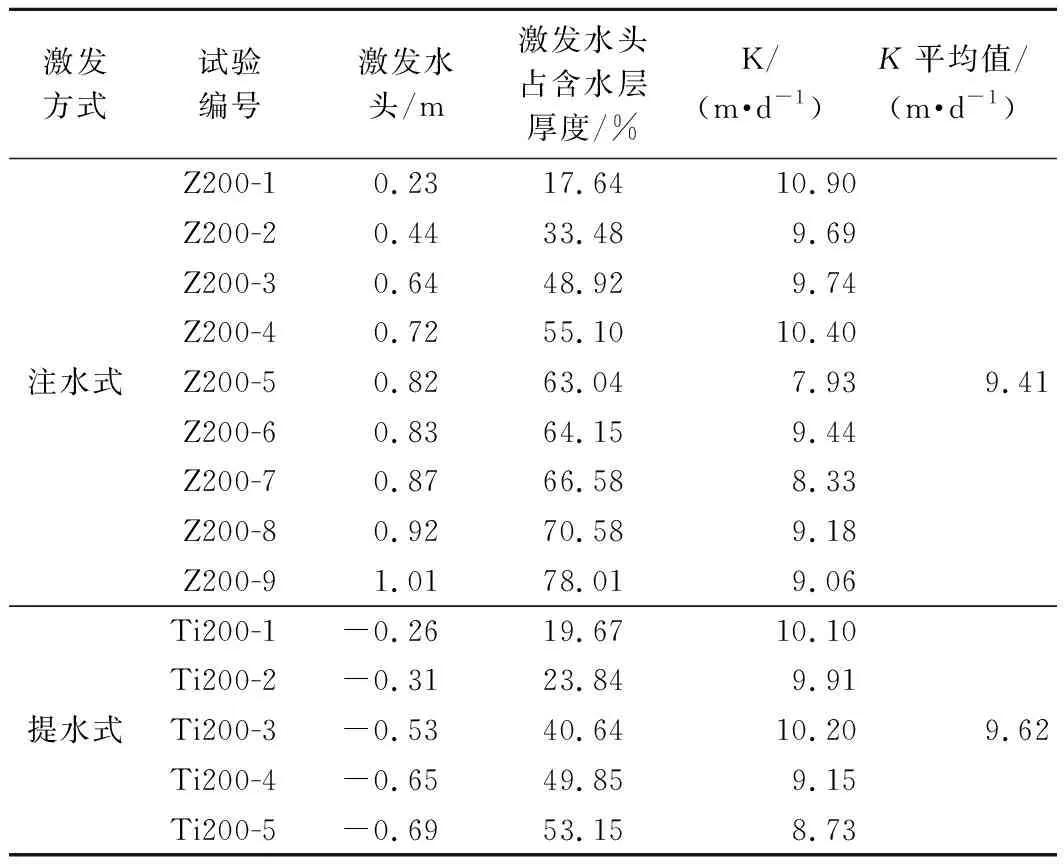
表3 200 mm孔径不同类型微水试验
从表1~3可以看出,不同孔径、不同激发方式计算出渗透系数K值的平均值为7.47~10.24 m/d。冲击式微水试验计算结果较其他方式略偏大,其主要原因是冲击式微水试验在重物坠入孔内地下水面时,造成的水面波动以及水花飞溅作用给试验带来了一定的影响,气压式微水试验仅在110 mm孔径中进行,由于加压过程干扰以及孔口密封性等原因,其结果离散性较大,其它类型的微水试验成果较为接近且相对稳定。不同孔径微水试验的成果也略有差异,其主要原因是在进行完一种孔径的微水试验后,需要将主孔周围的含水介质砂挖出,更换完主孔后再重新填实,重新填实后的砂层和原砂层的密实度存在差异,进而造成了试验结果的差异。
从表中还可以看出,同一激发方式下,计算出的K值较为接近,离散度较小,表明水头的激发强度对试验结果影响并不明显。但需要注意的是,激发强度越小,由于水位变化幅度小,对水位恢复过程中的水位观测精度、抗干扰等要求也较高,激发强度越大,计算结果相对稳定。
另外,对试验过程中观测孔的观测水位变化结果表明,激发强度越大,试验的影响范围也相对大,在本次试验中,在激发强度小于50%时,试验的影响范围约为0.7~1.0 m,大于50%时,影响范围扩展到大于1.0 m,最大激发强度达到70%以上时,影响范围已接近含水层的圆岛边界,根据圆岛边缘的G4观测孔观测数据,影响幅度0.05~0.15 cm。研究表明,激发强度越大,计算结果所能代表的试验孔周边含水层范围越大,对实际勘察工作越有利。这也给今后微水中激发强度的选择指明了方向,在现场具备快速水头变化条件的情况,应选择较大的激发强度。
4 结论
(1)本次利用多孔均质介质物理模型平台开展了不同形式不同水头激发高度(水头激发高度未超过含水层厚度)的微水试验,试验结果显示激发强度对试验结果有一定影响,但影响并不明显。
(2)在多孔均质含水层中,激发强度越大,微水试验的计算结果越稳定。激发强度越小,由于水位变化幅度小,对水位恢复过程中的水位观测精度、抗干扰等的要求也较高。
(3)激发强度越大,微水试验的影响范围也相对大,在现场具备快速水头变化条件的情况,应选择较大的激发强度。
