CAESARⅡ在烟风管道应力计算中的应用

汪佳杰

1 CAESARⅡ参数设置

利用CAESARⅡ进行烟风管道计算，参数的初始设置与汽水管道有所不同，除了管径及壁厚明显有别于汽水管道外，还有一些特殊设定。当我们输入管径及壁厚时，软件会自动分析计算管道管径与壁厚的比值，当比值>100时，软件默认此管道为大薄壁管道，相似模拟为我们所应用的锅炉烟风管道。

其他设置要点为：

（1）钢板卷制的焊接管道，选择有焊缝；填写焊接接头系数：WI=0.8；

（2）加工偏差：0.0；腐蚀余量：0.3；

（3）材质选择：选用许用应力和密度与设计中管道材质相同或相近的钢板；

（4）根据项目实际要求设定温度、压力、流体介质密度、内保温厚度及密度、外保温厚度及密度。由于烟风管道为负压，填写0即可；

（5）弯头转弯半径设置，选取：short短半径（R=D，即半径等于一倍直径，接近设计规范要求）；

（6）烟风阀门设置为：刚性件，并输入重量，作为局部荷载；

（7）膨胀节设置：输入轴向刚度、径向刚度、扭曲刚度（避免扭曲变形，因此默认无限大，输入1E10）、设备有效直径。具体如图1所示。

图1 经典管道输入

2 CAESARⅡ软件适用范围

适用于烟风管道弯头角度5°～95°范围内的管道结构体系。若管道弯头角度超出此范围，需适当简化模型，以适应软件的应用范围。将管道简化为梁单元进行设计计算，将管道中弯头简化为刚体进行设计计算。所有的实际管道，在计算前均应进行相应的模型简化以适应软件的应用范围。

3 人工理论与计算机CAESARⅡ软件两种烟风管道应力计算方案对比

现以某一管道实例进行计算，对比两种烟风管道应力计算方案。

3.1 管道参数

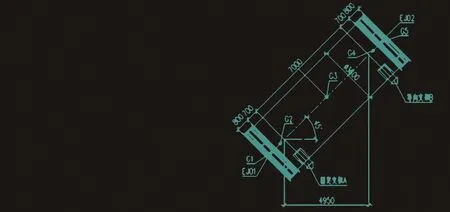
管道布置如图2，已知条件见表1。

图2 管道布置图

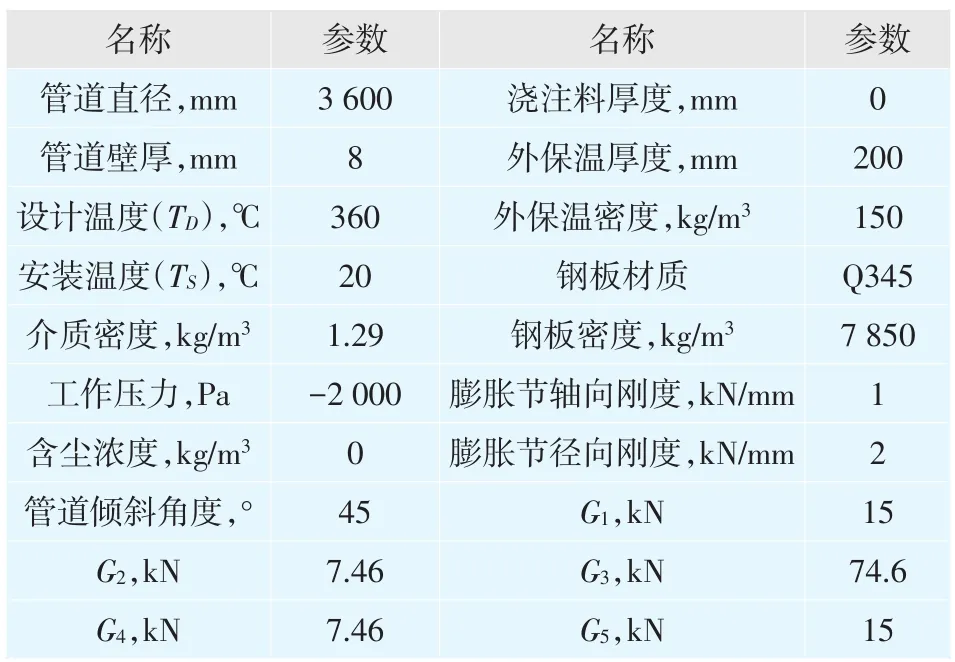
表1 已知条件

已知：膨胀节EJ01端点位移量：ΔX=0mm，ΔY=0mm，ΔZ=20mm Rx=0， Ry=0， Rz=0

可得出1号膨胀节轴向受力1：

f1轴1=×20×sin45°×1=7.07kN

管道受热后1号膨胀节轴向压缩量：

m=1 500×360×12.84×10-6=6.9mm

可得出1号膨胀节轴向反力2：

叠加得出：

f1轴=f1轴1+f1轴2

=7.07+3.45=10.52kN

1号膨胀节径向反力：

f1径=20×cos45°×2=28.28kN

按坐标进行受力分解：

f1轴x=7.44kN；f1轴z=7.44kN

f1径x=20kN；f1径z=20kN

已知膨胀节EJ02端点位移量：

ΔX=0mm，ΔY=0mm，ΔZ=-15mm

Rx=0， Ry=0， Rz=0

可得出2号膨胀节轴向反力1：

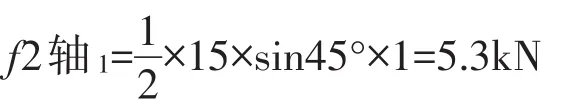
管道受热后2号膨胀节轴向压缩量：

m=8 500×360×12.84×10-6=39.3mm

可得出2号膨胀节轴向反力2：

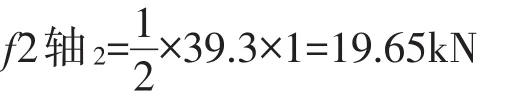
叠加得出：

f2轴=f2轴1+f2轴2=5.3+19.65=24.95kN

2号膨胀节径向反力：

f2径=15×cos45°×2=21.2kN

按坐标进行受力分解：

f2轴x=17.64kN；f2轴z=17.64kN

f2径x=15kN；f2径z=15kN

3.2 理论公式计算

（1）管道冷态受力分析简化模型见图3。力平衡：

∑Fx=0得:Fx+Fbx=0

①Fx=-Fbx=-Fbsin45°

∑Fz=0 得:Fz+Fbcos45°-G1-G2-G3-G4-G5=0

②Fz=119.52kN-Fbcos45°

弯矩平衡：

∑MA=0

MA+G3×L3+G4×L4+G5×L5

图3 管道冷态受力分析简化模型

=G1×L1+G2×L2+Fb×Lb

③MA=G1×L1+G2×L2+Fb×Lb-G3×L3

-G4×L4-G5×L5

=15×0.777+7.46×0.247+Fb×7-74.6×2.475

-7.46×5.197-15×5.727

=Fb×7-295.812

式中：

Fx、Fz——固定支架水平支撑力及竖直支撑力

Fb——导向支架支撑力

Fbx、Fbz——支撑力Fb在水平和垂直方向的分力

Lb——导向支架到固定点A的垂直距离，即力臂

MA——简支梁在固定点A的弯矩

G1～G5——管道及膨胀节的荷载

L1～L5——G1～G5到固定点A的垂直距离，即力臂

挠度平衡（超静定结构力系，列挠曲轴方程，见图4）：

首先根据挠曲轴方程的要求，进行坐标系转化，使导向支架受力方向垂直于新坐标系X＇轴，转化后坐标系如图5所示（为了便于观察，将管系顺时针旋转45°）。

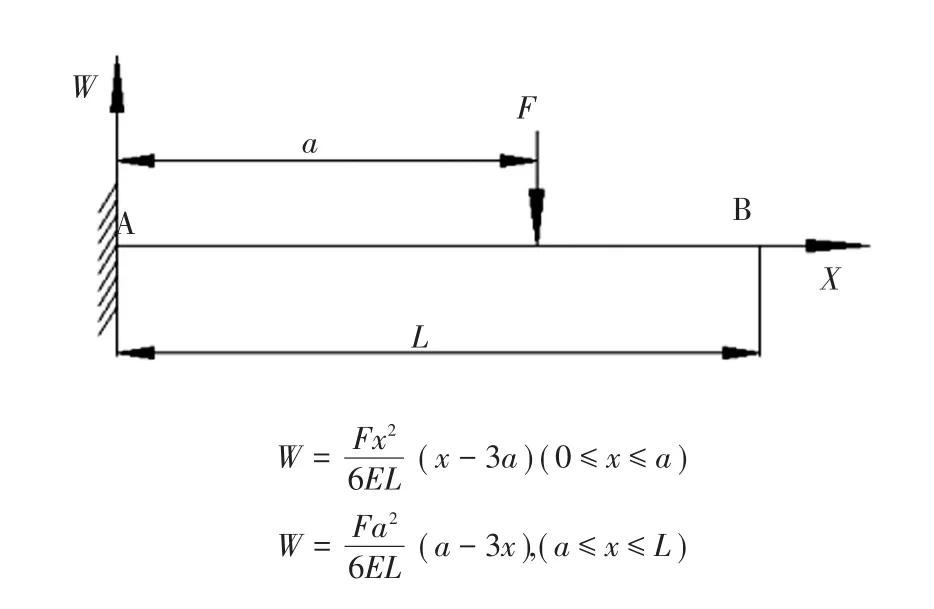
图4 挠度平衡（超静定结构力系，列挠曲轴方程）

图5 转化后坐标系图

列解方程x＇=B点，重力作用下的挠度与导向支架作用下的挠度相等：

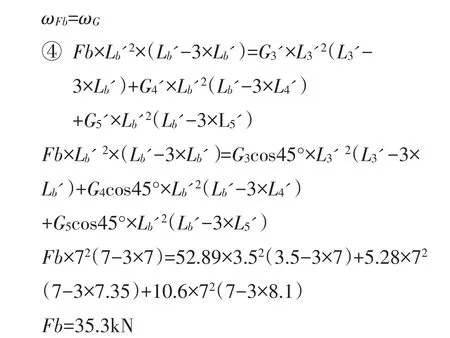
式中：

ωFb——导向支架支撑力Fb作用下B点的挠度

ωG——各个重力作用下B点的挠度

Fb——导向支架支撑力

Lb＇——导向支架支撑力Fb到固定点的距离

G3＇～G5＇——管道重力在X＇轴的分力

L3＇～L5＇——各个重力点到固定点的距离

将此结果代入①、②、③式中，可得出冷态工况下支座反力:

（2）管道热态受力分析简化模型见图6。

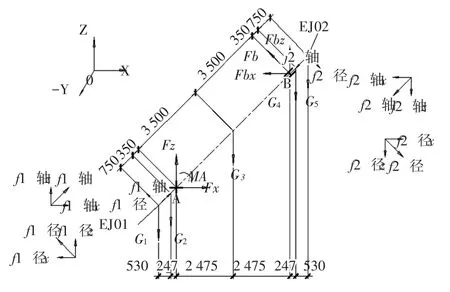
图6 管道热态受力分析简化模型

力平衡：

∑Fx=0

得：Fx+f1轴x+f2径x-Fbx-f1径x-f2轴x=0

① Fx=Fbsin45°+20+17.64-7.44-15

∑Fz=0

得:Fz+Fbcos45°+f1轴z+f1径z-G1-G2-G3-G4-G5-f2轴z-f2径z=0

②Fz=124.72kN-Fbcos45°

弯矩平衡：∑MA=0

MA+G3×L3+G4×L4+G5×L5+f2径×Lf2+f1径×Lf1=G1×L1+G2×L2+Fb×Lb

③ MA=G1×L1+G2×L2+Fb×Lb-G3×L3-G4×L4-G5×L5-f2径×Lf2-f1径×Lf1

MA=Fb×7-496.9

式中：

Fx、Fz——固定支架水平支撑力及竖直支撑力

Fb——导向支架支撑力

Fbx、Fbz——支撑力Fb在水平和垂直方向的分力

Lb——导向支架到固定点A的垂直距离，即力臂

MA——简支梁在固定点A的弯矩

G1～G5——管道及膨胀节的荷载

L1～L5——G1～G5到固定点A的垂直距离，即力臂

f1轴x、f1轴z——1号膨胀节轴向热态反力f1轴在x及z轴的分力

f2轴x、f2轴z——2号膨胀节轴向热态反力f2轴在x及z轴的分力

f1径x、f1径z——1号膨胀节径向热态反力f1径在x及z轴的分力

f2径x、f2径z——2号膨胀节径向热态反力f2径在x及z轴的分力

Lf1、Lf2——1号膨胀节径向力f1径及2号膨胀节径向力f2径到固定点的力臂

挠度平衡（超静定结构力系，列挠曲轴方程，见图4）：

首先根据挠曲轴方程的要求，进行坐标系转化，使导向支架受力方向垂直于坐标系X＇轴，转化后坐标系如图7所示（为了便于观看，将管系顺时针旋转45°）。

列解方程x＇=B点，重力、膨胀节径向力作用下的挠度与导向支架作用下的挠度相等：

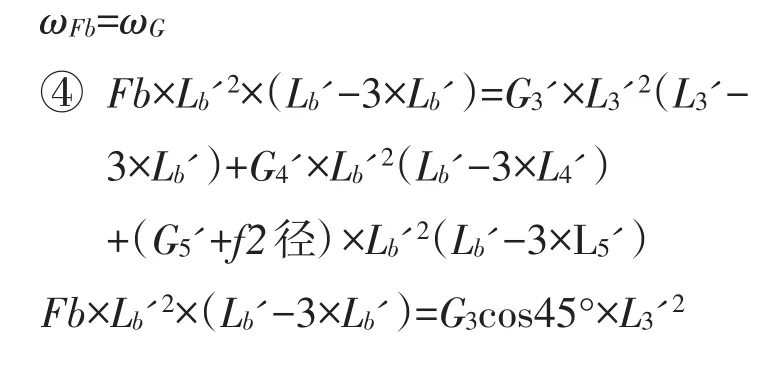
图7 转化后坐标系图

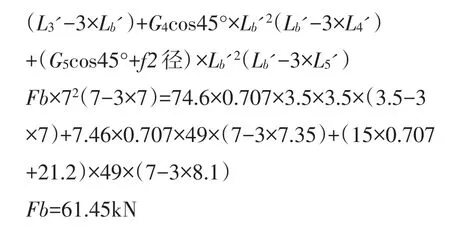
式中：

ωFb——导向支架支撑力Fb作用下B点的挠度

ωG——各个重力作用下B点的挠度

Fb——导向支架支撑力

Lb＇——导向支架支撑力Fb到固定点的距离

f2径——膨胀节径向热态反力

G3＇～G5＇——管道重力在X＇轴的分力

L3＇～L5＇——各个重力点到固定点的距离

将此结果代入①、②、③式中，可得出热态工况下支座反力:

3.3 利用CAESARⅡ软件建模计算

3.3.1 输入已知初始条件，建立管道模型

（1）由于管道为负压管道，介质压力的作用对管道受力影响很小，且管道只计算正压力，因此介质压力设置为0。

（2）设置膨胀节时，除了上面提到的一些参数外，还要设置膨胀节的重量，采用在膨胀节两端加入刚性件的方法，输入刚性件重量，作为局部荷载。若不做设置则软件默认膨胀节重量为0，影响受力计算。

（3）设置起止点的端点热位移，该设置是模拟设备端点位移，例如锅炉进出口热位移等，可视作固定点。由于设备端口受热后发生位移，从而挤压膨胀节变形，产生轴径向推力，这些力与管道热胀后的膨胀力联合作用于支架，使支架的受力情况更加复杂。

此次计算将垂直位移分解到管道的轴向和径向方向，以计算膨胀节的实际压缩量。

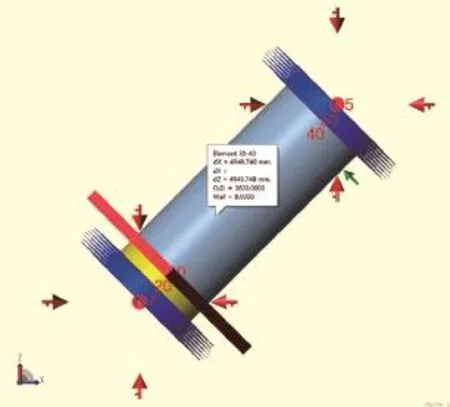
图8 管道模型

在此实例计算中，没有考虑导向支架摩擦力，因为软件的计算方法为基本有限元的方法，利用结果收敛，反复迭代，当加入摩擦力后整个管系模型的刚度发生变化，导致支架所受的正压力变化，摩擦力亦随之变化。反复迭代的过程是人工计算无法实现的，所以此次计算未考虑摩擦力，即默认滑动摩擦系数为0。具体参数设置如图8～15所示。

3.3.2 运行软件进行计算

输出计算结果的支座反力：CASE 1（热态工况）：（OPE）W+D1+T1+P1；CASE 3（冷态工况）：（SUS）W+P1；节点30：固定支座；节点 40：导向支座；节点10：起点；节点60：终点。输出计算结果见表2。

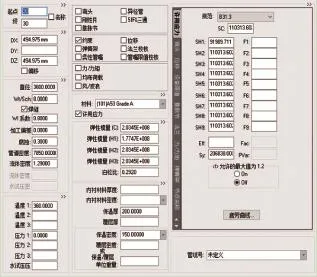
图9 基本参数设置

图10 膨胀节参数设置

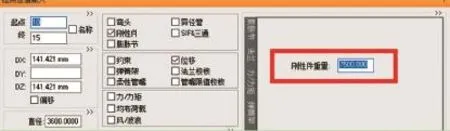
图11 膨胀节重量设置

图12 固定支架设置

图13 导向支架设置

图14 终点热位移设置

图15 起点热位移设置

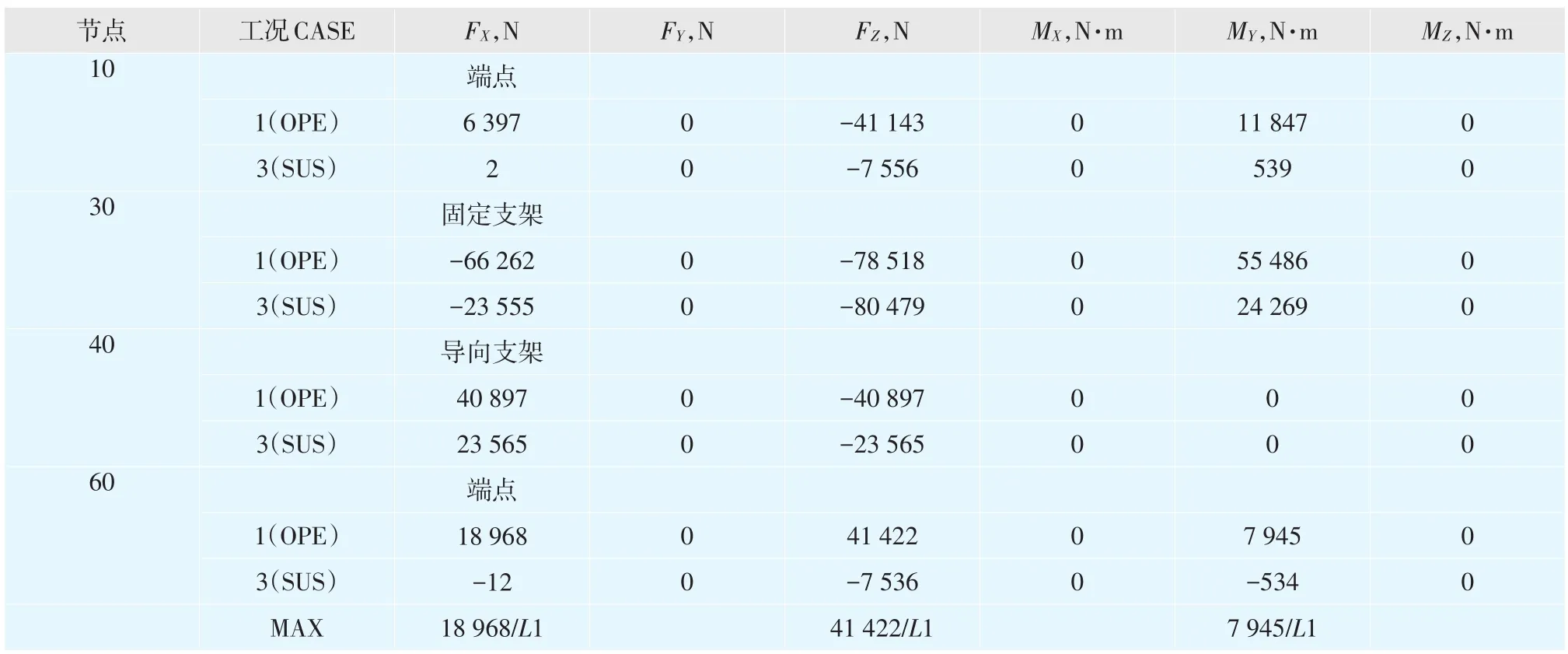
表2 输出计算结果

3.4 计算结果对比分析

通过上述两种计算方法的结果对比可以看出，对于固定支座从冷态到热态，随着温度的升高，支架的水平力逐渐增加，垂直力逐渐下降。从冷态到热态弯矩方向不变，但是温度升高后，受膨胀节径向膨胀力的影响，弯矩会沿顺时针方向越来越大。对于导向支架，当温度升高后，2号膨胀节产生径向变形，形成径向膨胀力，在其作用下管道发生挠度变形，管道方向与导向支架的方向相反，这就意味着导向支座在管道受热后要提供更大的力来补偿径向膨胀力造成的管道变形。导向支架受力增加也正是导致固定支架在热态工况竖直受力减少的原因。

不难看出，虽然两种计算方法得到的支座受力的数值相差不大，各个受力方向相同，冷热态受力变化趋势也相同，但还是有一定的差异性。实际在模型简化计算过程中是存在一定差异的，人工计算是将膨胀节与设备断开进行的，作为一个理想的孤立的受力体系建立模型。热态中将膨胀力人工计算后加入受力分析体系再列解平衡方程、挠度方程进行求解。实际运行过程中是不存在这种孤立的体系的，它必然是要和设备连接到一起，与设备端口去分担这部分荷载。软件的计算过程会将管道端点设定热位移数值，与设备端点联合起来作为一个整体力系考虑，计算出端点推力及弯矩，这样也可以核算出端点的安全性与稳定性。在人工计算中会人为地选取设备的重心、量取力矩等，这些都会与软件存在一定的差异性，因此造成计算结果的差异。

CAESARⅡ软件的计算是建立在更加贴近工程实际的前提下，只要模型输入的初始参数没有问题，计算结果可以更加有保证，与人工计算相比，模型计算的优势更加明显。我们可以通过调整支架形式、支架位置、膨胀节位置等来比较哪种设置更加合理，支架水平力及弯矩最小，在可实现的合理的范围内找到一个更加经济可行的实施方案，最大程度地降低土建支架钢结构成本，达到设计优化的最终目的。

4 结语

烟风管道受力复杂，工况较多，难于进行精准计算，通过调整CAESARⅡ软件的相关设置，提高了高温烟风管道计算的精准性。利用CAESARⅡ进行烟风管道计算，可大大减少手动计算量，降低了计算出错的概率，从而有效避免了工程事故的发生。CAESARⅡ的工况模拟更加贴近实际生产运行工况，管道简化为梁单元计算也是目前被认可的计算方法，有限元分析理论也具备可靠性与准确性。多年来,烟风管道频频出现各种各样的问题，因此确保支架合理，受力计算安全、可靠显得尤为重要。利用CAESARⅡ软件还可以出具格式规整的应力计算书，包括节点位移、节点应力、端点推力、支座反力等信息，更具说服力。因此，利用CAESARⅡ软件进行烟风管道支架受力计算具备可行性与高效性，可广泛应用于今后的工程设计中。