简支梁正交异性钢桥面铺装层最不利受力分析
2018-12-13宋君超周艳孟灵玥李想
宋君超周艳孟灵玥李想
(1.济南黄河路桥建设集团有限公司,山东济南250014;2.山东建筑大学道路与交通工程山东省高校重点实验室,山东 济南250101;3.山东外事翻译职业学院国际商学院,山东 威海264506;4.大华会计师事务所(特殊普通合伙),北京100039)
0 引言
正交异性钢桥面板作为大跨度钢箱梁桥的桥面板在大跨度钢桥建设中的应用越来越广泛,但同时正交异性钢桥面铺装的早期损坏问题却一直没有得到很好的解决。桥面铺装的好坏直接影响桥梁使用的舒适、经济和安全,频繁的维修必然耗费大量的人力、物力并影响通行能力[1-2]。因此,研究钢箱梁桥面板铺装层在荷载作用下产生的最大应力、应变,用以修正当前正交异性钢桥面铺装结构设计指标是非常重要的。如果铺装材料能够满足最不利荷载作用下钢桥面铺装层内产生的应力和应变,那么铺装结构就能够避免早期损坏,提高使用寿命,并产生巨大的经济和社会效益。
我国目前对各种桥型的正交异性钢桥面铺装在车辆荷载作用下的响应均有研究,正交异性钢桥面铺装的受力分析数值模拟方法有整体模型法、多尺度模型法(混合单元法)、子模型法、简化模型法等。在研究中模型大部分采用简化模型[3-11],未考虑桥型的影响,也并未考虑荷载作用位置对简支梁桥面铺装受力的影响[12-13]。在实际荷载作用下,正交异性钢桥面铺装内最大应力、应变的位置和大小,对钢桥面铺装材料和结构的设计至关重要。整体模型为带有桥面铺装结构的桥梁整体板壳模型,这种有限元分析方法是最精确的。然而,该模型建模复杂,且实际应用中会受到计算机内存的限制,因此桥面铺装分析中很少采用此方法[14-15]。文章建立了最接近简支梁钢桥面铺装真实受力特性的整体模型,施加移动荷载,确定在桥面铺装中最大纵向压应力的荷载作用位置,并分析桥面铺装的受力特性。
1 简支梁桥整体模型的建立
简支梁桥跨径为48 m、桥宽为22 m,两侧翼板宽为3 m,单箱四室,每隔3 m有1道横隔板,中间横隔板开人孔,端横隔板为实心截面,简支梁横截面具体尺寸如图1(a)所示。其中,横桥向为x轴,截面右侧为正、左侧为负;竖桥向为y轴,截面上侧为正、下侧为负;纵桥向为z轴。Sx、Sy、Sz分别为x、y、z向应力,SEQV为等效应力。

图1 简支梁整体模型横断面及荷载布置图
利用ANSYS建立简支梁桥的整体模型,钢箱梁采用 SHELL63单元,桥面铺装沥青混凝土采用SOLID45单元,荷载采用SURF154单元施加。钢材及沥青混凝土材料均为弹性材料,各向同性,钢材弹性模量2.1×108MPa、密度为 7850 kg/m3、泊松比为0.3。桥面铺装材料为沥青混凝土,弹性模量取常用值1000 MPa、密度为 2400 kg/m3、泊松比为 0.2,沥青混凝土铺装厚度为50 mm,桥面铺装层划分为一层,桥面铺装与桥面板之间采用共用节点完全连接,位移连续。整体模型梁端部腹板位置底板处通过厚20 cm钢板支座施加简支梁边界条件,边界条件施加见表1。

表1 简支梁边界条件表
荷载作用采用双向四车道车辆荷载,纵向荷载作用位置根据移动荷载下使跨中产生最大应力的荷载作用位置确定。车辆荷载标准如图1(b)所示。荷载横向沿中心线两侧对称布置,车辆从简支梁一端以80 km/h的速度驶入,行驶到另一端共加载306步。四车道荷载在横桥向相对于梁中轴线对称布置,为方便计算,布置为同向荷载。一侧两车道4个轮载中心作用位置分别距中心线2.15、3.95、5.25和7.05 m,荷载作用面积为0.6 m×0.2 m。
2 简支梁正交异性钢桥面铺装层最不利受力分析
2.1 移动荷载下正交异性钢桥面铺装层整体受力分析
移动荷载作用306步后,将梁横向-6.75 m处纵向正交异性钢桥面铺装顶面各点在荷载从梁一端行驶到另一端时产生的纵向应力(Sz)最大和最小值绘制成曲线,如图2所示。可以看出,横隔板位置处桥面铺装顶面的应力较小,在两横隔板之间位置,应力较大,在梁近跨中22.6 m处产生的应力最大。梁截面上其它荷载作用位置处桥面铺装顶面纵向各点所得纵向应力有相似规律。
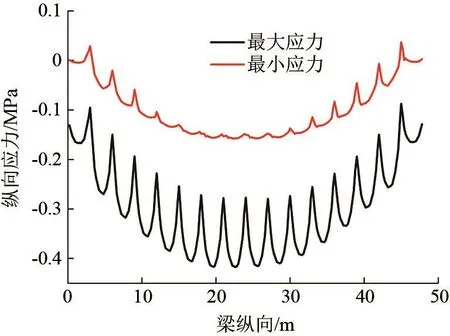
图2 梁横向-6.75 m处纵向各点在306步时间中产生的纵向最大和最小应力包络图
梁纵向22.6 m和横向-3.65 m处桥面铺装顶面点的应力—时间曲线如图3所示。可以看出,当车辆荷载第2根到第4根轴,轴重分别为 120和140 kN的轴经过22.6 m点时,引起该点的各向应力均较大。当第4根轴经过该点时,产生的应力值最大,此时,车辆荷载最后轴作用于纵向21.4 m处。
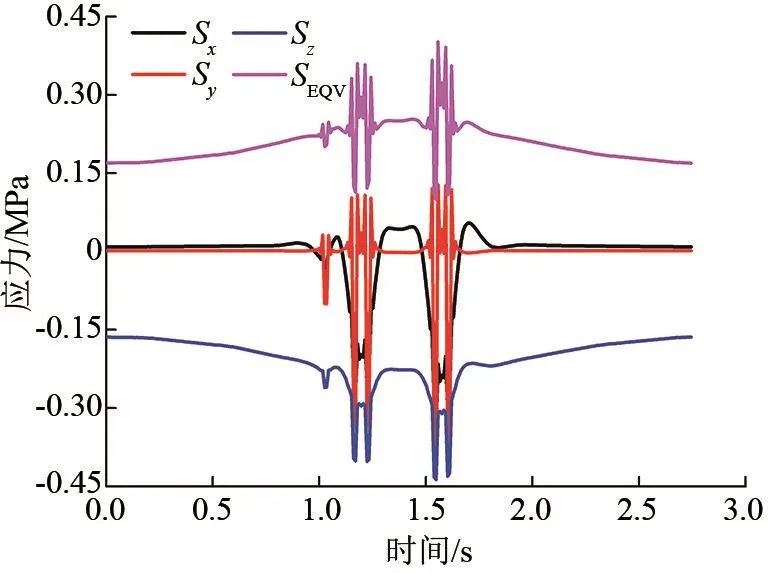
图3 梁纵向22.6 m和横向-3.65 m处应力—时间曲线图
梁横向-6.75 m荷位处纵向各点的纵向应力—时间曲线如图4所示,可以看出,车轮作用处各点的应力—时间历程曲线有相似规律,车轴经过该点时应力较大,因此有2个峰值。2个120 kN的轴经过时形成1个峰值,2个140 kN的轴经过时形成1个峰值,越接近跨中,应力越大。而横隔板处形成的峰值与2横隔板之间的点形成峰值的方向相反,因横隔板有竖向支撑作用,故形成反峰。梁纵向22.6 m和横向-4 m腹板位置的应力—时间曲线如图5所示,在腹板位置,x向应力比较大,同样在荷载经过时形成2个峰值。腹板处铺装层顶面纵向各点应力具有相似的规律。
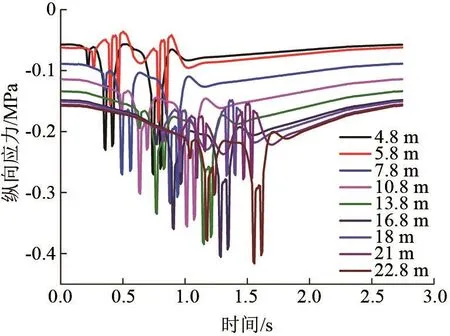
图4 梁横向-6.75 m纵向各点应力—时间历程曲线图
梁纵向27 m和横隔板位置横向-4 m腹板及-3.65 m荷位处应力—时间历程曲线如图6所示,可见横隔板处车辆未经过该点时,应力很小,车轴经过时形成的应力峰值也较小,在横隔板和腹板交界点处各向应力均较小,而横隔板上腹板之间的位置,竖向应力较大。各点应变—时间历程曲线与应力—时间历程曲线相似。
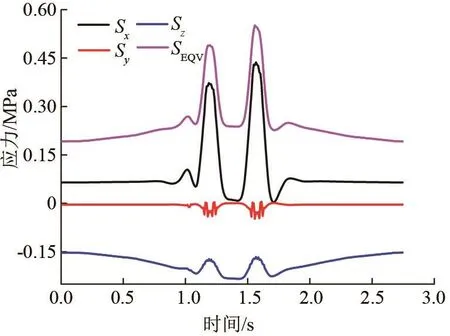
图5 梁纵向22.6 m横向-4 m位置桥面铺装顶面处应力—时间历程曲线图
当车辆行驶到173步,后轴作用于21.4 m时,在梁纵向22.6 m的位置梁横截面上各点的应力应变值如图 7 所示。Ex、Ey、Ez分别为x、y、z向应变,EEQV为等效应变。横截面上轮载作用中心桥面铺装顶面位置的各向应力、应变较大,横截面-4 m、4 m腹板位置上,横向(x向)拉应力、拉应变较大,等效应变最大值为5.63×10-4。
当车辆行驶到173步,后轴作用于21.4 m时,梁横向荷载作用位置-3.65 m处纵向各点应力如图8(a)所示,车轴通过的位置纵向应力和竖向应力最大,竖向应力有正负交变。
当车辆行驶到173步,后轴作用于21.4 m时,梁横向-4 m处腹板位置桥面铺装顶面纵向各点应力如图8(b)所示,车轴通过位置的水平向应力最大,具有较大的水平拉应力和拉应变。
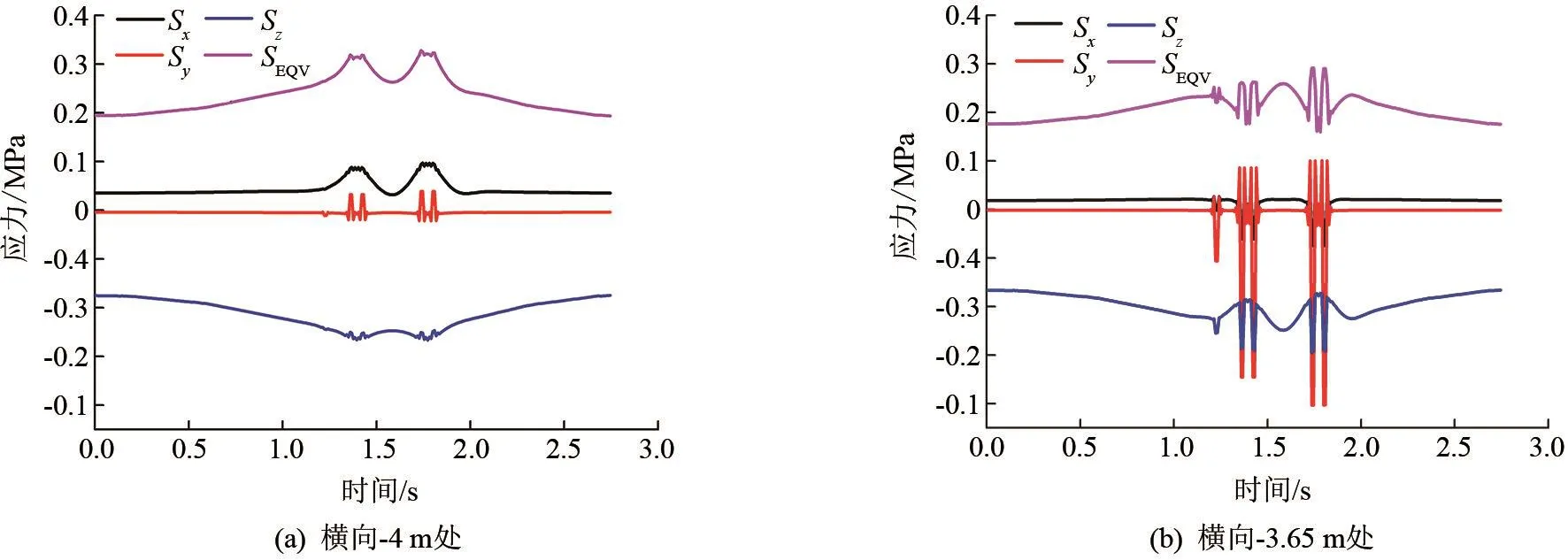
图6 梁纵向27 m桥面铺装顶面点应力—时间历程曲线图
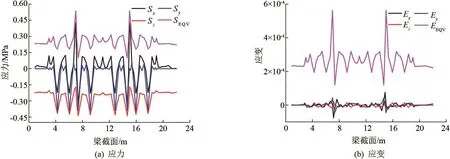
图7 第173步22.6 m处梁横截面上各点应力和应变图
2.2 正交异性钢桥面铺装层最大应力应变分析
通过移动荷载下简支梁桥的整体受力分析,确定荷载最不利作用位置,将模型细化,模型为正交异性钢桥面板钢箱梁桥,钢材采用16 Mn。加密荷载作用部分,加密部分单元尺寸为0.1,满足单元精度要求。模型其他条件与初步分析模型相同,将桥面铺装层分为5层,重新进行计算。模型细部尺寸及钢板厚度见表2,整体模型如图9所示。

图8 第173步横向-3.65 m和-4 m处梁纵向各点应力图
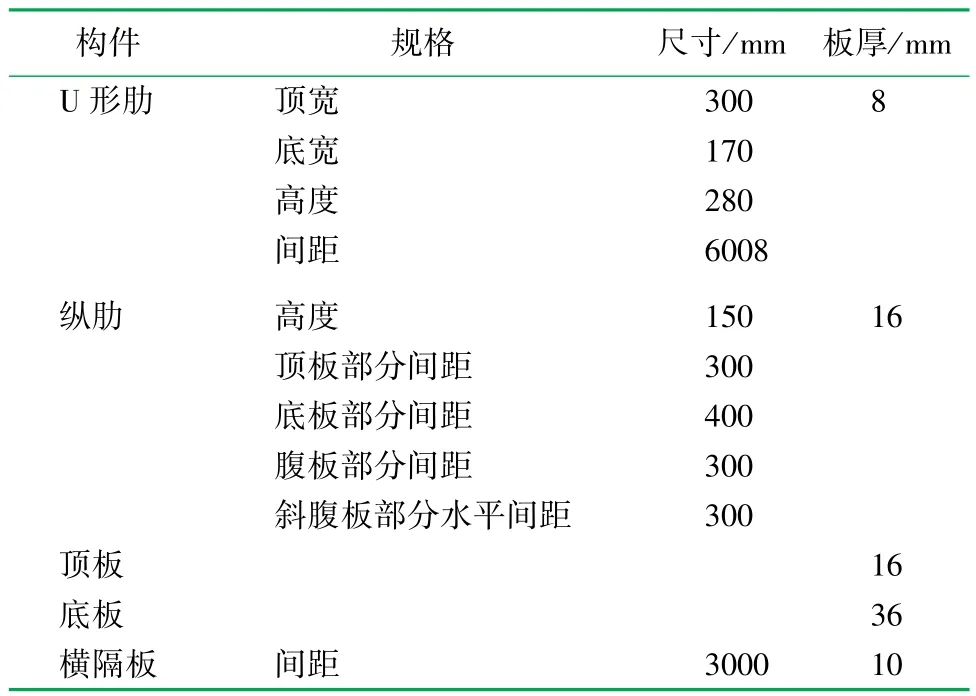
表2 简支梁整体模型表
通过对简支梁整体模型分析,得到桥面铺装层内各向应力应变最大值,结果见表3;铺装层各层各方向的最大最小应力应变值及产生位置见表4。铺装层各层次的横向最大拉应力由顶层向下逐渐减小,其中最大的拉应力发生在腹板处桥面铺装最顶面。竖向压应力和拉应力由顶面至底面依次增大,最大压应力发生在横桥向荷位中心6.75 m处铺装层底面;而竖向最大拉应变发生在横桥向3.5 m处,且从顶面到底面依次减小。纵向压应力、压应变均从顶面向下依次减小,最大值发生在横桥向3.8 m处;纵向拉应力、拉应变发生在纵桥向桥两端横向8 m处,且铺装层各层最大值均从顶面到下逐渐减小。

图9 简支梁整体有限元模型图
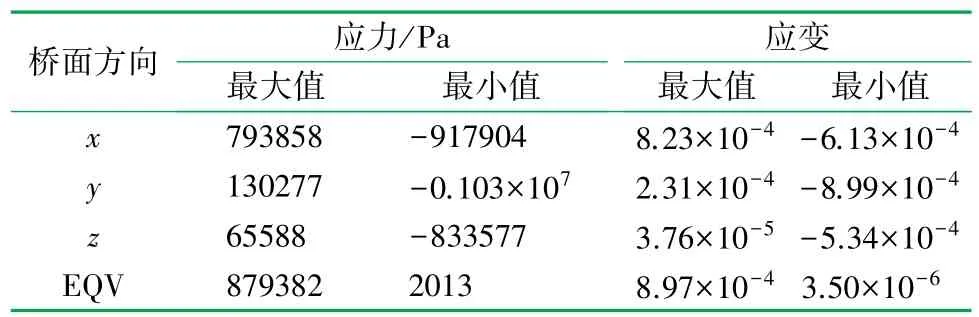
表3 简支梁桥整体模型桥面铺装层最大、最小应力表
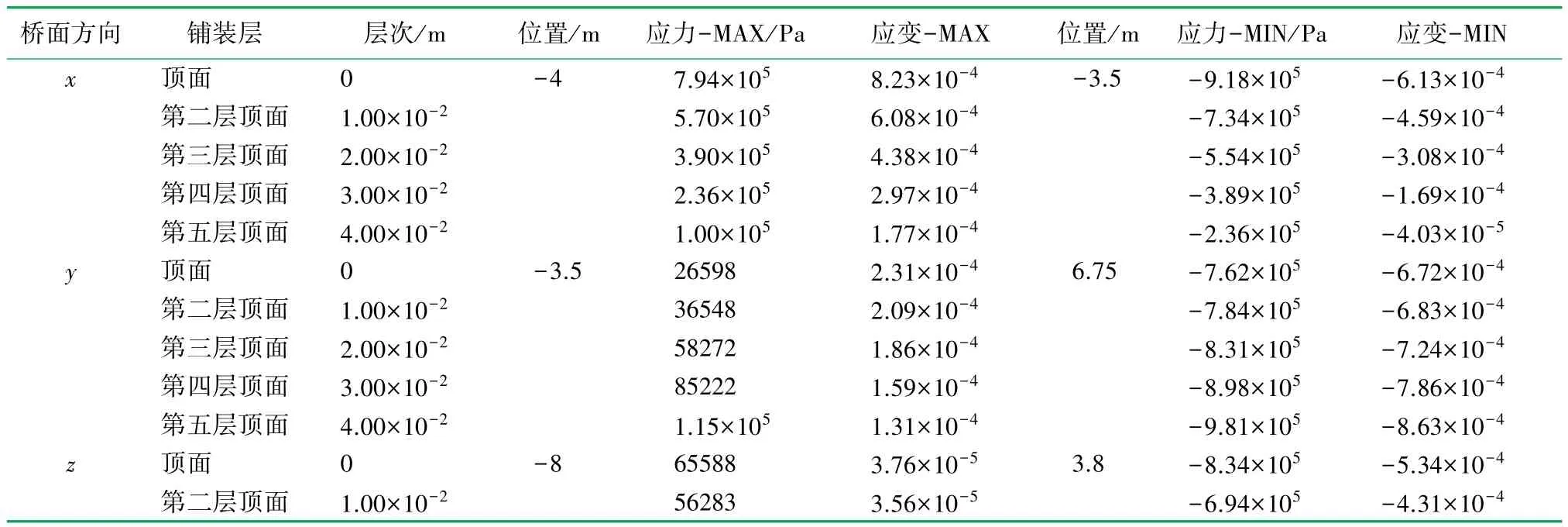
表4 简支梁桥桥面铺装各层次各方向最大及最小的应力、应变表
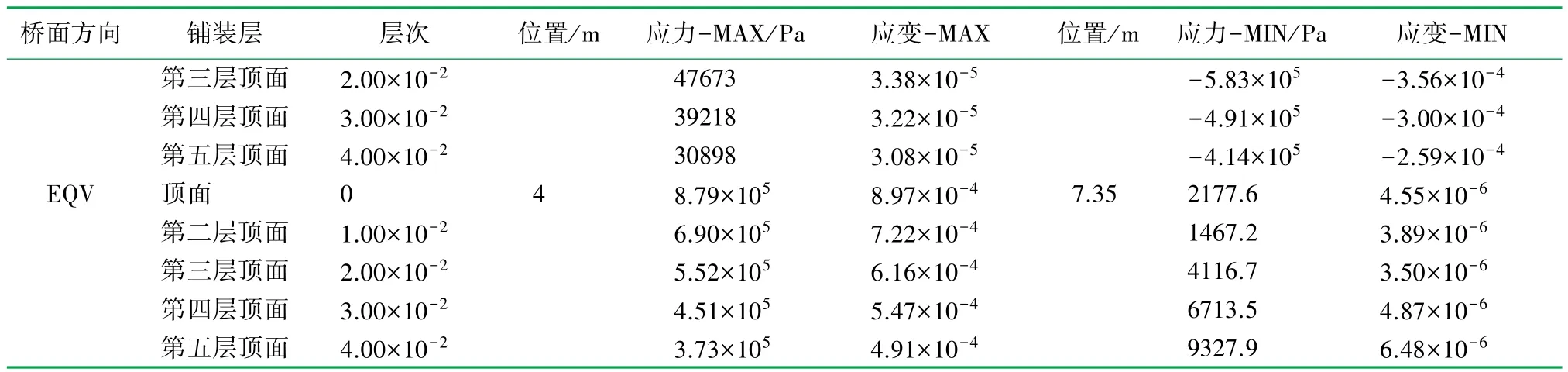
续表4
3 结论
通过在48 m跨径简支梁整体模型上施加移动荷载,计算桥面铺装层内各向应力应变的最大值位置,分析其最不利受力情况,得出以下结论:
(1)在移动荷载作用下,当车辆荷载后轴行驶至近跨中21.4 m时,跨径简支梁正交异性钢桥面铺装在纵向22.6 m处的应力最大。
(2)钢桥面铺装内,横向各层拉应力从顶面向下依次减小,其中最大拉应力发生在跨中附近腹板处桥面铺装最顶面;竖向最大拉应力从顶面到下依次增大,最大拉应变发生在横桥向3.5 m处,由顶面到下依次减小;纵向最大压应力、压应变发生在横桥向3.8 m处,从顶面向下依次减小。
