聚焦数学素养构建生本课堂

2018-12-13

新教育时代电子杂志(教师版) 2018年41期

（安徽省天长市城南小学安徽天长 239300）

数学素养是数学学科所固有的内蕴特性，是人通过后天学习所获得的数学知识技能、数学思想方法、数学能力、数学观念和数学品质融于身心的一种稳定的心理状态。作为一名数学教师，不能满足于教给学生知识，更应致力于全面提高学生的数学素养。笔者从“数感”、“几何直观”、“运算能力”、“推理能力”、“创新意识”等五个方面结合自己的教学实践，简要阐述如何培养小学生的数学素养，构建高效的生本课堂。[1]

一、经历数感活动，交流数感体验

美国瑞斯尼克教授这样说，“数感”是一种直觉，具有非算法性、复杂性（不可解释性）、不确定性等。简言之，数感是学生对数的感悟，它既是一种感知过程，也是一种思维过程，学生的思维具有个性化的特征，每个学生对数的感悟存在着差异，通过让学生交流自己的想法，不仅让他们体验到合作学习的快乐，更让他们在交流的过程中思维得到了碰撞，逐步形成对“数感”的孕育。

例如：苏教版四年级下册的“加法结合律”教学时，首先教师出示主题图，学生说出图中信息：跳绳的男生有28人，跳绳的女生有17人，还有23个女生踢毽子。学生根据信息提出“参加活动的一共有多少人？”这个问题并分析数量关系，尝试列出算式：28+17+23。在尝试计算时，多数孩子们通过观察，先计算17+23，再计算40+28，轻而易举地寻求出结果，然而有少数学生则按部就班的先算出28+17，再计算45+23，诚然，计算结果相同，但计算速度明显稍逊一筹，对数的感悟不强。在交流环节，数感较弱的学生汲取其他同学的观点和想法，采取了加法结合律，并通过举例验证使得自己的数感得以提升。[2]

二、依托数形维系，寻觅几何直观

“数缺形时少直观，形少数时难入微”。数形结合思想的天梯，帮助学生架设了一条通往数学天堂的快速便道。学生利用图形描述和分析问题，把复杂的数学问题变得简明、形象，充分展现了几何直观重要作用。

如探究“长方形的面积计算公式”的活动过程。

活动：用12个面积是1平方厘米的小正方形拼成一个长方形，你能拼出几种情况？

学生动手拼一拼：

师将学生的拼图情况列在表格里，方便观察。

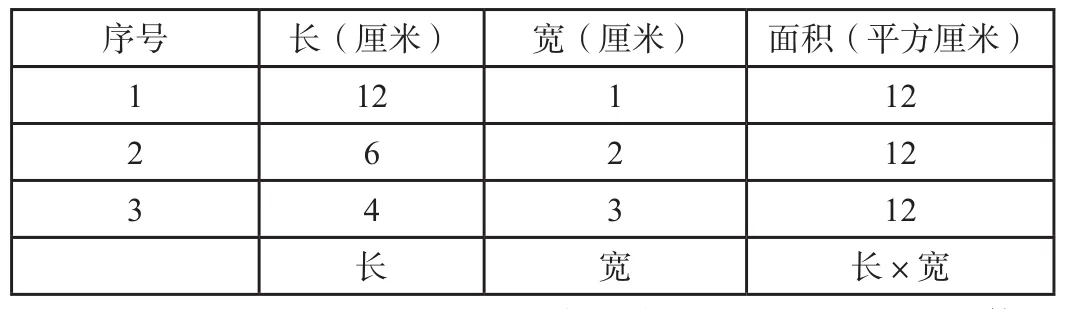
序号长（厘米）宽（厘米）面积（平方厘米）1 12 1 12 2 6 2 12 3 12长宽长×宽4 3

显然，此环节的探究活动是非常有效的，学生是学习的主体，教师是学生学习的组织者、引导者、合作者。学生借助数形结合的思想，展现了较强的几何直观的能力，通过举例归纳或者动手“移一移”、“拼一拼”、“算一算”等活动，自主完成了图形的面积计算公式构建过程。

三、借助操作实践活动，提升运算能力

皮亚杰认为：“活动是认识的基础，智慧从动作开始。”动手操作是发展数学思维、培养学生数学语言表达能力的重要方式之一，学生将自己的思维过程通过动手操作的过程展示出来，同时学生通过直观形象的操作，按步骤、有条理地表达自己思考的过程，使得动手操作、动脑思考和动口表达有机结合，促进感知有效地转化为内部的智力活动，促进学生对知识的理解。

如在教学“两位数加整十数”时，（课件呈现：大巴车有45个座位，小客车有30个座位，小轿车有3个座位，问：大巴车和小客车一共有多少个座位？）

列式：45+30=

笔者通过让学生摆小棒或者在计数器上拨珠子来理解算理，学生独立操作后汇报：

生1：先拿4捆小棒和5根小棒，把45分成40和5，再拿3捆；4捆加3捆是7捆，7捆是70根，70加5是75根，所以45+30=75。

生2：先在计数器十位上拨4颗珠子，个位上拨5颗珠子，即45，加上30，所以要在十位上再拨3颗珠子，结果就是十位上有7颗珠子，个位上有5颗，表示“75”。

师：你们这两种操作过程，有什么相同点？

生：都是先算40+30=70，再算70+5=75。

通过操作，学生的思维由抽象、模糊变得直观、清晰，能根据操作的过程将“两位数加整十数”的算理由直观的图形语言转化成简洁的数学符号语言：“把45分成40和5，先算40+30=70，再算70+5=75。”