一道2017年高考三角试题的“深度解析”

（山东省滨州市实验中学 山东滨州 256600）

2017年高考数学全国Ⅰ卷理科17题是一道中档解三角题，考查了考生对正、余弦定理及面积公式的综合运用以及运算能力，属于常规的题型。但该题要求考生能对相关公式和定理灵活运用，能从整体上把握已知条件和要求解目标之间的关系。若考生不能对问题的结构特征与数学本质有着深刻的理解，就会面对众多的定理、公式而难以进行正确的选择和变形运用。笔者希望对题目的条件与结论作一番探究，对问题的深层结构进行揭示，提出新的解法，总结解题思路和解题规律。若有不当之处，还请同行们批评指正。首先给出题目：

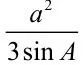
（Ⅰ）求sinBsinC;

（II）若6cosBcosC=1，a=3，求△ABC的周长.

一、解题思路分析

（1）第（I）问的思路分析。

我们要想进行有效的恒等变形，先从已知条件和结论之间的差异入手，条件中是含有边角的等式，结论中只有两角，要想消除之间的差异，就要进行边角的互化。这里因该有两个方向，一个是把条件中的边化成角，与结论相统一；另外一个思路是把角条件和结论中的角都转化成边。

（2）第（II）问的思路分析。

下面先对条件和结论进行一下梳理和变形。

条件有：

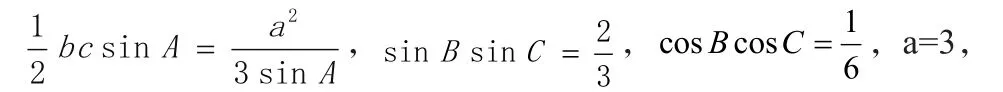
由①②，运用两角差的余弦公式，可求得A=，

结论是求三角形周长，即求a+b+c，又a=3，只需求b+c。

再结合正弦定理，对所求目标进行变形：

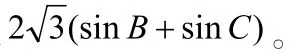
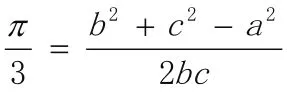
思路一：b c= 8，a=3，cos，三个方程三个未知数，即可得到结论。

思路二：b c= 8，由

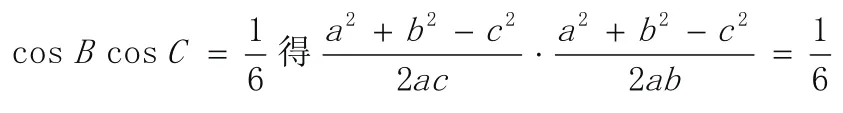
a=3，三个方程三个未知数，求b+c。

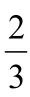
通过上述两个关于B,C方程，

以及sin2B+ c os2B=1,sin2C+ c os2C=1,

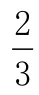
结合上述三个式子，消掉一个角简化运算.

思路五：

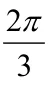
以及由cos(B−C)=cosBcosC+sinBsinC

二、一题多解

第（I）问的解答过程。

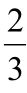
得a=2RsinA,b=2RsinB,c=2RsinC，

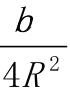
第（II）问的解答过程。

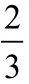
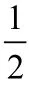
从而

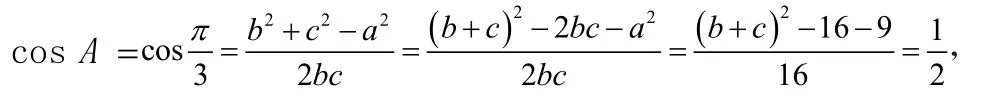
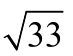
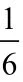
代入bc=8，a=3得(b+c)2(b−c)2=33，

即b4+c4−2b2c2=3,代入b c=8

得b4+c4=161，

再变形得(b2+c2)2−2b2c2=161，代入b c=8

得b2+c2=1 7，

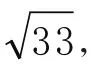
三、反思深化

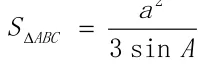
（2）第二问中，解法1和解法2的转化方向都是由角向边进行转化，所用的工具主要是两角和的正弦公式与余弦定理，在转化中需要对“ab”和“a+b”进行整体把握。

（3）我们在平时解题过程中要注意根据题目的已知条件，整体分析已知和所求目标之间的的关系，多一些思考，掌握它们内在的一些联系，时刻注意思维的训练，领悟有关公式变形的数学本质。只有这样我们才能接近问题的深层结构，有助于优化认知结构。