梳理物理综合题中隐性物理现象思维方法例谈

（安徽省南陵县新建初级中学 安徽南陵 242400）

全面认识试题中物理现象是有效解答试题基础，但初中物理综合性试题中，有些物理现象具有隐蔽性，不易被学生观察，成为学生解题难点所在，因此，梳理出试题中隐性物理现象成为突破解题难点的关键，本文列举几例，畅谈物理思维方法在梳理试题隐性物理现象中的有效应用，对例题中学生答题难点和梳理该题隐性物理现象的具体思维过程作简要分析，并从物理思维角度给出该题参考解答。

一、应用因果思维方法梳理出综合题中隐性物理现象

在物理世界里，因果联系是先行物理现象引起后续物理现象的一种必然联系，它是普遍客观存在的，一个物理现象发生，必然有另一个物理现象存在，应用因果思维方法，根据试题中一个物理现象梳理出对应的另一个隐性物理现象，使学生对试题中所包含的物理现象作全面了解，清楚认识试题中物理事件的发生过程。

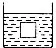
例1：如图1所示，简析浸没杯底塑料块在上升到水面过程中能量转移情况。

学生解题的难点：

本题中，学生不易观察出水的重心位置下移的现象，对水的机械能减少原因不能明确理解，因此对机械能转移的过程解释不清楚。

应用因果思维方法解题思维分析：

本题中两个物理现象，一个是塑料块在液体中上浮，塑料块位置在升高，这个现象比较直观，学生易观察，另一个现象是杯中水的重心在降低，这个现象不具有直观性，不易被学生直接观察，可应用因果思维方法把它梳理出来，即“塑料块位置升高现象”必然导致“上层水位置下移现象”发生，即杯中水的重心在下降，机械能在减少，进而对试题中能量转移的过程有了清楚认识。

参考解答：塑料块位置升高时，导致上层水位置下移，杯中水的重心在下降，水的机械能减少，减少的机械能转移到塑料块上，塑料块的机械能增加。

二、应用逆向思维方法梳理试题中隐性物理现象

物理概念是建立在物理事实基础上，反映的是物理现象和过程本质属性的思维形式，每一个物理概念都对应着本质物理现象，在物理综合性习题中，有些本质物理现象与事物主体之间不是直接联系，具有较强的隐蔽性，应用逆向思维方法，依据试题中主要物理概念，溯源到概念对应的本质物理现象，并梳理出与被研究物体之间的联系，使研究物体有关的隐性物理现象得以显现。

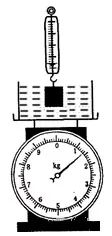
例2：如图2所示，台秤上放着装有适量水的烧杯，弹簧测力计吊着一金属块慢慢放入烧杯中，问弹簧秤和台秤的示数大小怎样变化。

学生解题的难点：

在正常情况下，由于受到基站和ATS中的ProSe服务器共同控制，列车之间的D2D通信的资源分配、流程控制、信令交互都能比较顺利地进行，但是如果通信网络或者ATS系统故障，此时D2D通信可能失去了ProSe服务器的控制，需要额外措施保障行车安全。在通信网络或者ATS系统出现故障的情况下，出于安全考虑，处于故障区域中的列车应启动应急措施，减速或者制动停车并切换为CM(超速防护下的人工驾驶模式)或者RM(限制人工驾驶模式)受人工控制。考虑到出现的故障可能是局部故障，为了兼顾全线的运行，同时还要兼顾故障时列车与现场的反应时间、运营效率以及运行安全，引入列车自组织列车识别与D2D通信方式。

本题中，金属块与台秤不直接接触，金属块对台秤施加力的作用现象具有隐蔽性，进行台秤受力分析时，学生通常只看到水和容器由于自重对台秤施加了力，金属块对台秤发生力的作用现象被忽视，对台秤示数的变化情况也就无法说明。

应用逆向思维方法解题的思维分析：

本题从金属块所受浮力出发，溯源到浮力是“水向上托” 的本质物理现象，就会发现金属块与水之间有相互作用的关系，金属块对水施加了向下的作用力，这个作用力通过水和容器专递给台秤，厘出“金属块对台秤施加了作用力”的隐性物理现象，进而总结台秤示数大小的变化规律。

参考解答：

金属块在水中下降时，与水发生相互作用，对水施加了向下的作用力，这个作用力通过水和容器专递给台秤，台秤受到烧杯、水、金属块三个物体施加力的作用，由于烧杯和水的自重不变，即在金属块没有完全浸没水中前，金属块慢慢放入烧杯过程中，金属块受到的浮力在增加，弹簧秤示数在变小，台秤的示数在变大，当金属块完全浸没水中后，金属块受到的浮力大小不变，这时，弹簧秤和台秤的示数大小都不发生变化。

三、利用物理建模思维方法梳理试题中有特例关系的隐性物理现象

物理模型具有以实物或图片形式直观表达认识对象的特征，物理建模就是根据问题所提供的各种信息， 以抽象分析和形象想象为基本手段， 对事物或过程进行直观处理，最终使物理规律得以显露。在有些物理综合性习题中，各事物物理现象之间联系只具有普遍性，事物之间没有等量关系的特例现象，但用物理建模方法，将有联系的物理现象建构成客观物体模型，在保留原型物理现象本质特征基础上，从中梳理出模型之间有等量关系的隐性物理现象，给解题提供新的思路。

例3：大飞机为了减重，使用了大量新型合金材料。飞机一个合金部件由甲乙两种金属构成，已知甲乙两种金属按质量比2:1混合后的密度与甲乙两种金属按体积比3:4混合后的密度相等，则甲乙两种金属的密度之比为______ 。

学生解题的难点：本题中，学生通常从配比方式的角度去认识飞机零件之间的质量和体积关系，采用合金密度定义的方法来求解两种金属密度的比值：

合金1的密度：

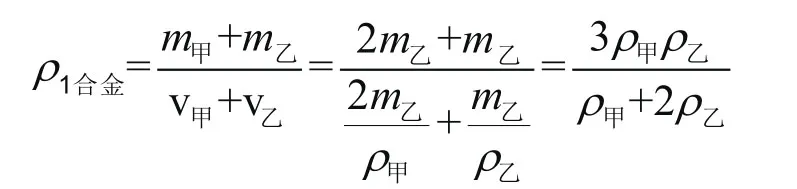
合金2的密度：

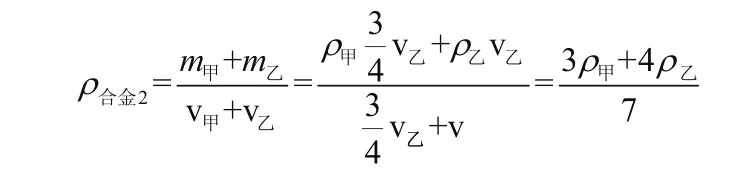
合金1的密度 = 合金2的密度

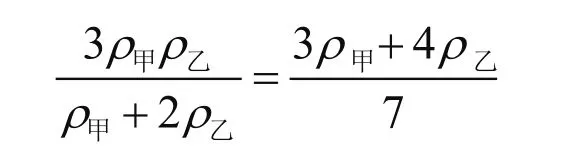
解得甲乙合金密度之比：

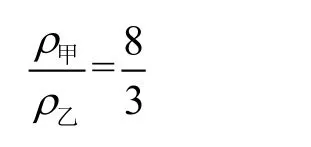
学生解答该题的难点是解题过程复杂，计算量大，用的时间多，解题过程易出错，在心理上产生了畏难情绪。

应用建模思维方法解题的思维分析：

根据题意，将两种配比标准的零件制成实体，从实体零件质量和体积特点去认识两种标准零件之间的质量和体积关系。因为，按照两种配比标准分别制成体积和质量都相等的零件，构成了零件个体之间存在密度、体积和质量都相等的隐性物理现象，将不同标准配比的零件之间质量比和体积比，转换成同种零件内部两种金属之间质量比和体积比，进而将根据“合金密度定义”式求两种金属密度比，间化成由“密度定义”式直接求两种金属密度比。

参考解答：

将试题中两种配比的合金做成体积和质量都相等的相同零件，即这两个零件符合同一个物体的基本特征：质量、体积、密度都相同，即该零件由甲乙两种金属组成，其甲乙两种金属的质量之比为2:1，体积之比为3:4，则甲乙两种金属密度之比：

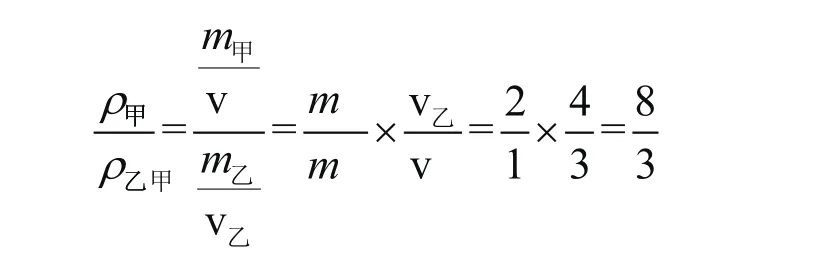
物理思维是有意识的人脑对物理客观事物本质属性、内部规律及物理事物间相互关系间接的、概括的和能动的反映，除具有一般思维特征外，还具有独特的物理研究方法特点，它是是物理学家研究物理问题的基本方法，也是初中生学习物理、解答物理具体问题的科学方法，将其运用到初中物理综合性习题解答中，方法巧妙，能够达到事半功倍的效果。