基于γ变换的Weber-Faces的人脸识别方法

杨 超 伍世虔,2 方红萍

1(武汉科技大学机械自动化学院 湖北 武汉 430081)2(湖北省先进钢铁材料协同创新中心 湖北 武汉 430081)3(武汉科技大学信息科学与工程学院 湖北 武汉 430081)

0 引 言

生物特征识别技术[1](Biometric)克服了传统的身份识别技术[1,3-4]易遗忘、易伪造、安全性低等缺点。由于其独特的性质，被越来越多的科学家和学者们所推崇。人脸识别[5]是生物识别当中的最简单直接高效的一种技术，在主动身份识别和被动视频监控中都有着广泛的应用，特别是在公共安全领域有着独特的优势，为人们提供了便利及安全。虽然卷积神经网络在人脸识别技术中已经发挥了很大的作用[6-8]，但是其学习的时间长，消耗大量资源以及样本的条件无法满足，只能依靠单样本进行识别。但在单样本人脸识别中仍然存在许多问题，如光照、姿态、面部表情、模糊和年龄等[9-10]。特别是光照，人脸识别在室内环境下的应用已经十分成熟，但是在室外环境下，光照条件对人脸识别有很大的影响。

许多经典的人脸识别方法是基于单样本图像本身特征信息的。它们可以简单地分为三类[11]：第一类是传统的图像处理方法，不考虑光照反射模型。例如：直方图均衡化(HE)[12]、Gamma灰度校正(GIC)[13]、各向同性扩散(IS)[14]或各向异性扩散(AS)[14]等。第二类试图进行光照归一化，滤除掉人脸图像的光照部分L，并获得真实的反射人脸R。基于朗伯特反射模型[15-16]，人脸图像上坐标(x,y)点的像素I可以表示为：I(x,y)=R(x,y)L(x,y)。例如单尺度Retinex(Single Scale Retinex,SSR)[17]设计了一个全局的低通滤波器，并在对数域内进行滤波以滤去光照分量L，从而得到反射分量R。自商图像(Self-Quotient Image, SQI)[18]是直接在图像域内通过高斯低通滤波器以商的方式获得反射分量R。韦伯人脸WF(Weber-Faces)[19-20]和多尺度韦伯人脸MSW(Multi Scale Weber faces)[21]都假设局部光照相同，以去除光照L再积分求和获得反射分量R。第三类尝试提取光照不变的特征，利用图像的序特征[22]，提取局部的信息。例如局部二值模式(LBP)[23]是基于序特征在局部邻域内进行二进制编码的一种方法，同时还有其他多种改进方法，例如：拓展局部二值模式(ELBP)[24]，局部三值模式(LTP)[9]，拓展局部三值模式(ELTP)[25]等。

这三类方法并不是完全独立的，近年来，有许多学者将这三类融合在一起进行研究，对人脸图像先进行预处理或光照归一化，再提取它们的特征，以便于识别[9，26]。针对韦伯人脸局部光照相同的假设在光照突变处不适用的问题，提出了一种基于γ变换的Weber-Faces的光照归一化方法。利用γ变换达到局部光照均匀化的目的，再假设局部光照相同，进行Weber-Faces的光照归一化操作，以提高人脸识别率。并且证明了γ变换后的该假设在绝大部分情况下是成立的。最后，提取反射人脸的LBP特征，采用卡方距离和最近邻原则[9]进行识别。在Extend Yale B[27]和AR[28]数据库上进行实验，数据显示，所提出的方法识别率分别为99.08%和99.56%，优于WF和其他方法。

1 光照归一化

1.1 变 换

γ变换是一种常用的非线性变换，用于图像校正，使较亮的区域灰度被压缩，较暗的区域灰度被拉伸增强，图像整体变亮。γ变换的目的是光照均匀化，使局部光照相同的假设更加严谨，以达到更好的光照处理结果和识别效果。为更好地实现变换，首先将图像压缩到0～1的范围内，即：

(1)

根据朗伯特反射模型[15-16]，I=RL，所以有式(1)成立。然后对Ii进行γ变换得到Iγ：

(2)

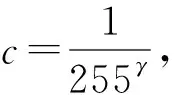
1.2 条件假设

为了消除光照影响，文献[19]假设3×3局部邻域Ω的光照相同，有L(x,y)≈LΩ(x,y)，即导数dL(x,y)≈0。

对于γ变换后Iγ同样为了简化并消除光照影响，假设d(Lγ(x,y))≈0，为了证明该假设更加合理和严谨，下面进行验证。由于WF的假设条件为dL(x,y)≈0，需要证明dL(x,y)≥d(Lγ(x,y))≈0。

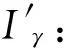
(3)

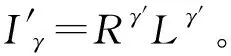
1.3 邻域积分求和

(4)

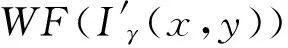
(5)

1.4 处理结果对比

针对人脸识别中光照处理问题，尤其是恶劣的光照条件，图1给出了该方法的光照归一化结果，并对比了几种光照处理的方法，如WF、MSW、SQI、GIC等。如图1所示，(a)表示光照恶劣条件下的人脸图像，(b)到(e)分别为WF、MSW、SQI和GIC对原图(a)的处理结果，而(f)则表示对(e)进行WF的结果。可以很明显地看出，对(a)进行了γ变换的结果(e)的可视性和清晰度改善了许多，局部的光照变得更加均匀，因此，(e)的局部光照相同的假设比(a)更加合理和严谨。所以对(e)进行WF的结果(f)比直接对(a)进行WF的结果(b)好很多，尤其体现在眼睛、鼻子、嘴巴等，同时(f)要优于MSW、SQI。

图1 几种光照处理方法结果对比

2 实验结果

在得到光照归一化的反射人脸r后，直接进行识别会受到位移、微表情等的影响。为了消除这些影响，提取了人脸局部LBP特征，再利用卡方距离和最近邻原则进行识别。为了验证该方法的有效性，在Extend Yale B和AR数据库上进行了实验，并与其他光照归一化方法进行对比，例如LBP、SSR、SQI、GIC、WF、MSW，其参数设置都与文献中所推荐的一致。

2.1 Extend Yale B数据库

Extend Yale B数据库包含38个人的64种光照角度的9种姿势，除去含有损坏图像的7种角度，选取57种光照角度的图像作为测试库，并以正面均匀光照角度(‘A+000E+00’)人脸图像作为训练库。每幅人脸图像的大小为192×168，因此测量直方图的卡方距离时，LBP特征图像被分成24×24块，每个块的大小为8×7。为更好地检验所提方法的性能，提高识别率，采用推荐的σ=1.5，并设置不同的参数α和γ，能够获得在Extend Yale B数据库上更高的平均识别率，如表1所示。可以看出，在α=10且γ=0.7时，平均识别率最高，为99.08%，并在α=10且γ=0.6或0.7时，分别达到99.03%或98.98%，高于WF的识别率98.94%。值得注意的是γ=1时，相当于直接进行WF，唯一不同的是，该方法对式(1)进行压缩导致识别率略微下降。

表1 σ=1.5时，不同γ和α在Extend Yale B上

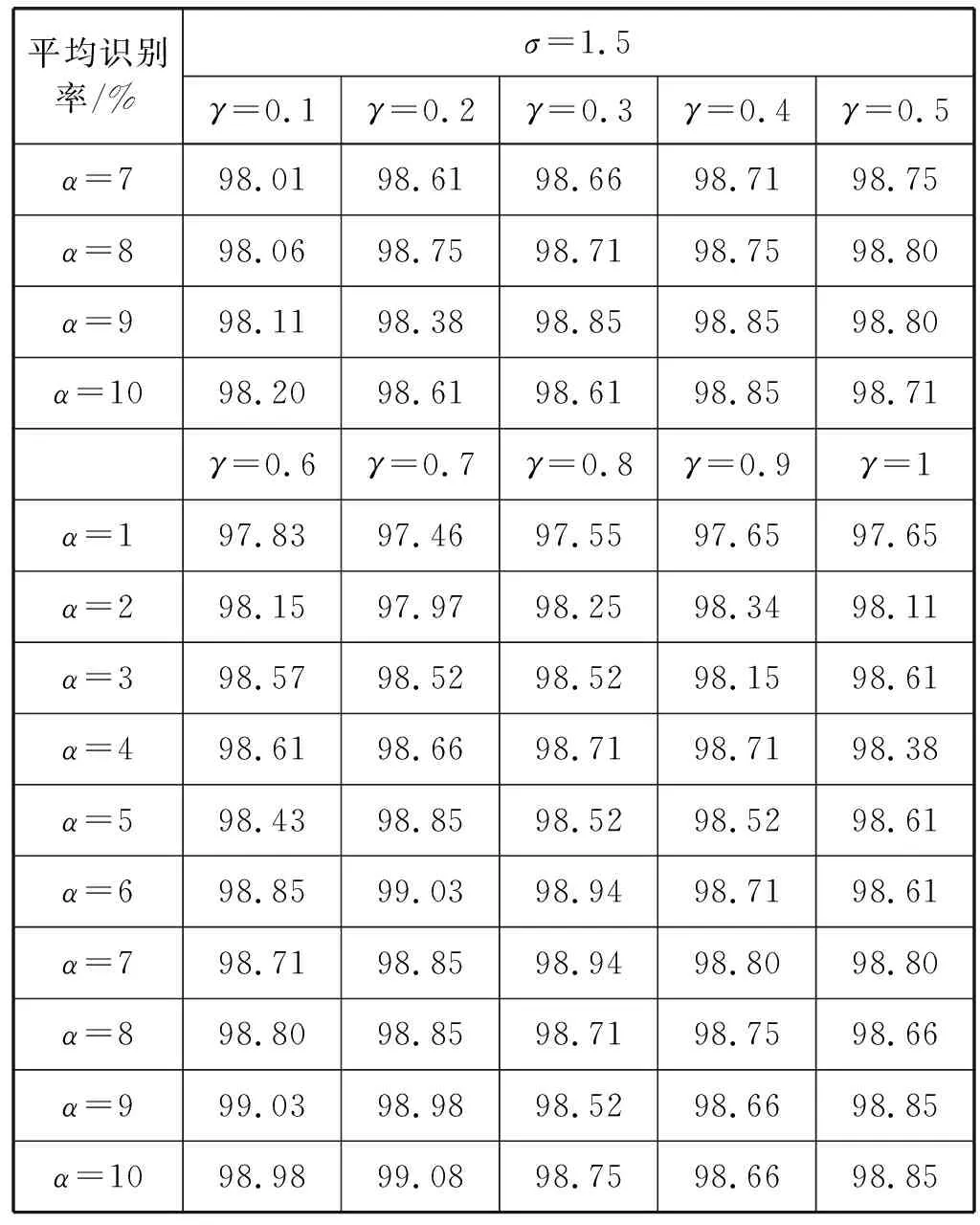
续表1

为进一步比较该方法在不同条件下的效果，根据光照角度将测试库分成五个子集(12°, 25°, 50°, 77°, 90°)[1]，并将其与其他光照归一化方法进行对比，结果如图2所示。可以看出，因为SSR是全局的算法，处理后效果不如直接使用LBP的识别方法。LBP提取的是局部序特征，即大小关系，而GIC不能改变这种局部大小关系，因此其效果与LBP不相上下。这些方法对光照变化的鲁棒性较差，而SQI、WF、MSW以及本文方法都具有很强的光照鲁棒性。其中，本文方法的鲁棒性最高，在光照条件最恶劣的子集5上仍有最高的识别率97.53%，高于WF的96.22%，并且具有最高的平均识别率99.08%，高于WF的98.94%。因为局部光照相同的假设在邻域越大时越不成立，所以MSW的识别率为98.73%，反而比WF略微下降。

图2 几种方法在Extend Yale B的五个子集中的识别率

2.2 AR数据库

AR数据库包含100个人的两个时期，每个时期包含13种图像。由于该方法主要解决光照问题，选取每个时期图像包括：1) 人脸正常光照，2) 人脸左边光照，3) 人脸右边光照，4) 两边光照，5) 戴眼镜，6) 戴眼镜左边光照，7) 戴眼镜右边光照，8) 戴围巾，9) 戴围巾左边光照，10) 戴围巾右边光照。因此有2 000张图像，并将其分为三个子集，并分别以1) 人脸正常光照，5) 戴眼镜，8) 戴围巾作为训练库，相对应的其他光照图像作为测试库。AR人脸图像的大小为165×120，所以LBP特征图像被分成15×15块，每个块的大小为11×8。识别结果对比如表2所示。

表2几种方法在AR数据库上的识别率

识别率/%子集1子集2子集3平均识别率/%LBP98.5099.2510099.25SSR97.8399.2510099.03SQI99.0095.7599.5098.08GIC98.6799.5010099.39WF99.0099.7599.7599.50MSW99.0099.5099.7599.42本文方法99.1799.7599.7599.56

可以看出，在子集3中因为有了围巾的遮挡，且围巾是吸光的，而皮肤是反光的，所以LBP、SSR、GIC达到了100%，高于其他方法。但是在无遮挡的子集1中光照强度变化，本文方法却优于其他方法，LBP、SSR的效果反而下降了。最终，本文方法的在三个子集上的平均识别率最高，达到了99.56%。

3 结 语

针对人脸识别中光照问题，提出了一种基于γ变换的Weber-Faces方法，改进了原始Weber-Faces的条件假设，使其更加合理和严谨，提升了识别效果。实验结果表明，该方法比Weber-Faces具有更强的光照鲁棒性，在Extend Yale B和 AR数据库上，识别率分别达到99.08%和99.56%，优于其他光照归一化方法。