基于小波和多维重构的BP神经网络交通流短时预测
2018-12-13沈钧珥陈作汉
曹 洁 沈钧珥 张 红 侯 亮 陈作汉
1(兰州理工大学计算机与通信学院 甘肃 兰州 730050)2(甘肃省制造业信息化工程研究中心 甘肃 兰州 730050)
0 引 言
随着城市化进程飞速发展,交通拥堵已成为阻碍城市发展的瓶颈,且困扰着市民的出行。有效、合理的短时交通流预测可以为交通管理者和交通参与者提供实时、准确的交通信息,为交通管理和出行选择提供依据。短时交通流预测是交通流预测的一个重要组成部分,是城市交通智能化的重要依据。近年来,国内外众多学者对提高交通流的预测精度展开了深入研究。文献[1]中通过思维进化算法中的“群体寻优”取代“个体寻优”对BP神经网络中的权值和阈值进行优化,对交通流预测精度提高。文献[2]中运用传统的小波固定阈值降噪法对交通流进行降噪处理,再用小波神经网络进行预测,获得较好的预测效果。文献[4]中通过选取一个小波基函数替换BP神经网络中隐含层结点的传递函数来提高预测精度。文献[5]中运用BP神经网络对高速公路进行预测研究。以上研究表明,BP神经网络在识别复杂非线性交通流问题中有着巨大的优越性,但也存在稳定性差、精度容易受到训练数据中噪声影响的缺点。
基于上述分析,本文提出了一种基于小波和多维重构的BP神经网络预测方法。首先选取启发式小波阈值降噪法对交通流数据进行分析、处理,提高交通流数据质量;其次采用C-C方法对交通流数据进行相空间重构,获取多维交通流信息;最后构建多维度BP神经网络模型对短时交通流进行研究分析。
1 交通流数据预处理
由于交通流数据在采集的过程中容易受到各种噪声的影响,导致后期进行预测预测精度较低。小波阈值降噪法能够有效去除数据中的噪声,保留原始特征,且计算简单高效。因此,选用小波阈值降噪法对采集到的交通流数据进行降噪处理。小波阈值降噪是一种建立在小波变换多分辨分析基础上的算法,根据噪声与信号在不同频带上的小波分解系数具有不同强度分布的特点,去除各频带上的噪声信号所对应的小波系数,进而保留原交通流信号中的小波分解系数,然后对降噪后的系数进行小波重构,获取纯净信号。为了能更好的反映出交通流数据特性,本文采用启发式小波阈值降噪法,将有用信号和噪声信号分离,进而提高交通流数据质量。
1.1 小波降噪原理
对于含有噪声的一维信号可表示为:
f(t)=s(t)+δe(t)t=1,2,…,n-1
(1)
式中:f(t)为噪声信号,s(t)为实际数据信号,e(t)为噪声,δ为噪声相关系数,n为信号长度。
具体小波分析运用中,通常近似显示为低频信号或为相对平稳的信号;细节则表现为高频信号,噪声分量一般集中于高频信号中。小波降噪的基本过程为:先对含有噪声信号小波变换的分解,选择分解层数为4层进行阐述,经分解后的信号其噪声部分分量通常在cD1、cD2、cD3、cD4中,cD及cA分别为信号经小波变换分解后的细节系数和近似系数,接着对细节系数cD分量采取适当的阈值实行降噪,最后通过将降噪后的近似系数cA以及各层细节系数cD进行重构,从而得到降噪后的信号。
1.2 启发式小波交通流降噪
小波降噪阈值的选取是提高小波降噪能力的关键,目前常见的小波阈值选择方法有:固定阈值估计(Sqtwolog)、极值阈值估计(Minimaxi)、无偏似然估计(Rigrsure)以及启发式估计(Hesusure)等。极值阈值估计和无偏似然估计方法只能对低频段的噪声信号有着较好的降噪效果,且极值阈值估计降噪时间较长。而启发式阈值估计是将固定阈值估计和无偏似然估计相结合起来,能够获取最佳的预测效果,其步骤为:
Step1一维信号的小波分解。选择合适小波基函数,对一维信号f(t)进行N层分解。
Step2高频系数cD的阈值量化。设定阈值标准,对分解后得到的cD进行量化处理,阈值量化的效果直接影响降噪的效果。固定阈值为:
(2)
无偏风险阈值方法主要是由Stein无偏似然估计原理所估计出的最小风险量所对应的小波系数确定自适应阈值。其原理为:
通过将信号f(t)中各个元素取绝对值后平方,再由小到大排列,进而得到以下新的信号序列,即:
f(k)=(sort(|f|))2k=0,1,…,N-1
(3)
取阈值f(k)的第k个元素的平方根,即:
(4)
则该阈值产生的风险:
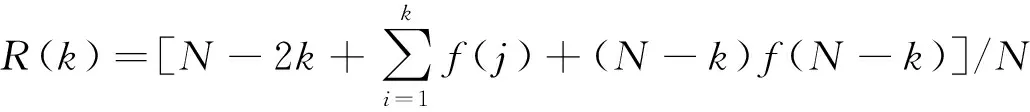
(5)
根据R(k),寻找最小风险点所对应的kmin值,其Rigrsure的阈值则定义为:
(6)
假设信号f(t)长度为N,通过无偏似然估计和固定阈值方法分别得到的阈值,令:
(7)
(8)
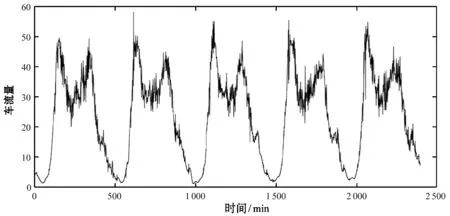
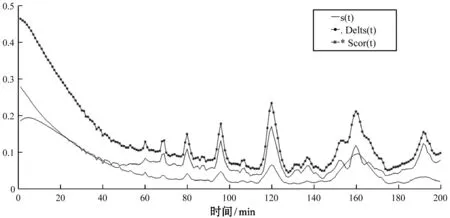
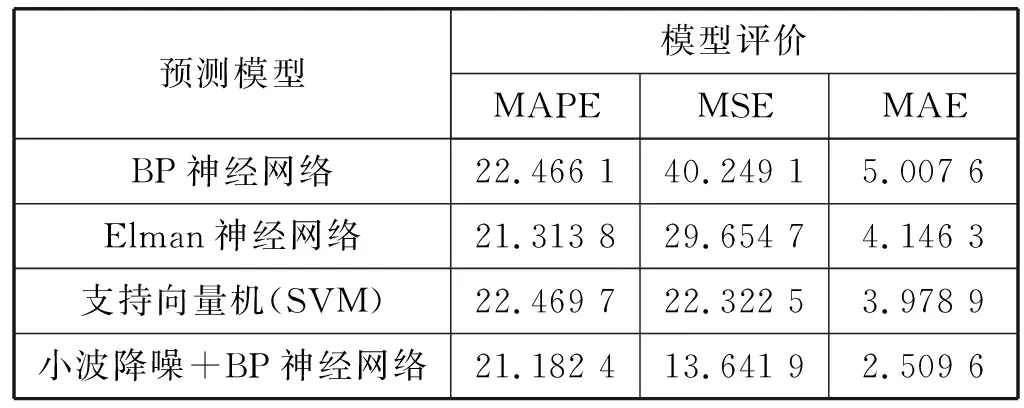
若eta Step3一维信号的恢复。将启发式阈值量化后的高频系数cD与小波分解的第N层低频系数cA进行重构,获取降噪后的信号。 交通流作为典型的混沌时间序列,具有较强的非线性。本文运用C-C法对所用交通数据进行重构,映射出交通数据中的多维信息。为了体现交通流是否具有短期预测性,本文在相空间重构的基础上,选用小数据量法计算得到交通流的最大李雅普诺夫(Lyapunov)指数,进一步对具有混沌特性的短时交通流进行特定分析。 运用检测器、摄像头等所采集的实时交通流数据呈现一维时间序列,无法准确地反映出交通流复杂特性。因此,将一维交通流时间序列扩展为多维交通流时间序列显得极为重要。对一维交通流时间序列x(t1),x(t2),…,x(tn)进行相空间重构,得到多维时间序列: x(ti) = [x(ti),x(ti + τ),…,x(ti + (m-1)τ)] (9) 式中:时间延迟为τ,嵌入维数为m,以及相点数为x(ti),i=1,2,…n-(m-1)τ。 由式(9)可得,时间延迟τ以及嵌入维数m的确定是相空间重构的关键。经研究表明,时间延迟τ、嵌入维数m以及相空间重构中的时间窗宽τw这三者之间存在一定的联系,Kugiumtzis曾提出延迟时间τ嵌入维数m以及时间窗宽τw它们都不是独立地存在,三者存在一定的相互关系tw=(m-1)τ[8]。本文运用C-C法来实现多维交通流时间序列的提取,其具体步骤如下: Step1获取一维时间序列数据,计算时间序列的标准差δ,将交通流数据重新分解为t个不相交的时间序列,确定N。 Step2当N→∞时,计算s(m,r,t)和ΔS(m,t),其中时间变量t⊂[1,200] : (10) m=[2,5] ΔS(m,t)=max{S(m,r,t)}-min{S(m,r,t)} (11) Step3计算下列三式: (12) (13) (14) Lyapunov指数是检验系统是否存在混浊现象的重要特征量,文献[9]等研究表明,最大Lyapunov指数可用来描述系统运动对初始条件的敏感性。若获取的最大Lyapunov指数大于零时,则表明该交通流时间序列具有混沌特性,可以进行短时交通流预测。 通常计算最大Lyapunov指数有很多的方法,如:Wolf法、Jacobian法、P-范数法以及小数据量法等。小数据量方法计算量小、计算精度高、相对容易操作,在识别混沌特性方面具有一定的优越性。其具体步骤: Step1对时间序列{x(ti),i=1,2,…,N}进行FFT变化,获取时间序列平均周期。 Step2运用C-C法获取时间延迟τ和时间窗宽τw,计算得到嵌入维数m,并进行相空间重构{Yj,j=1,2,…,M}。 Step3寻求相空间中每个点Yj所对应的最近邻近点Yj′并进行相分离,即: (15) Step4计算相空间中最近邻近点Yj′所对应的i个离散时间步间的距离dj(i): dj(i)=|Yj+i-Yj′+i| (16) 式中:i=1,2,…,min(M-j,M-j′)。每个i求出所有j的Indj(i)的平均y(i),即: (17) 式中:q表示dj(i)不为零的个数,运用最小二乘法做出回归直线的斜率就是最大Lyapunov指数。 BP神经网络是由信号向前传递、误差反向传播的一种双向传递的多层前馈神经网络。它具有强大的适应能力,能够自行的挖掘出数据中的潜在规律,其主要由输入层,隐含层以及输出层构成,基本结构图如图1所示。 图1 BP神经网络结构图 信号前向传播和误差反向传播是BP神经网络最基本的两个部分。具体如下: Step1前向传播:获取BP神经网络隐含层输入xj的所有输入个数的加权和,即: (18) Step2误差反向传播:反馈误差按梯度下降学习方式对各层权值及阈值进行修正,使网络预测输出不断逼近期望输出。 (19) BP网络误差性能指标函数为: (20) 输出层与隐含层之间的权值为: (21) 式中:η为学习率,η⊂[0,1]。 更新输出层与隐含层间的权值: (22) 输入层与隐含层间的权值wij的学习算法: (23) 更新输入层与隐含层间的权值: (24) BP神经网络主要是通过不断的迭代进行参数择优,一次完成的训练包括信号的前向传播以及误差反向传播。通过参数调整达到最优的训练网络,输入测试数据,获得相应的结果。 本文研究所用数据源于明尼苏达大学交通实验室平台所公布的交通流数据。通过100个检测器获取2016年1月1日-2016年1月5日的数据,如图2所示,数据采样周期以3分钟为准,每天获取480个数据,5天总获取2 400个数据。为了能使预测误差减小,采用函数mapminmax将预测数据处于[0,1]之间。 图2 原始交通流量 为了能更好地消除交通流数据中产生的高斯白噪声,选用启发式阈值进行降噪处理。通过实验发现5层小波分解使得数据过于平滑,不能反映出交通数据中所隐藏的信息。因此,为了能更好地反映交通流数据的原有特征,则使用小波工具箱中的sym8小波函数进行4层分解、降噪、重构。降噪效果如图3所示。通过对比可得降噪后的数据显得更加平滑。 图3 小波降噪交通流量 实验获取交通流时间序列的长度为2 400,计算交通流量时间序列的标准差:取2≤m≤5,0.5σ≤r≤2σ,1≤t≤200。通过C-C法得到3个统计量分别为s(t)、delt_s(t)、s_cor(t),其中s(t)为所有子序列的统计量S(m,N,r,t)的均值。时间延迟τ由delt_s(t)的第一个局域极小值点所对应的时间所决定;τw是通过s_cor(t)的全局最小值所对应的时间来确定。通过图4所示,当t=34时,delt_s(t)取得第一个局域极小值,因此可以得到τ=34。从s_cor(t)曲线中可得,当t=128时取得全局最小值,则τw=128。通过公式τw=(m-1)×τ可得m=4.764 7,本文进行相空间重构时取整数m=5,通过公式M=N-(m-1)×τ可以得出相空间点为2 264。运用小数据量方法获得的最大Lyapunov指数λ=0.016 83,反映出重构后的交通流时间序列具有混沌特性,因此交通流具有较好的短时预测性。 图4 多维交通数据参数关系图 通过检测器获得2 400组数据,根据C-C方法估算得到嵌入维数和延迟时间。经相空间重构后,任意选取相空间点中75%相点进行BP神经网络模型训练,25%相点作为BP神经网络预测。 图5显示未经启发式小波降噪的BP神经网络预测结果;图6显示 Elman神经网络预测结果;图7显示小波降噪+多维BP神经网络预测。通过对比显示,本文的预测方法结果能更好的反映出交通流变换特性。 图5 BP神经网络预测结果 图6 Elman神经网络预测结果 图7 小波降噪+多维BP神经网络预测 为了能更好地显现出短时交通流模型的优越性,本文选用平均相对误差、均方误差以及平均绝对误差等进行预测评估。 平均相对误差: (25) 均方误差: (26) 平均绝对误差: (27) 式中:Yyeat(t)表示在t时刻的交通流量的实测值;Ypred(t)表示预测值,N为样本个数。 MAPE的值反映预测值与实际值的偏离程度,MAPE越小,则显示预测值与实际值偏离程度小且预测效果越好;通过MSE的值来反映误差分的分布情况,MSE值越小,误差分布就越集中且预测效果就越好。表1为误差对比。 表1 实验误差对比 通过以上对比分析可得:运用Elman神经网络、支持向量机(SVM)以及本文所提出的方法,在所预测的时间段历史数据库有着较好的相似度,但运用本文的方法均方误差最低,达到2.509 6,且随着交通流数据中噪声的降低,以及交通流的突变性减弱,预测精度得到了进一步的提高。 通过启发式阈值降噪实现交通流数据分层降噪有利用充分去除交通流数据中的噪声,大幅度提高数据质量,进而提高预测精度;选用C-C法实现交通流多维信息的获取,更加充分反映交通流变化轨迹,并进一步确定了BP神经网络输入层个数;最后通过BP神经网络模型预测。通过实验误差对比,文中所运用的方法使均方误差从40.349 1降低到13.641 9,能更好地反映出交通流非线性。但由于单个BP神经网络模型泛化能力低,具有一定的随机误差性,下一步结合Bagging集成算法对短时交通流预测展开更加进一步的研究。2 交通流多维度信息提取
2.1 交通流相空间重构
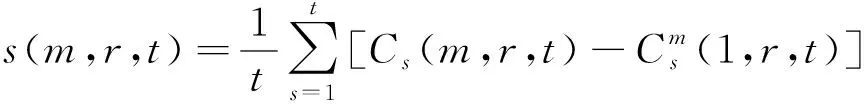
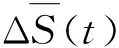
2.2 交通流可预测性分析
3 多维BP神经网络预测模型
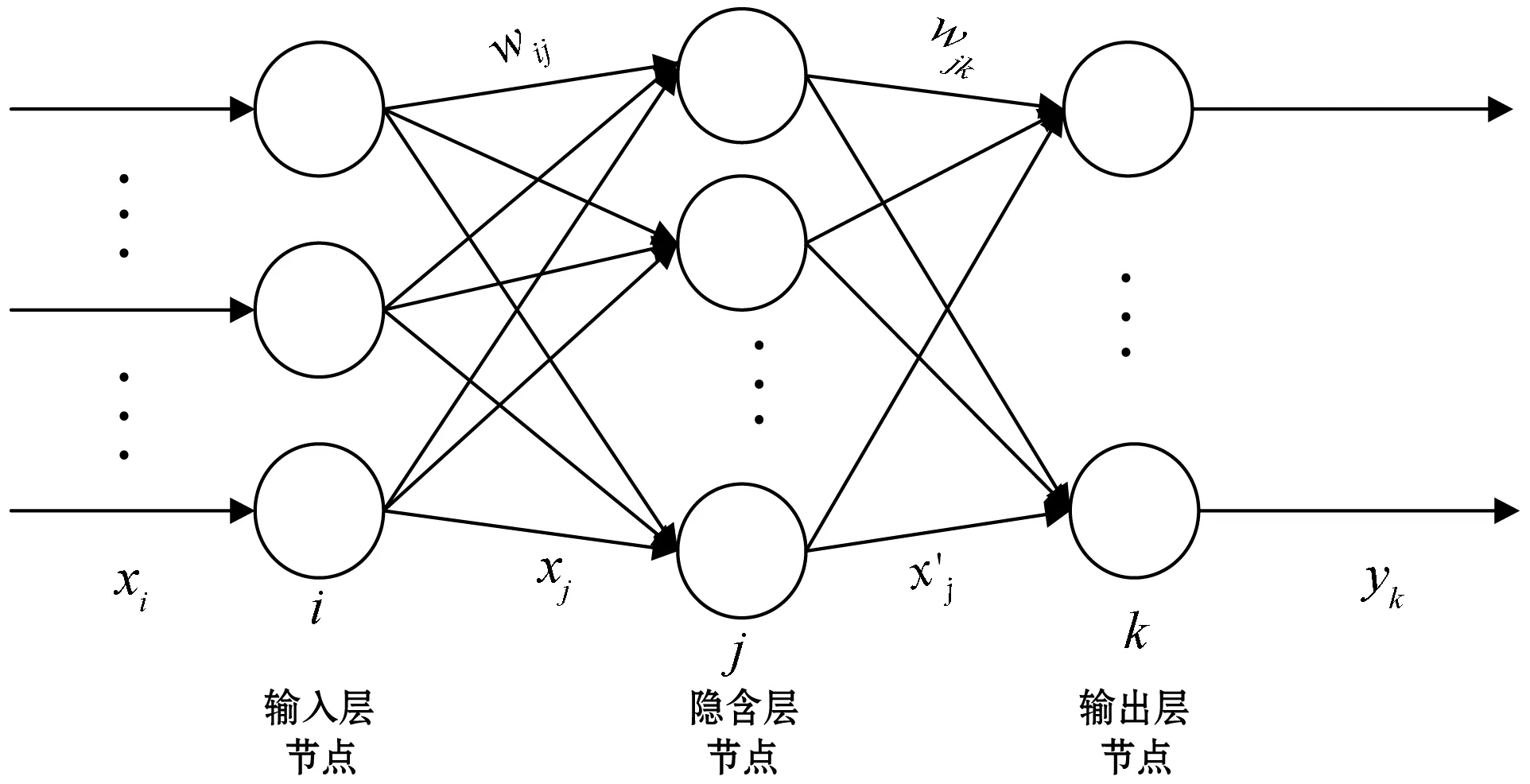
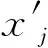


4 实验与分析

4.1 交通流数据预处理
4.2 交通流数据空间重构
4.3 多维BP神经网络预测
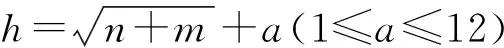



4.4 交通流预测模型评价
5 结 语
