基于相似日聚类与支持向量机的迎峰度夏期间负荷预测方法

杨方圆 ，包 丹，张明理，邓鑫阳，张 娜

(1.国网辽宁省电力有限公司经济技术研究院，辽宁 沈阳 110010；2.国家电网公司东北分部，辽宁 沈阳 110180)

日负荷曲线是电力公司调度部门制订调度计划，安排发电机组开停机组合、经济分配发电机组的有功出力及决定系统调峰容量的基础。因此，研究如何实现日负荷曲线的精准预测对提高电力系统经济效益有着重要的意义。

目前，传统的短期负荷预测分析方法已不能满足电力供需[1-10]精准预测的要求，急需提高电力需求方法的预测精度。文献[11]提出基于负荷混沌特性和最小二乘向量机的短期负荷预测模型，通过相空间重构与训练决策函数，避免了传统人工网络法容易陷入局部极值的问题。文献[12]提出了基于联合灰色模型和最小支持向量机回归的电力短期负荷智能组合方法，通过机器学习确定所选单一模型的权重因子，克服了传统组合模型中设定权重因子的困难。文献[13]通过对模型关键参数的自适应动态寻优，避免了最小支持向量机对设计者经验的过度依赖以及选择模型参数时缺少科学依据的局限性。

本文建立基于K-means聚类算法与支持向量机的短期负荷预测模型。支持向量机的计算结果通常取决于少数的几个关键样本，采用聚类算法筛选出与待测日最相似的样本训练集，在不影响支持向量机泛化能力的先决条件下有效地降低算法的复杂程度，预测结果具有较高的精度。采用以上方法对辽宁电网迎峰度夏期间的日负荷曲线进行预测，算例结果证明了该方法的有效性。

1 负荷预测的基本框架

1.1 Κ-means聚类算法

Κ-means聚类算法的基本原理：首先选取聚类数目k以及任意确定k个初始类簇中心点，计算每一个样本点与k个初始类簇中心点之间的欧式距离，按最小欧氏距离的原则对所有样本类型进行分类。反复计算类簇中心点，不断调整样本的分类，直至各样本到所属类簇中心点之间的距离平方和达到最小。

Κ-means聚类算法具有化繁为简、快速高效的优点，适合于巨量数据的聚类分析。该算法的缺陷是聚类数目k具有不确定性，如果聚类的数目设定不合理，将难以获得优良的聚类效果。

1.2 最优聚类数目的确定算法

聚类的目标是通过选取最优的聚类数目k，使得所有样本的聚类生成簇实现最优良的效果。通常情况下，希望获得类内成员紧密、类间成员远离的最佳聚类结构。为了获得最优的聚类数目k，通常采用聚类有效性指标来度量聚类算法生成簇的结果。目前，已有文献中的聚类有效性指标难以获得准确的最优聚类数，本文针对该问题设计了一种基于调整余弦相似度的新的Κ-means聚类算法有效性指标，该指标可以对聚类算法划分结果的质量进行评价，从而获得最优聚类的数目k。

定义1：令待聚类的样本数据空间为X={x1,x2,…，xn}，假设n个样本对象聚类为m类，定义第j类的第i个样本与类间样本的最小调整余弦相似度平均值为ic(j,i)，即：

(1)

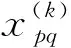
定义2：令待聚类的样本数据空间为X={x1,x2,…，xn}，假设n个样本对象聚类为m类，定义第j类的第i个样本与类内样本的调整余弦相似度平均值为为ac(j,i)，即：

(2)

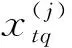
定义3：令待聚类的样本数据空间为X={x1,x2,…，xn}，假设n个样本对象聚类为m类，定义第j类的第i个样本的聚类有效性指标为最小类间调整余弦相似度平均值与类内夹角调整余弦相似度平均值之和、最小类间调整余弦相似度平均值与类内调整余弦相似度平均值之差的比值IACR(j,i)，见式(3)。

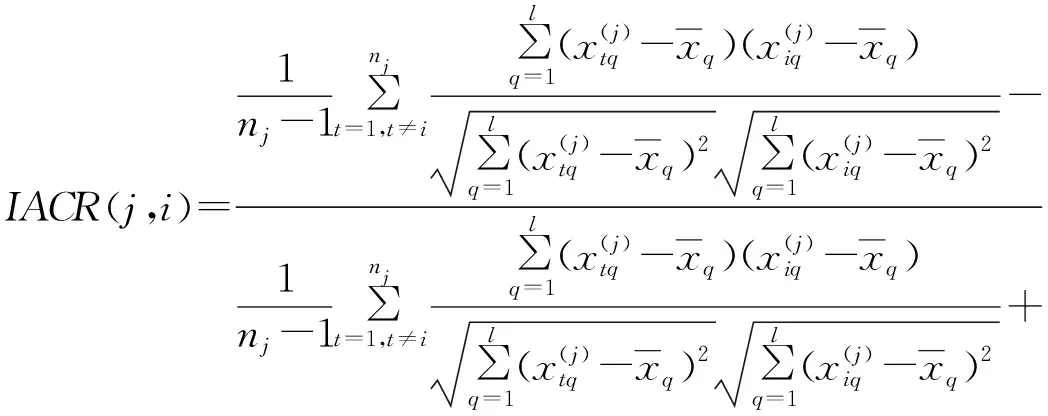
(3)

IACR指标可以反映出数据集内某个样本的聚类效果。本文通过计算聚类空间内所有样本的IACR(j,i)指标的平均值来研究数据集的聚类质量，计算方法如式(4)所示。希望聚类生成簇后获得类内成员尽可能紧密、类间成员尽可能分散的最优聚类结构，如式(5)所示，当IACR取最大值时对应的聚类数目为最优聚类数目。

(4)

(5)

1.3 支持向量机算法

该算法是基于结构风险最小化原理的通用学习方法[14]，适合于解决非线性空间的小样本问题。支持向量机通常通过目标极小值优化模型来确定回归函数：

(6)

(7)

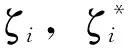
通过求解式(7)可以得到回归函数：

(8)

2 选择日负荷曲线的相似日

2.1 Κ-means聚类算法选取相似日

选取日负荷曲线相似日的流程如图1所示。

2.2 日特征向量

短期负荷预测存在一定规律，即相同日类型的负荷具有相似性。考虑到工作日与节假日的负荷特性存在差异，将日类型分为工作日与节假日两类。为准确反映出气象因素对负荷的影响，选取每天的整点气温、湿度、风速作为日特征向量。本文对日类型进行初步筛选后，将日特征向量作为聚类分析的样本。

3 算例分析

结合辽宁电网的日负荷曲线历史数据及气象局提供的气象特征参数历史数据，采用聚类分析与支持向量机结合的算法对日负荷曲线进行预测。通过聚类算法选取相似日，充分考虑温度、湿度、风速和日类型等参数的影响，利用支持向量机对辽宁电网的日负荷曲线进行预测。

以辽宁省的气象数据为自变量，辽宁电网24 h负荷值为因变量，对2017年6月1日—8月17日的气象历史数据及预测日的气象特征参数值进行聚类分析，确定最佳聚类数目，相似聚类效果如图2所示。利用本文所介绍的方法对辽宁电网2017年8月18日负荷曲线进行预测，预测值与真实值的比较结果如图3所示。

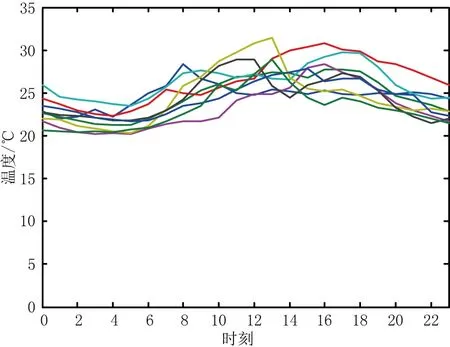
图2 相似日聚类结果

图3 预测日负荷的真实值与预测值比较

为了验证本文方法的适用性与有效性，将传统支持向量机与本文方法的预测效果进行比较，计算得到辽宁电网迎峰度夏期间的负荷预测结果如表1所示。采用本文方法计算得到2017年8月18—27日的负荷预测值，预测结果的平均相对误差均低于3%，均方根误差均低于3.5%。根据表2可知，采用本文的算法训练样本的数目明显减少，当聚类数目为6，筛选后的支持向量机训练样本为384个，所需的训练时间为传统支持向量机算法的1/5。与传统的支持向量机算法相比，本文提出的方法复杂程度明显减弱，在迎峰度夏期间日负荷曲线的预测精度平均提高1.6%，实现良好的预测效果。

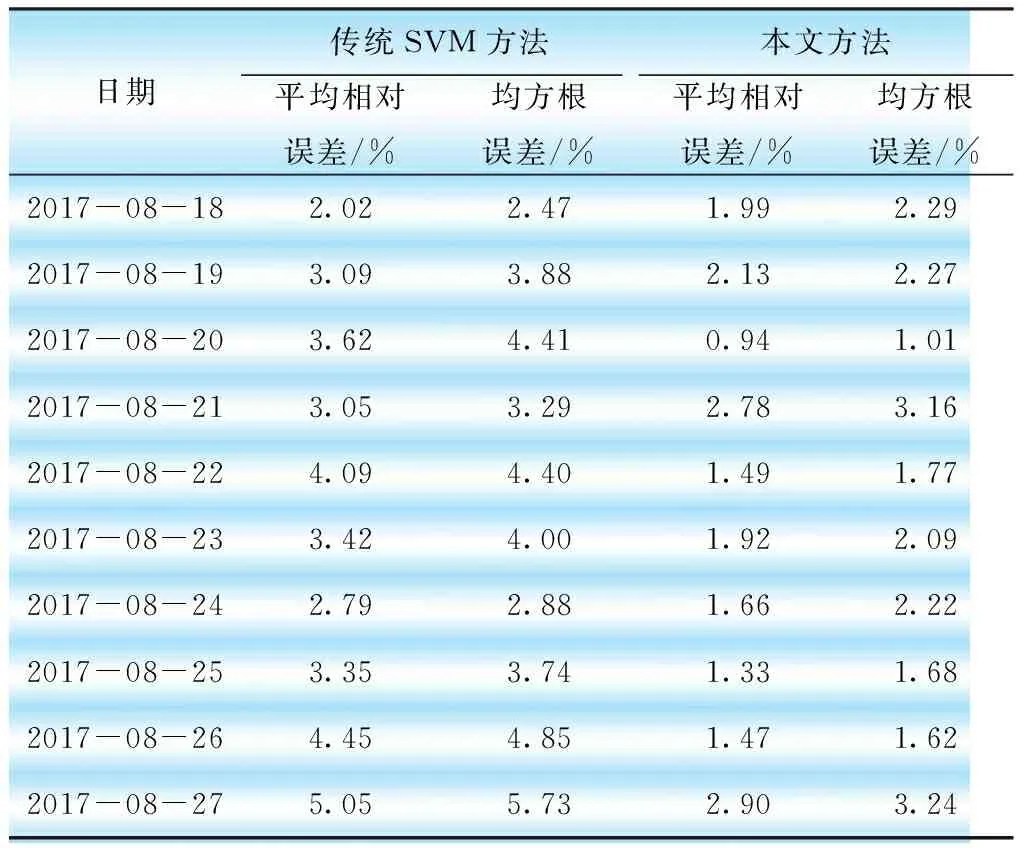
表1 负荷预测误差比较

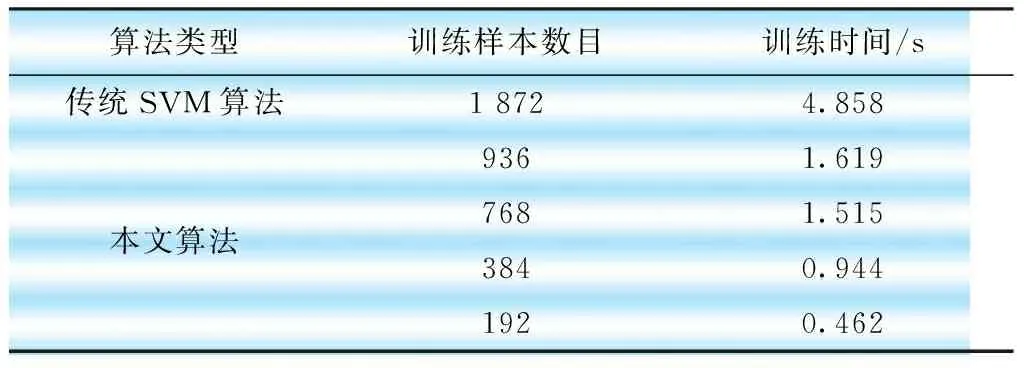
表2 本文算法与传统支持向量机算法训练速度的对比

4 结束语

本文提出一种相似日聚类算法与支持向量机算法结合的迎峰度夏期间负荷预测方法。此方法融合聚类算法与支持向量机两者的优势，实现优势互补。利用辽宁电网迎峰度夏期间的日负荷曲线进行建模验证，采用本文方法得到的日负荷曲线预测值，平均相对误差在3%以内，样本训练的时间也大幅减少。该算例证明了本文预测方法的适用性与有效性。