海洋钻井天车升沉补偿系统不同摇摆装置性能分析

刘振东,张彦廷,黄鲁蒙,陈 帅,王 康,牟新明

(1.中国石油大学(华东)机电工程学院,山东青岛 266580; 2.中国石油宝鸡石油机械有限责任公司,陕西宝鸡 721002)

在海浪的作用下,浮式钻井平台在深海作业时会产生升沉、艏摇、横摇、纵摇、橫荡、纵荡6个自由度的运动[1-3]。为克服平台升沉运动对钻进工作的影响,浮式海洋钻井平台上必须配备一套钻柱升沉补偿系统[4-7]。目前常用的钻柱升沉补偿系统种类较多,其中天车升沉补偿系统因具有占用甲板面积小、补偿率高、无需两条活动的高压油管等诸多优点得到了广泛应用[8-10]。为保证浮动天车相对钻井平台运动时钢丝绳始终处于张紧状态,天车升沉补偿系统均设计有一套摇摆装置。渠迎峰等[11-12]完成了天车升沉补偿系统的摇摆臂长度及滑轮固定点位置设计、补偿用复合缸结构及最佳位置确定、主管路隔离阀设计等研究工作;刘清友等[13]设计了一套利用电机驱动齿轮齿条机构带动浮动天车在既定直线轨道内上下运动的新型天车升沉补偿方案,并开展了传动分析和齿轮啮合力计算;徐涛等[14-15]设计了一套利用液压缸支撑摇摆装置中间滑轮的方案,并开展了运动规律分析。天车升沉补偿系统摇摆装置的钢丝绳缠绕方式、摇摆臂长度对摇摆臂受力、钢丝绳使用寿命及升沉补偿效果均有重要影响,但是目前尚未开展相关研究[16-17]。笔者针对3套典型的天车升沉补偿系统摇摆装置方案建立数学模型,开展摇摆臂受力、钢丝绳窜绳长度、钢丝绳直弯交变长度等方面的数值分析,并基于线性加权和法对3套方案进行综合评价。

1 现有典型方案

目前常见的天车升沉补偿系统钢丝绳缠绕方式可分为内绕式和外绕式两种,分别如图1所示。

图1 钢丝绳内绕式和外绕式天车升沉补偿系统Fig.1 Crown-block heave compensation system with inner enwinding wirerope and outer winding wirerope

采用内绕方式时,钢丝绳活动端先通过滑轮B的内侧,再经过滑轮C和滑轮A的外侧,钢丝绳与下摇臂BC交叉,与上摆臂AC平行。采用此缠绕方式,滑轮B距离天车升沉补偿系统中心位置较近,与钻机相连接的结构比较紧凑。

采用外绕方式时,钢丝绳活动端依次从滑轮B、C、A外侧通过,与下摇臂BC和上摆臂AC平行。为保证滑轮B能够起到良好的导向作用,要求滑轮C始终要处于滑轮B的右上方,因此滑轮B距升沉补偿装置中心位置较远,与钻机相连接的结构比较庞大。

通过调研国内外现有天车升沉补偿系统的技术资料,选取出3套典型方案进行分析,其主要参数如表1所示。

表1 典型天车升沉补偿系统主要参数

表1中,偏置e为滑轮A与滑轮B的水平中心距;夹角ψ为钢丝绳与下摇臂BC之间的夹角,取决于下摇臂长度a和滑轮直径D;夹角θ与夹角ψ互为余角;ω为下摇臂BC与上摆臂AC之间的夹角。

2 摇摆臂受力数值分析

2.1 内绕式

2.1.1 数学模型建立

以滑轮C中心为原点建立直角坐标系,与下摇臂BC垂直向右为x轴正方向,沿下摇臂BC向上为y轴正方向,滑轮C受力如图2所示。

建立平衡方程并进行归一化处理可得:

(1)

(2)

式中,FS为钢丝绳拉力,kN;Fyb和Fbb分别为下摇臂和上摆臂对滑轮C的支撑力,kN。

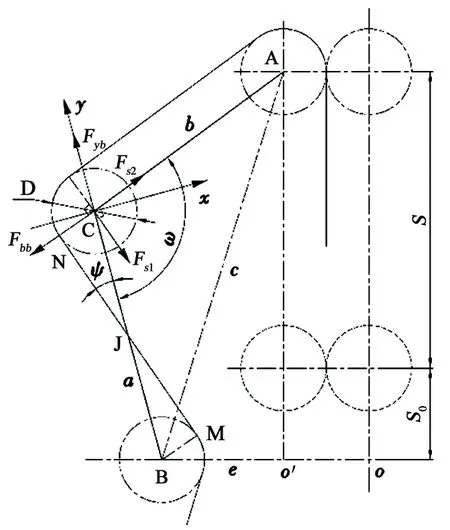
图2 内绕式方案滑轮C受力图Fig.2 Force diagram of pulley C in inner enwinding scheme

距离S与ω之间的关系为

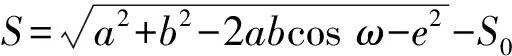
(3)

2.1.2 数值计算结果

建立式(1)、(2)的simulink程序框图,分别将方案Ⅰ、Ⅱ的参数ψ和ω输入到程序框图中,可求得Fyb/Fs和Fbb/Fs随ω变化的趋势如图3所示。

从图3可以看出:①下摇臂支撑力Fyb随ω增大而逐渐增大,两端增速较快,中间部分增速较缓。②上摆臂支撑力Fbb随ω增大先减小后增大,两端变化速率较大,中间部分变化较缓。当ω等于90°时Fbb最小。

图3 内绕式方案摇摆臂受力随ω变化规律Fig.3 Force variation rules of swing arms with ω in inner enwinding scheme

建立式(3)的simulink程序框图,分别将方案Ⅰ、Ⅱ的参数a、b、e和ω输入到程序框图中,结合图3可得Fyb/Fs和Fbb/Fs随S变化的趋势如图4所示。

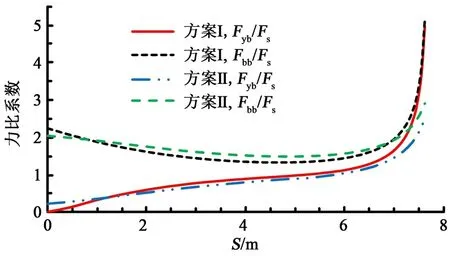
图4 内绕式方案摇摆臂受力随S变化规律Fig.4 Force variation rules of swing arms with S in inner enwinding scheme

从图4可以看出:①方案Ⅰ下摇臂支撑力Fyb随S增大先是基本呈线性增加,临近结束时增速陡然增加,其中最小力比系数为0.01,最大力比系数为4.95,平均力比系数为1.32;方案Ⅱ下摇臂支撑力Fyb随S增大前期变化趋势与方案Ⅰ基本相同,临近结束时增速有所增加,其中最小力比系数为0.24,最大力比系数为2.50,平均力比系数为1.08。②方案Ⅰ上摆臂支撑力Fbb随S增大先是基本呈线性减小趋势,然后减速变缓,临近结束时增速陡然增加,其中最小力比系数为1.33,最大力比系数为5.15,平均力比系数为1.94;方案Ⅱ上摆臂支撑力Fbb随S增大前期变化趋势与方案Ⅰ基本相同,临近结束时增速有所增加,其中最小力比系数为1.49,最大力比系数为2.90,平均力比系数为1.82。

2.1.3 对比分析

方案Ⅰ和方案Ⅱ虻的下摇臂、上摆臂受力变化规律基本一致,但方案Ⅰ下摇臂的最大支撑力为方案Ⅱ下摇臂最大支撑力的2倍,方案Ⅰ上摆臂的最大支撑力为方案Ⅱ上摆臂最大支撑力的1.78倍,因此方案Ⅱ摇摆臂受力状态较好。

2.2 外绕式

因外绕时钢丝绳方向始终与下摇臂、上摆臂平行,故下摇臂和上摆臂均为二力杆,在平衡状态下,Fyb=-FS1,Fbb=-FS2,即下摇臂、上摆臂支撑力始终与钢丝绳拉力大小相等,方向相反。

与内绕式相比,钢丝绳外绕时下摇臂、上摆臂支撑力较小,且无交变载荷,受力状态较好。

3 钢丝绳工作状态数值分析

3.1 内绕式

3.1.1 数学建模

内绕式钢丝绳在A、B、C三个滑轮处的包角如图5所示,滑轮B处包角为α1+α2,滑轮C处包角为β1+β2,滑轮A处包角为γ1。

图5 内绕式钢丝绳包角分析Fig.5 Wrappingangle analysis of inner enwinding wirerope

根据几何定理可知,β2+γ1≡180°,α1=β1,故钢丝绳在A、B、C三个滑轮处的总包角为∑Gbj,表示为

∑Gbj=180°+2α1+α2.

(4)

α2取决于滑轮B与钻机主绞车的相对位置,在升沉补偿过程中保持不变,假设为15°。

根据余弦定理可得

(5)

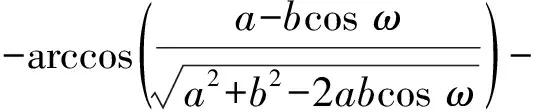
(6)

3.1.2 数值计算结果

建立式(5)、(6)的simulink程序框图,分别将方案Ⅰ、Ⅱ的各项参数输入到程序框图中,可以得到α1、β2随ω的变化趋势如图6所示。

图6 内绕式方案α1、β2随ω变化规律Fig.6 Variation rules of α1 and β2with ω in inner enwinding scheme

从图6中可以看出:①α1先随ω增大快速增加;当ω为60°时,α1接近最大值;然后α1随ω增大逐渐变小。②β2先随ω增大快速减小,当ω大于60°后β2减小速度减缓,然后基本呈线性减小趋势。

结合式(3)和图6可得α1、β2随S的变化趋势如图7所示,可以看出:①α1先随S增大而逐渐增大,然后再逐渐变小;②β2随S增大基本呈线性减小趋势;两端减小速率较大,其中方案Ⅰ的β2减小速率大于方案Ⅱ的。

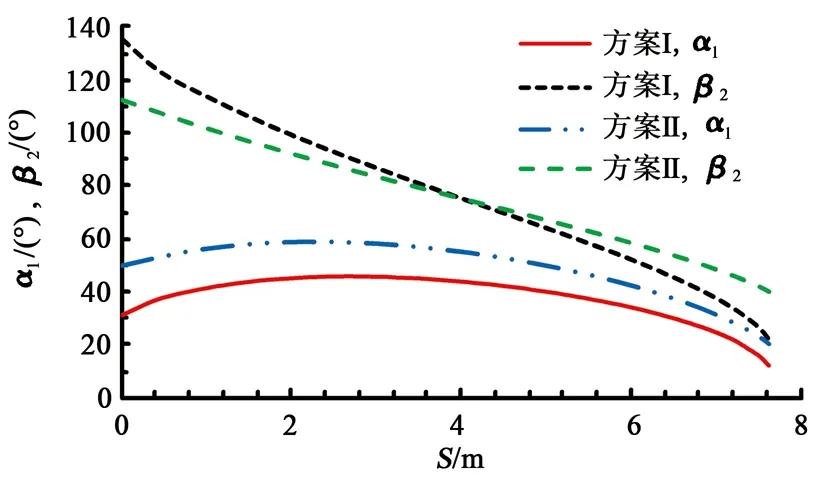
图7 内绕式方案α1、β2随S变化趋势Fig.7 Variation rules of α1 and β2with S in inner enwinding scheme

3.1.3 窜绳长度分析

假设在升沉补偿过程中不考虑钢丝绳活动端的任何收放运动,则滑轮包角变化将导致钢丝绳长度发生改变,即存在钢丝绳窜动现象。由式(4)可知,钢丝绳内绕时窜绳长度仅和α1、β1有关。

方案Ⅰ钢丝绳在A、B、C三个滑轮处的窜绳长度ΔLⅠ为

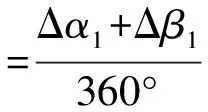
(7)

方案Ⅱ钢丝绳在A、B、C三个滑轮处的窜绳长度ΔLⅡ为

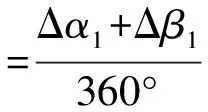
(8)

方案Ⅰ窜绳长度比方案Ⅱ的小12.4%。

此窜绳现象将导致浮动天车与游车之间的距离发生波动,假设天车升沉补偿系统采用的绳系为7×8,以方案Ⅱ为例,窜绳现象导致浮动天车和游车之间的距离波动为

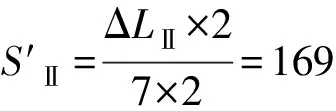
(9)

占总补偿行程7.62 m的2.23%,在一定程度上降低了天车升沉补偿系统的补偿精度和补偿效果。

3.1.4 直弯交变长度分析

钢丝绳在A、B、C三个滑轮处的包角变化除产生钢丝绳窜动现象以外,还导致部分钢丝绳一直处于拉直-弯曲交变状态。

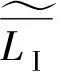
(10)

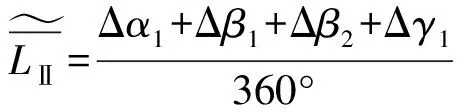
(11)

方案Ⅰ钢丝绳在A、B、C三个滑轮上处于拉直-弯曲交变状态下的长度比方案Ⅱ的大32.6%。

3.2 外绕式

3.2.1 数学建模

外绕式钢丝绳在A、B、C三个滑轮处的包角如图8所示,滑轮B处包角为α3,滑轮C处包角为β3,滑轮A处包角为γ3。

根据余弦定理可得

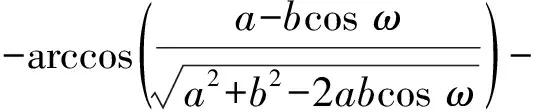
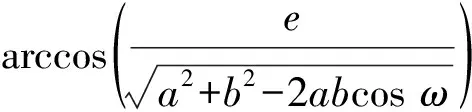
(12)

β3=180°-ω.

(13)

3.2.2 数值计算结果

建立式(12)、(13)的simulink程序框图,并将方案Ⅲ的各项参数输入到程序框图中,得到α3、β3随ω的变化趋势如图9所示。

图8 外绕式钢丝绳包角分析Fig.8 Wrappingangle analysis diagram of outer enwinding wirerope

图9 外绕式方案α3、β3随ω变化趋势Fig.9 Variation rules of α3 and β3 with ω in outer enwinding scheme

从图9可以看出:①α3随ω增大先迅速减小,当ω为95°时达到最小值,然后缓慢增大;②β3与ω互为补角,随ω增大线性减小。

结合式(3)和图9可得α3、β3随S的变化趋势如图10所示。由图10可以看出:①α3随S增大先迅速减小,然后减小趋势变缓,在S为5 500 mm时达到最小值,最后快速增大;②β3随S增大基本呈线性减小趋势。

图10 外绕式方案α3、β3随S变化趋势Fig.10 Variation rules of α3 and β3with S in outer enwinding scheme

3.2.3 窜绳长度分析

根据同位角定理可知,α3与α3′相等,γ3与γ3′相等,即总包角∑Gbj3为

(14)

即钢丝绳在A、B、C三个滑轮上的总包角恒定不变,因此外绕式钢丝绳不存在窜绳现象,不会对天车升沉补偿系统的控制精度带来不良影响。

3.2.4 直弯交变长度分析

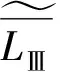
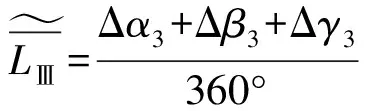
(15)

比方案Ⅱ的钢丝绳直弯交变长度小33%。

4 综合评价

基于线性加权和法进行综合评价。线性加权和法[18-20]计算公式为

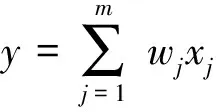
(16)

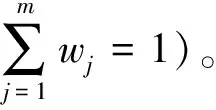
根据天车升沉补偿系统摇摆装置的功能要求,建立其评价指标为:成本影响、寿命影响和性能影响,采用层次分析法[21-22]确定三者的重要性比值为2∶3∶5。

权值的确定方法有很多,如主成分分析法、因子分析法、均差排序法等;采用经验法,通过邀请中海油研究总院的3名首席专家、中海油田服务有限公司5名现场专家各自独立地对各影响因素给出权重系数,并给出综合评价标准,最后平均得到天车升沉补偿系统摇摆装置的具体权重表如表2所示。

根据专家推荐值最终确定综合评价标准为:当y<1时,为优秀;当1≤y<2时,为良好;当2≤y<3时,为中等;当3≤y<4时,为较差;当y≥4时,为劣等。

将各影响因素数值分别代入式(16)可得3套天车升沉补偿系统摇摆装置的综合评价结果如表3所示。

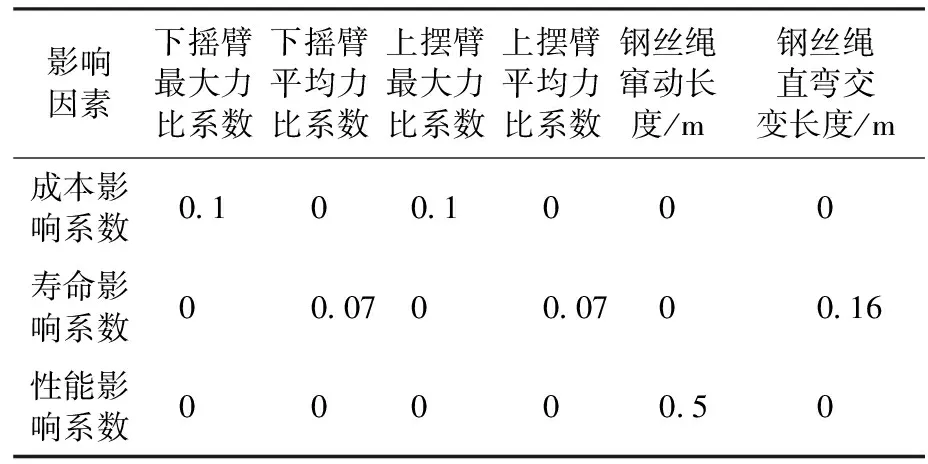
表2 基于线性加权和法的天车补偿系统摇摆装置权重Table 2 Weight of crown-block heave compensation system swing device based on onlinear weighted sum method

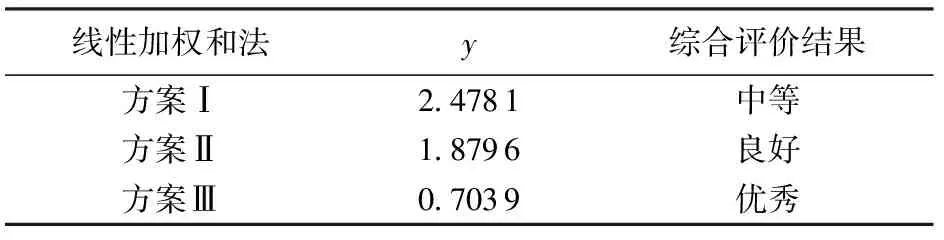
表3 三套方案的综合评价结果Table 3 Comprehensive evaluation results on three schemes

方案Ⅲ在摇摆臂受力工况、钢丝绳窜绳长度和直弯交变长度3个方面均优于方案Ⅰ和方案Ⅱ的,评价结果与分析数据结果相同。

5 结 论

(1)采用内绕式钢丝绳的两种方案摇摆臂受力变化规律及钢丝绳包角变化规律基本相近,但方案Ⅱ的摇摆臂受力及钢丝绳直弯交变情况优于方案Ⅰ,钢丝绳窜绳长度不如方案Ⅰ。

(2)与钢丝绳内绕式方案相比,钢丝绳外绕式方案具有摇摆臂受力基本恒定、无窜绳现象且钢丝绳直弯交变长度小等优点。

(3)基于线性加权和法建立的各影响因素的权重表和综合评价标准可作为天车升沉补偿系统摇摆装置工作性能评价的参考指标。