基于集对分析与三角模糊数耦合的水质评价模型
2018-12-10王文川李庆敏徐冬梅李文锦
王文川,李庆敏,徐冬梅,李文锦
(华北水利水电大学水利学院,河南 郑州 450046)
随着经济发展,水生态问题越发引起关注,全面了解、把握流域水质污染驱动因子是水生态治理中的基础性工作[1- 2]。从流域水污染驱动因子和水环境质量综合评价,展开水质污染科学问题的探讨研究,对构建符合我国河流特征的流域水生态治理体系,维护社会经济持续发展和流域生态环境安全具有重要的意义[3]。目前,水质评价的方法有很多,如:主成分分析法[4]、单因子污染指数法[5]、综合水质标识指数法[6]、模糊综合评价法[7]、灰色聚类法[8]等。众多学者从探讨影响水质的主要驱动因子和对和流水质等别划分等多个角度,进行水质评价方向的研究。如主成分分析通过将多个评价因子筛选出独立、不相关的综合因子,进而得到影响水质的主要驱动因子[9];模糊综合评价基于模糊理论考虑评价水质过程中的水质模糊性、复杂性和综合性,避免了不确定性的评价结果[10];单因子污染指数能较好的展现水质评价类别、功能区目标等信息。水质评价各有特点但在评价过程中也均有一定的局限性,如传统的模糊综合评价法利用最大隶属度原则来确定水质类别,但当各水质评价指标所属水质类别出现同步性较差时,往往难以建立有效的水质评价隶属度原则,使评价结果易出现差异度小、均化和间断等现象[11],传统的综合水质标识指数在指标权重分配上无法体现指标的差异性[12],集对分析可以较全面地描述水资源系统中的不确定性[13],该方法包容了模糊、灰色等不确定性判别方法的思想,通过用“同、异、反”三种状态对研究对象进行描述,并用联系数判别系统的归属程度。
水环境系统是一个典型的充满不确定性的大系统,其水质往往受多种因素影响,具有较大的波动性。在进行水质测量时,单一测量值往往难以体现出水质测量结果应具有波动性的特征。三角模糊数则适用于数据资料较少或难以精确测量的情况,该方法被广泛用于水质污染评价、水环境健康评价的研究中。本文将集对分析和三角模糊数结合,以区间的形式体现水质数据的波动性,利用三角模糊数和集对分析对竺山湾缓冲带湿地的水质构建评价模型,为水质的评价理论方法提供新的思路。
1 评价方法
1.1 集对分析
集对分析理论(set pair analysis)是我国学者赵克勤先生于1989年提出的一种不确定性系统分析新方法[14],见图1。

图1 集对分析模型示意图
集对是由一定联系的两个集合组成的基本单位,并用联系数将其表达为:
μ=a+bi+cj
(1)
式中,a,b,c—分别为集对分析理论中的同一性、差异性和对立性,当a,b,c∈[0,1],且a+b+c=1;i—差异度系数,取值范围:[-1,1];j—对立度系数,取值规定为-1。
由于在实际问题中,仅用三元联系数无法对问题进行好的描述,故在此基础上提出了多元联系数,将对象描述为同一、偏同差异、中差异、偏反差异和对立,其表达式为:
μ=a+b1i1+b2i2+b3i3+cj
(2)
式中,a,b1,b2,b3,c—联系分量,取值区间均为[0,1],且a+b1+b2+b3+c=1;i1,i2,i3—差异度系数;j—对立度系数。
本文所述的水质属于越小越优型,展开上述联系数表达式:
(3)
式中,m—第m个评价指标;n—第n个评价样本;s—评价指标样本值;s1~s5表示Ⅰ~Ⅴ级标准。
1.2 三角模糊数
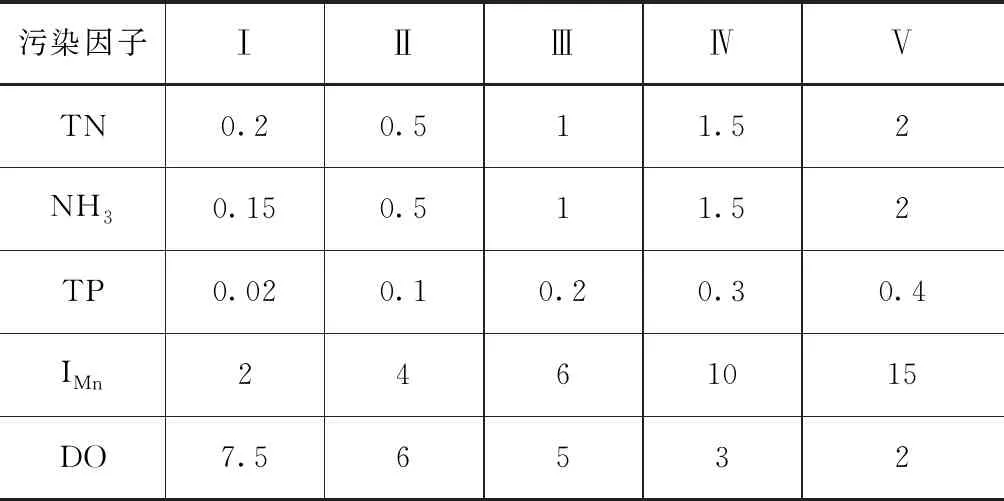
定义1[15]若a=(a1,a2,a3),其中,0 (4) 式中,μa—隶属度;x—某一变量。 将三角模糊数利用α截集进行数据简化处理。α为可信度,且α∈[0,1],数据区间由可信度水平决定,通常取α为0.9[16]。 (5) 集对分析式确定与不确定系统,其差异度的选取具有一定的模糊度,本文以三角模糊数(-0.5,0,0.5)为例,得到相应的差异度系数[17]。 (6) 式中,n取2,3,4,当s∈(s1,s3)时,η取2,当s∈(s3,s5)时,η取-2。 逐次计算求得矩阵数值的差异度系数后,结合设定的评价样本指标权重,可求得相应样本在设定置信区间内的综合联系数ym和等级值zm,计算公式如下[18]: (7) zm=3.5-2.5ym (8) 为验证集对分析与三角模糊数耦合模型的可行性与有效性,以文献[19]中的竺山湾水质实测数据为例进行计算。水质的评价与多项指标相关见表1,本研究将水质的分类选取溶氧量(DO)、高锰酸盐指数(IMn)、总氮含量(TN)、氨-氮(NH3)、总磷(TP)五项作为评价因子,参考地表水环境质量标准(GB 3838—2002),可将水环境质量评价标准分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ共五类。 表1 地表水环境质量划分标准限值单位:mg/L 对三角模糊数表示的水质区间数进行α截击处理,处理结果参照文献[19]。根据集对分析理论,构造水质评价联系数矩阵。竺山湾水质评价方案有m个评价指标(m=5),n个评价样本(n=13)。对 于区间形式,分别将和利用公式(6)算出差异度系数,差异度系数分为偏同差异度系数i1、中差异度系数i2、偏反差异度系数i3,将差异度系数代入公式(4),得出联系数矩阵,计算结果见表2。 集对分析与三角模糊数耦合方法的权重选取文献[19]中的权重,得到1×n的权重值矩阵w。 w=(0.1986 0.2046 0.2648 0.1980 0.1340) 表2 联系数表示的竺山湾缓冲带湿地水质数据 单位:mg/L 注:表中的数均是前面的大于后面的,这是由于公式6中需要加一个负号 表3 不同水质评价方法的竺山湾缓冲带湿地水质评价结果 将表2中的联系值结果和权重值矩阵根据公式(7)和(8)计算出相应的综合联系数和等级值。结果见表3。 根据集对分析与三角模糊数耦合模型计算的结果,对于采样点7,结合原始数据,总氮(TN)处于Ⅳ类,总磷(TP)、高锰酸盐(IMn)和溶氧量处于Ⅲ~Ⅳ类,结合目前对生态治理的重视,综合评定为Ⅳ级更为合理;采样点8、11、12三处污染严重,采样点8、12评定结果均为Ⅳ类,采样点11评定结果为Ⅴ类,这三处主要是由于总氮(TN)和总磷(TP)的含量过高导致;采样点3、4、5、6、7、13六处污染较为严重,评定结果均为Ⅲ类,这六处主要是由于总氮(TN)、总磷(TP)及高锰酸盐指数偏高导致的。总体分析,竺山湾水质处于污染状态,这与文献[16]和《太湖流域水资源公报2013》的结果基本一致。 从与综合水质标识指数法及模糊标识指数法的对比发现,集对分析与三角模糊数耦合的结果与综合水质标识指数法的评价结果较接近。 模糊标识指数法结合了改进的模糊层次分析法和综合水质标识法的优点,不仅给出水质级别和水功能区达标程度,同时克服了不能评定劣Ⅴ类水质的缺点[20],但从评价的结果发现,采样点8、11和12虽然总磷(TP)和总氮(TN)的含量偏高,但其余三个评价因子的含量处于Ⅱ~Ⅳ级,故该方法对于竺山湾湿地带的评价结果偏高。 综合水质标识指数法,该方法可以完整表达水体总体的综合水质信息,结合定性、定量进行水质评价,对个别水质监测数据有较好的降噪性,能得出较为合理的水质评定结果[21]。结合原数据分析,发现评价结果合理,准确性较高。 本文方法利用集对分析,重视水质评价问题的不确定性,结合相应的权重强化了各监测点主要污染因子的作用,得出的结果相对可靠,但对于单个评价因子存在重度污染是,对综合评价的影响结果不足,可能到能评价结果偏低,需要做出相应的改进。 竺山湾水质评定结果分布在Ⅱ~Ⅴ类,未能符合当地的水质要求,其中总氮、总磷、高锰酸盐指数污染较为严重。因此,对于后期竺山湾水环境的治理应重点削减氮、磷、高锰酸盐有机污染物。

1.3 差异度系数
1.4 评价模型
2 实例应用


3 讨论与结论
