基于波速度比较的多分支配电架空线故障定位方法
2018-12-10朱建刚宋晓东张国栋马永明
朱建刚,陈 平 ,宋晓东 ,张国栋 ,马永明
(1.国网山东省电力公司滨州供电公司,山东 滨州 256610;2.山东理工大学 电气与电子工程学院,山东 淄博 255049;3.国网山东省电力公司高青县供电公司,山东 淄博 256300;4.国网山东省电力公司高密市供电公司,山东 潍坊 261500;5.国网山东省电力公司微山县供电公司,山东 济宁 277600)
0 引言
10 kV配电架空线网架结构复杂,分支数目较多[1-2],故障时折反射波的数次叠加导致传统的行波定位测距方法适用困难。另外,小电流接地方式下单相接地故障电流较小,故障特征不明显,使现有多种接地故障定位方法失效。多分支结构的配电线路同时具有以上两个故障定位难点,必须予以重点关注,设法化解或避开定位阻碍。
文献[2-3]提出改进行波法,优化了二次行波波头的识别方法,但在实际配电线路结构中适用性较差。文献[4-5]提高了信号注入法抗干扰能力,但线路网络复杂的情况下,可能存在信号检测困难、定位效率偏低的问题。文献[6]提供了基于双端行波信息的配电网故障定位方法,但局限于单相接地故障,不能应对相间短路故障。文献[7-10]考虑多端故障信息,基于时差关系进行故障定位,为本文开展配电线路故障定位研究起到了一定的启发作用。
分析多分支配电架空线路拓扑结构,建立树枝状线路结构模型,基于典型架空线T型线路结构,研究故障初测速度与实际波速度间大小关系所指示的故障区段特征,提出基于波速度比较的架空线故障选段方法,并依靠双端测距原理准确锁定故障位置。依照故障选段—故障点两阶段定位思路,整理形成一套针对多分支配电线路故障的综合定位方法。
1 多分支配电架空线路结构简化
常见的配电架空线路多采用典型树枝状分支结构,主干线路作为从变电站10 kV出线母线引出的直连线路,沿途线路往往设置分支线路,每一条分支线路均通过分界开关引出。随着电力用户增加,配电网络辐射扩增,为满足实际负荷增加的需要,在分支线路上往往又引出了下一级分支,即子分支线路,每一条子分支线路多以线路末端配变终断。
因不能穷尽所有支路情况,故分析架空线结构需要对复杂分支网络作简化等效。图1给出了典型架空线路树枝状拓扑结构,图中架空主干线用线路lPQ表示,两端点用P、Q表示。分支线路lMA、lNB分别经分支点M、N引出,支路lMA上含有两条子分支线路lM1A1和lM2A2,分别经子分支点 M1和M2引出,同样支路lN1B1和lN2B2是支路lNB上两条子分支线路,分别经子分支点 N1和 N2引出。 A、B、A1、A2、B1、B2分别表示各支路末端。将各支路末端设置为行波检测点,并假设故障初始行波到达各检测点的时间为tα(α=A、B、A1、A2、B1、B2)。

图1 典型架空线路树枝状拓扑结构
2 基于波速度比较的配电架空线路故障定位
2.1 T型配电线路故障分支判定
选择T型线路作为分析对象,如图2所示。其中O为T型线路的分支节点,LXO、LYO和LWO分别表示3条分支臂的长度,不妨设定故障发生在lOY段,故障点f到分支点O的距离是x。
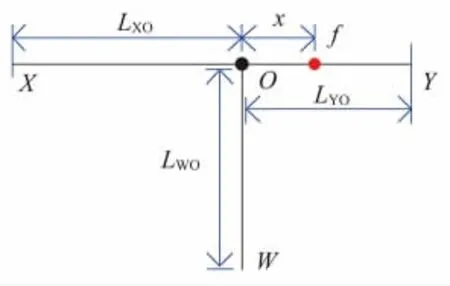
图2 T型线路
为便于分析,在此提出故障初测速度的概念:T型线路内连接分支点O的两条分支臂的长度之和与对应两测量端初始行波到达时间之和的比值。对照图2的线路,故障初测速度用公式表示为:

式中:tX1、tY1和tW1为 f点故障后,故障初始行波传播至端点X、Y和W的所用时间,可通过对线路分界、分段开关动作和多级继电保护的时间配合分析,依靠馈线自动化进行信息整理获取。分析行波传输过程,求得行波经过线路X-O-Y、X-O-W和Y-O-W的实际波速度,并与故障初测速度对比如下:

由式(4)~(6)发现,若求取故障初测速度的两个T型线路分支臂均不包含故障点,则求得的线路初测速度小于线路的实际波速度;若故障初测速度对应的两分支臂中有任何一个发生故障,那么求得的线路初测速度就等于实际线路波速度。因此利用比较各区段的故障初测速度与实际波速度的大小关系可实现对故障区段进行确定,并形成以下判据:
1)由式(4)可知区段 lXO或 lYO有故障,由式(6)可知区段lYO或lWO有故障,取两者的公共部分,则判定lYO段为故障区段;
2)亦可直接由式(5)知线路中区段lXO和lWO无故障,故也可判定故障位于区段lYO;
3)特殊情况下,若故障位置趋近于点分支点O,则线路3个初测速度均近似等于实际波速度,此时就判定故障点处在T型线路的分支节点处。
2.2 树枝状配电线路故障分支的判定
配电网线路多采用树枝状分支结构,无法直接运用T型配电线路故障分支的判定方法,因此对于类似图1这样含子分支的架空线路段,应对其繁琐的树枝状结构做一定的简化,等效为多个简单的T型结构线路的组合,这样T型线路故障区段的判定思路便可同样得到运用。
如图3为一段多分支结构架空线,各线路区段名称用小写字母编号标明,含有m个分支节点,分别用 jk(k∈{1,2,…,m})来表示,有 n 个末端,分别用 ei(i∈{1,2,…,n})来表示,故障点 f 位置如图 3所示。末端测得故障初始行波到达的时间记为tei( i∈{1,2,…,n})。
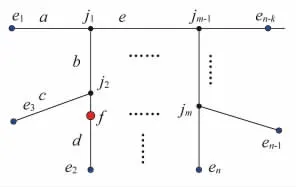
图3 多分支架空线路结构
在已知线路拓扑结构和各区段长度的前提下,获取任意线路分支点与末端之间的距离,记为djkei。例如dj1e2表示分支点j1与末端e2间的距离。这样就构建了n×m阶的行波传播距离矩阵,用D表示:

对于由区段a+b、c和d构成的T型线路,求取T型线路中各区段的故障初测速度及其与线路实际波速度的大小关系为:

由式(8)可知线路中区段a或b或区段d有故障,由式(10)可知线路中区段c或区段d有故障,取两者的公共区段,则判定d段为故障区段;亦可以直接通过式(9)知线路中区段a、b和区段c无故障发生,故也可判定故障位于区段d,即节点j3与末端e2之间。
当故障发生在其他分支线路上和分支节点处时,分析过程与上述故障发生位置分析一致,分析思路不变。
2.3 故障点的确定
利用双端测距原理,选用末端e1和e2作为测量端,得到故障点 f与末端e2的距离为
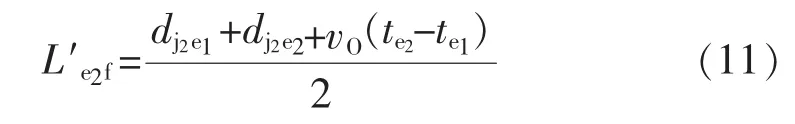
再选择末端e3和e2作为测量端,得故障点 f与末端e2的距离为

取两距离的平均值作为故障点f到末端e2的距离。
3 仿真验证
3.1 仿真模型建立及参数设置
按照图4线路结构,在PSCAD环境下搭建线路仿真模型。各段线路用小写字母表示,长度见表1。

图4 10 kV配电线路网络

表1 各段线路长度 km
仿真采样频率选择10 MHz,架空线采用3 Conductor Delta Tower模型,模型中10 kV架空线选用钢芯铝绞线JKLGYJ-240/40,直径为21.66 mm,直流电阻为0.120 9 Ω/km。为减小波速度对定位准确度的影响,采取如下处理以减小波速度偏差:
1)在已知线路模型基础上,将多个线路末端设为故障行波检测点,在某一已知固定点处设置故障,获取故障后初始行波到达不同端点的所用时间;
2)利用时间与距离关系,一一求取某一端点对应的波速度;
3)将以上波速度取平均值作为该固定故障点对应的实际波速度;
4)再设置另外不同的故障点,重复1)~3)过程,将多个故障点对应的波速度取平均值,作为该线路最终的行波传播速度。
经多次实验和计算,得出行波在架空线中的传播速度为 2.75×105km/s。
求取该线路行波传播距离矩阵D为

式中:矩阵元素单位为km。
3.2 仿真验证分析
设架空分支线lM1A段f2点在t=0时刻发生A相金属性接地短路,故障点f2到支路末端A的距离为1.5 km。架空线路各末端及线缆连接点所测得的故障电流波形与对应模极大值如图5~7所示,各分支末端初始行波到达绝对时间如表2所示。

图5 P端与Q端故障电流与对应模极大值
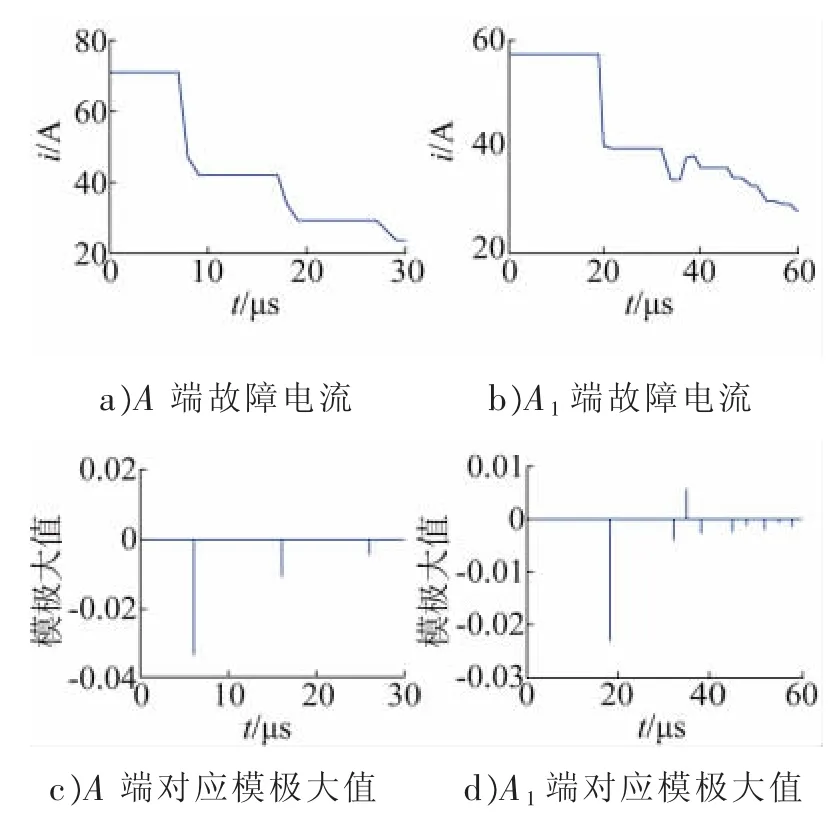
图6 A端与A1端故障电流与对应模极大值
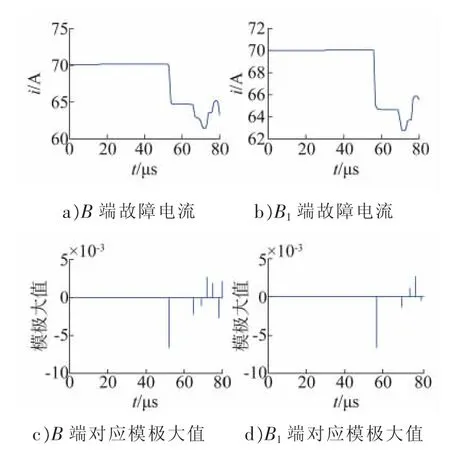
图7 B端与B1端故障电流与对应模极大值

表2 f1点故障各端点初始行波到达时间 μs
对于线段lPM1、lM1A和lM1A1构成的T型线路,求取T型线路中各区段的量测波速度及与线路实际波速度的大小关系为:

由式(14)可知线路区段lMM1或lM1A有故障,由式(16)可知线路区段lM1A1或lM1A有故障,取两者公共部分,则判定lM1A段为故障区段;亦可由式(15)知区段lMM1和lM1A1无故障发生,故也可判定故障位于区段lM1A。
先选用P端和末端A点的行波测量时间,进行双端测距,得到故障点f2距离支路末端A的距离为

再选用末端A1和末端A点的行波测量时间,测量距离为

取两距离的平均值作f2到末端A的距离,即1.512 5 km,误差为12.5 m。表3给出了架空线不同位置故障时的测距结果。
由表3可知,对于不同故障位置,特别是分支点附近的故障点,运用基于波速度比较的故障定位方法均可清晰判定故障区段,并确定故障位置。观察仿真数据,定位误差保证在150 m以内,满足实际线路小于200 m的理论误差要求。
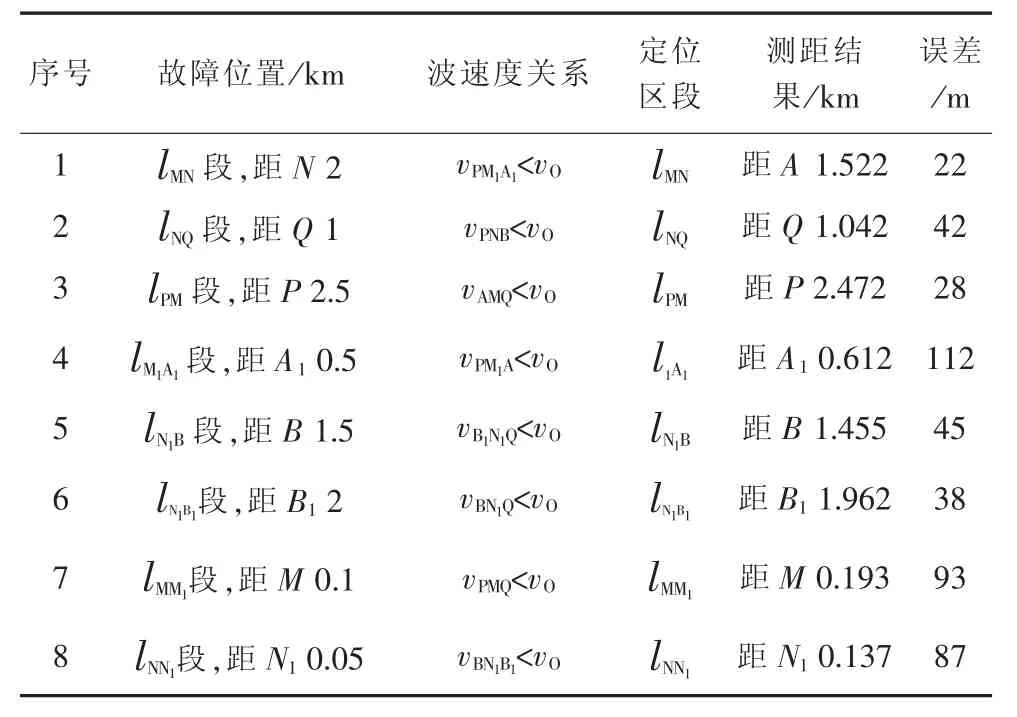
表3 架空线故障定位结果
4 结语
提出的基于波速度比较的架空线故障综合定位方法,具有较高的故障定位精度和可靠性,从波速度大小关系上获取故障信息,定位逻辑清晰;针对多分支结构的架空线路,可应对分支结构更复杂的线路故障;需要比较多端间的行波信息,受到行波采集设备性能和时钟同步精度的影响。
