高频扰动下的双馈风机系统频率响应及其振荡风险分析

吴 雨，薛安成，付潇宇，王子哲

（1.国网江苏省电力有限公司无锡供电公司，江苏 无锡 214000；2.新能源电力系统国家重点实验室（华北电力大学），北京 102206）

0 引言

近年来，随着新能源发电装机容量的逐年攀升，大量的电力电子设备接入电力系统，使得电网运行特性和控制特性变得非常复杂[1]，由此产生了一系列新的振荡问题，其中，发生在直流外送系统中的中高频段振荡问题尤其受到学者关注。文献[2]分析了德国北海风电场发生的250～350 Hz高频振荡现象。文献[3-5]提及舟山五端直流输电工程的中高频分量（以二次谐波为主）导致跳闸的事件。文献[6]分析了鲁西直流工程发生的1.2 kHz左右高频振荡现象。文献[7]针对高压直流系统中发生的高频振荡，提出采用特征根法来分析系统等效参数、稳态运行点等关键因素对振荡的影响，从而为振荡的抑制提供理论依据。

另一方面，大规模新能源经直流外送是当前趋势之一，因此，双馈/直驱风机等主要的新能源发电设备可能会感受到来自外送系统的高频扰动，并响应放大，形成振荡问题。然而，值得注意的是，对于外界周期扰动的响应，现有研究主要集中在次同步频率扰动下的响应传播机理问题[8-11]，如文献[8]分析并推导了次同步振荡电流在MMCHVDC（基于模块化多电平换流器的高压直流输电）系统中的分布及传播机制；文献[9]详细推导并分析了转子绕组中的单个频率扰动电压在定子绕组中感应出单个主要频率的响应电流的频率和幅值；文献[10]、文献[11]分别分析了次同步振荡电流在永磁直驱风机系统和双馈风机各环节的传播与响应机理。而对于高频扰动下的双馈/直驱风机系统响应问题目前鲜有报道。

此外，对于双馈风机的阻抗频率特性分析主要集中在次同步段，而对高频段很少关注。如文献[12-14]基于双馈风机的阻抗特性分析了双馈风机-串补系统的次同步振荡机理及其影响因素。

对此，本文研究了高频扰动下双馈风机系统的多频率响应，并对其振荡风险进行了初步分析。首先，基于高频扰动信号的响应路径，定性推导并分析了受控异步机系统/网侧换流器系统各环节的频率响应，获得了受控异步机系统/网侧换流器注入系统的各频率响应，揭示了整个双馈风机系统在并网点输出受高频扰动下的电流多频率响应。进而通过扫频法和阻抗法分析了200～1 100 Hz高频段内双馈风机系统的阻抗频率特性，验证了基于简化模型的阻抗法的有效性，并初步评估了双馈风机系统高频振荡风险。

1 双馈风机系统多频率响应分析

1.1 响应机理分析

根据文献[11]的推导和定义，双馈风机系统分为受控异步机系统（含转子侧换流器）和网侧换流器系统。

当并网点存在频率为fp的高频扰动信号时：

（1）受控异步机系统（运行在工频f1下，转速频率为fm）最终在转子侧绕组中产生频率为fp-fm，fp-2f1+fm，2fp-f1-fm，2fp-3f1+fm的电压和电流扰动分量，其中fp-2f1+fm分量幅值大于2fp-f1-fm和2fp-3f1+fm分量幅值；在定子侧绕组中会产生fp，fp-2f1，2fp-f1，2fp-3f1频率的电流扰动分量并注入并网点，其中fp-2f1分量幅值大于2fp-f1和2fp-3f1分量幅值。如表1所示。

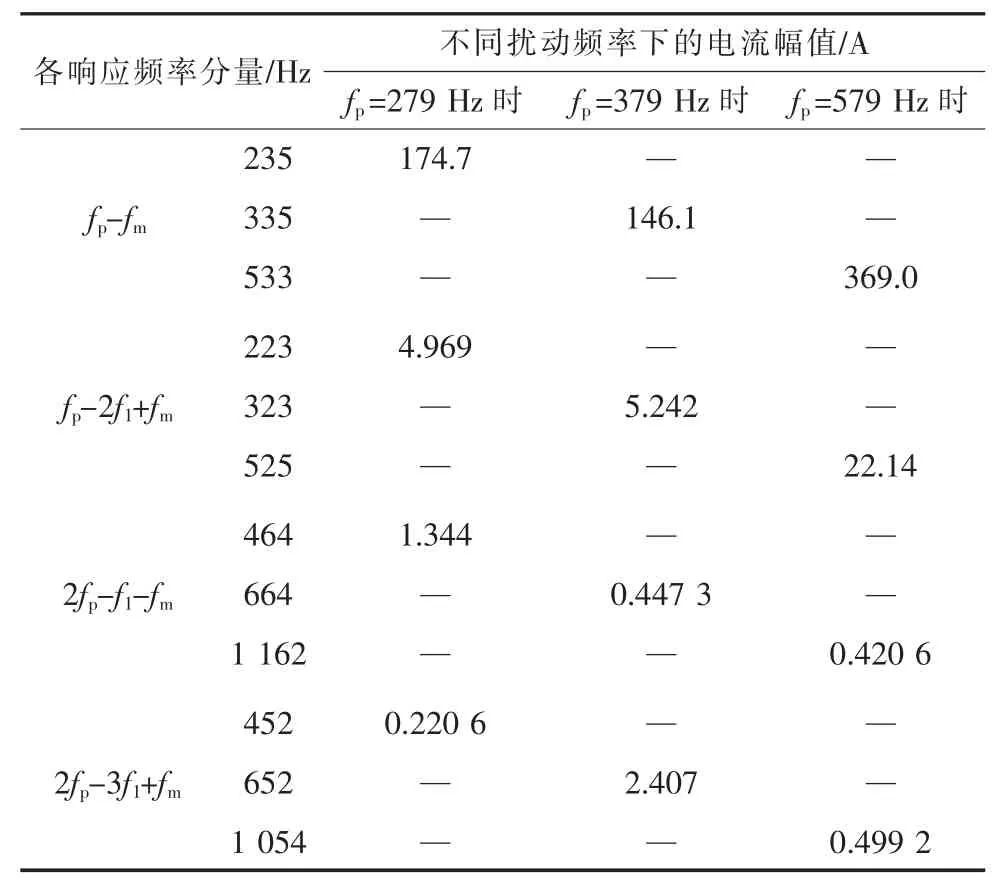
表1 转子a相电流的频率响应

（2）网侧换流器系统会向并网点输出频率为fp， fp-2f1， 2fp-f1， 2fp-3f1的电流扰动分量。

（3）整个双馈风机系统会向并网点输出频率为fp，fp-2f1，2fp-f1和2fp-3f1的电流扰动分量。

1.2 仿真验证

在PSCAD中搭建了并网双馈风机系统模型，仿真分析不同频率高频扰动下的系统频率特性。扰动频率fp分别设置为 279 Hz，379 Hz和579 Hz，转子转速频率fm分别设置为44 Hz和46 Hz。

不同频率的高频扰动下，转子a相电流各主要频率响应分量的幅值如表2所示，其中279 Hz扰动下转子a相电流的对数幅频特性如图1所示。

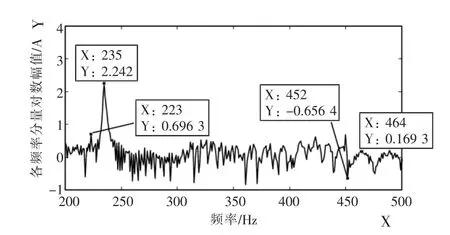
图1 转子a相电流的频谱特性

图1表明，当系统存在频率为279 Hz的高频扰动时，转子a相电流存在235 Hz（fp-fm），223 Hz（fp-2f1+fm）， 464 Hz（2fp-f1-fm）， 452 Hz（2fp-3f1+fm）的频率分量。其中，235 Hz为主要的响应频率分量；223 Hz分量幅值比平常的噪声大，较明显；而464 Hz和452 Hz分量含量较小，淹没在噪声中。同时，结合表1可知，转子a相电流的2fpf1-fm和2fp-3f1+fm分量幅值明显小于fp-2f1+fm分量幅值，与理论分析结果一致。

图2—4分别为受控异步机子系统、网侧换流器子系统和双馈风机系统输出电流的对数幅频特性，三者均包含 179 Hz（fp），279 Hz（fp-2f1），508 Hz（2fp-f1）， 408 Hz（2fp-3f1）的频率响应， 这与理论分析结果一致。其中，定子a相电流的179 Hz分量幅值比平常的噪声大，较明显；而408 Hz和508 Hz的频率分量量级很小，淹没在噪声里；网侧换流器和并网点a相总电流的各分量幅值均比平常的噪声大，较明显。

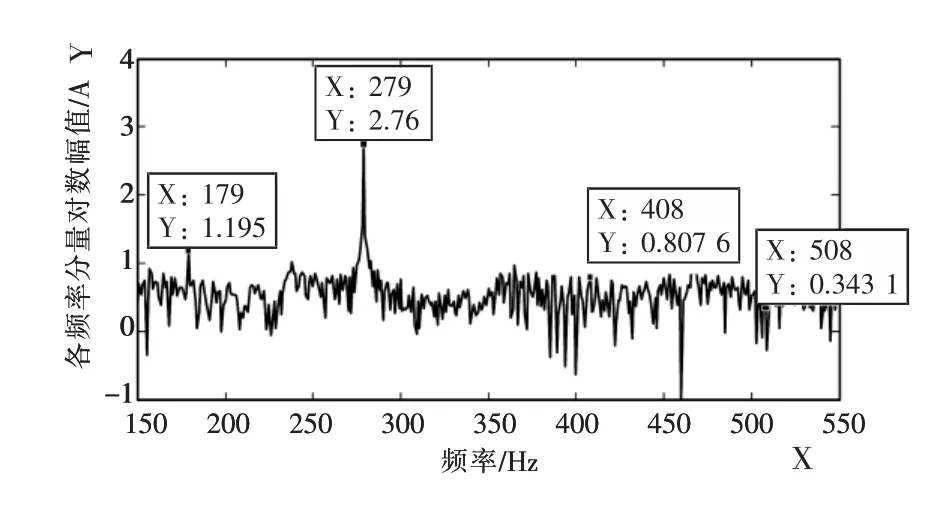
图2 定子a相电流的频谱特性

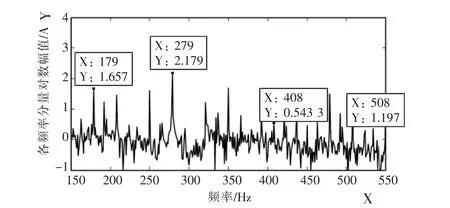
图3 换流器出口a相电流的频谱特性

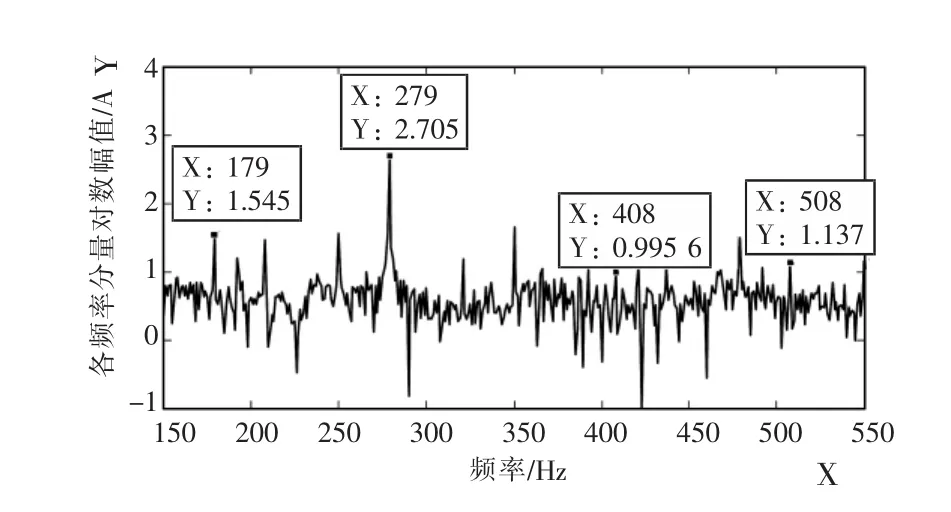
图4 并网点a相总电流的频谱特性

同时，结合表2可知，三者输出电流的2fpf1，2fp-3f1分量幅值均小于fp-2f1分量幅值，这也与理论分析结果一致。

此外，双馈风机向并网点输出的电流多频率响应主要来自于网侧环流器系统，且扰动频率越高，网侧换流器系统产生的响应比重越大。

2 双馈风机系统高频振荡风险分析

由前文分析可知，双馈系统在高频下对应的输出稳定与否，决定了系统是否会发生高频振荡。目前，设备阻抗频率特性分析是判断系统振荡风险的常用方法，因此，为实现快速评估振荡风险，本节建立了双馈风机的简化阻抗模型，并与扫频法所得阻抗进行对比，以验证理论模型的准确性。之后基于该简化模型可实现双馈风机在高频段振荡风险的初步评估。

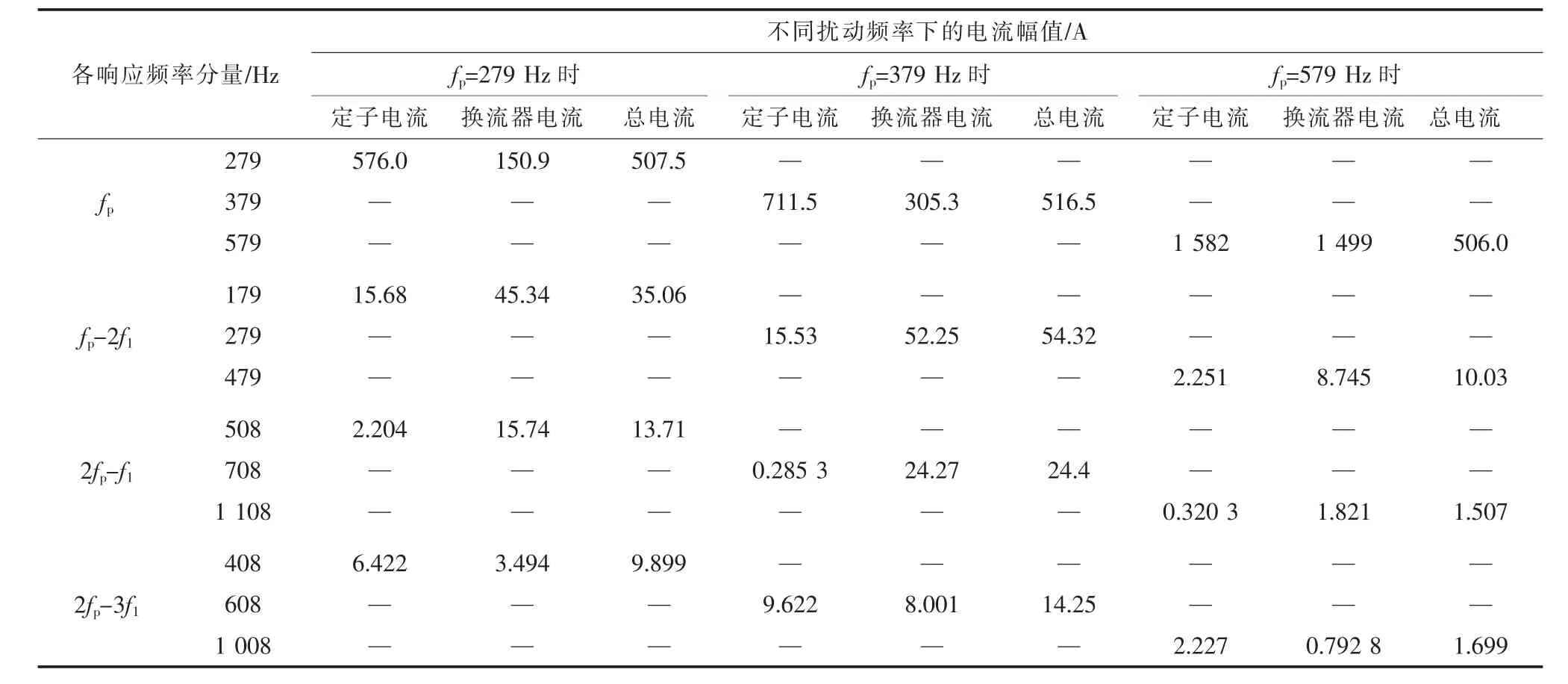
表2 双馈风机系统输出的电流频率响应

2.1 双馈风机系统阻抗建模

双馈风机阻抗（ZDFIG）由受控异步机系统阻抗（ZCAMS）和网侧换流器系统阻抗（ZGSCS）并联构成，如式（1）所示。

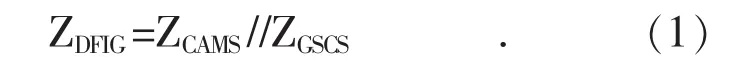
2.1.1 受控异步机系统阻抗模型

对于受控异步机阻抗，采用文献[12]中的简化阻抗模型，即不考虑RSC（转子侧换流器）的外环控制以及锁相环的动态过程，如式（2）所示：

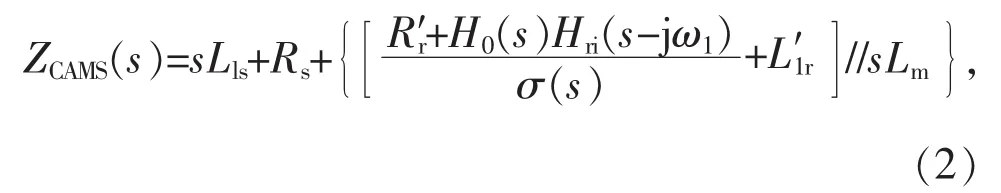
式中：Rs，Lls分别为定子绕组电阻和漏抗电感；Lm为感应电机的励磁电抗电感；分别为折合到定子侧的转子绕组电阻和漏抗电感；ω1为振荡角频率， ω1=2πf1， f1为振荡频率； σ（s）为转差率；Hri（s-jω1）为 RSC 电流内环的传递函数； H0（s）为RSC换流器指令值到出口值的传递函数。

其中：

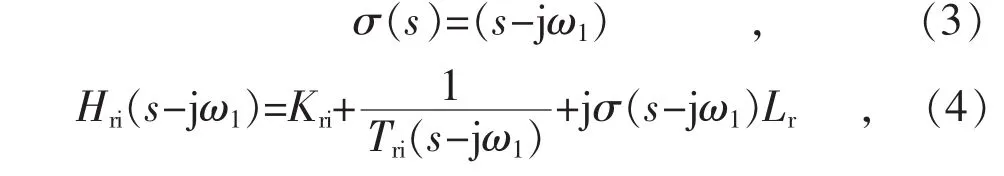
式中：Kri，Tri分别为双馈风机RSC电流内环的比例参数和积分参数； σ（s-jω1）Lr为 RSC 电流内环dq轴控制解耦项系数。

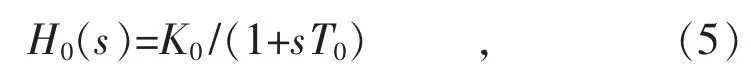
式中：K0，T0分别为一阶滞后环节的比例参数和时间常数。

2.1.2 网侧换流器系统阻抗模型

网侧换流器系统阻抗（ZGSCS）由GSC（网侧换流器）阻抗（ZGSC）和滤波器阻抗构成，类似于受控异步机系统，其阻抗模型如式（6）所示：

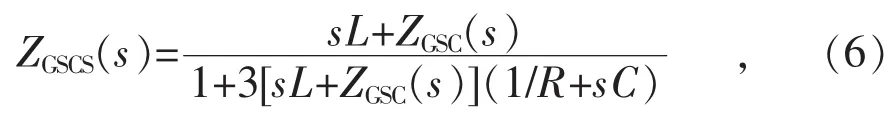
式中：R，L，C分别为网侧换流器出口滤波器中的电阻、电感、电容。

滤波器结构如图5所示。

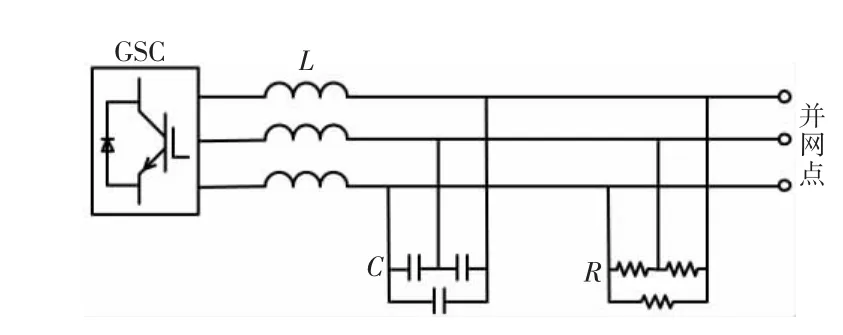
图5 GSC出口滤波器示意

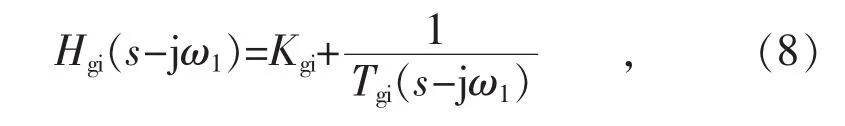
式中：Kgi，Tgi分别为双馈风机转子侧换流器电流内环的比例参数和积分参数。

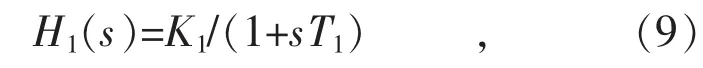
式中：K1，T1分别为一阶滞后环节的比例参数和时间常数。

2.2 振荡风险分析

根据式（1）、 式（2）、 式（6）确定的双馈风机阻抗模型，计算并绘制出受控异步机系统、网侧换流器系统以及整个双馈风机的阻抗频率特性，并与扫频法所得结果进行比较，见图6。

网侧换流器阻抗如式（7）所示：

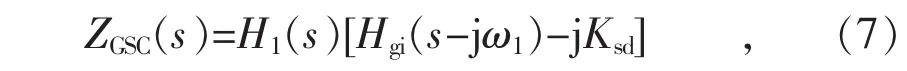
式中：Ksd为GSC电流内环dq轴控制解耦项系数；Hgi（s-jω1）为 RSC 电流内环 PI（比例-积分）环节的传递函数；H1（s）为RSC换流器指令值到出口值的传递函数。

其中：

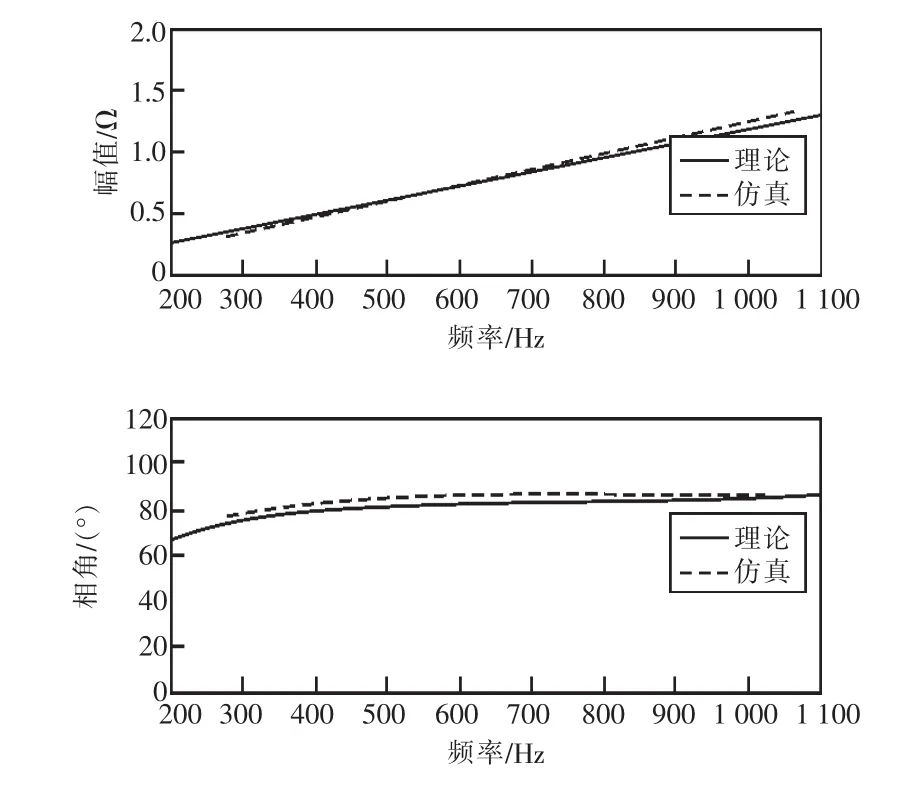
图6 受控异步机系统阻抗频率特性

2.2.1 受控异步机系统阻抗频率特性分析

表3表明，理论计算阻抗与仿真所测阻抗的误差在1 000 Hz附近较大，这是由于受控异步机系统在高频段其结构和参数发生明显的改变，如存在较多的杂散电容，而建模过程中未考虑这些因素，但总的来说，最大误差在7%内，因此上述频段内受控异步机系统阻抗模型具有较高的准确性。

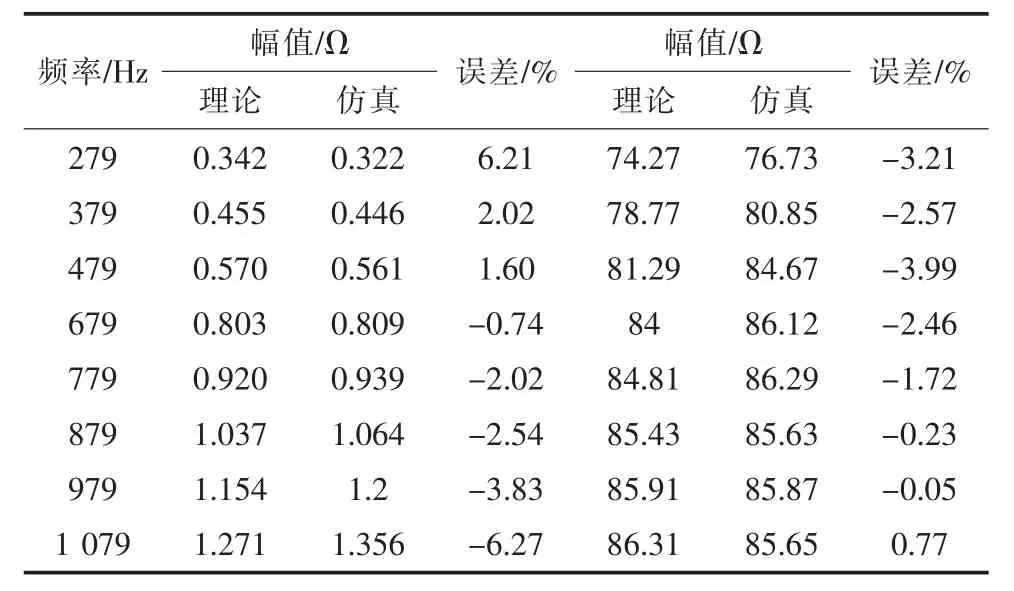
表3 受控异步机系统阻抗

同时，结合图6可知，在200～1 100 Hz频段内，受控异步机系统阻抗呈现正电阻-电感性质，且随着频率的增大，受控异步机系统阻抗模值近似线性增大。

2.2.2 网侧换流器阻抗频率特性分析

图7和表4为网侧换流器系统的理论计算和扫频法所得阻抗频率特性对比。表4表明，在200～400 Hz和 800～1 100 Hz范围内阻抗模值的理论计算结果与仿真结果误差在10%内，相角的误差也在12%以内；而在400～800 Hz频段内阻抗模值误差最大可达27.92%，因此，网侧换流器系统阻抗模型在200～400 Hz和800～1 100 Hz频段内的有较高的准确性，而在400～800 Hz频段内则误差较大。该误差是由于忽略锁相环引起的，具体而言，本文中锁相环的带宽在400～800 Hz的范围内，因此在该频段内对网侧换流器模型具有较大影响。

同时，结合图7和表4可知，在200～1 100 Hz频段内，网侧换流器系统阻抗呈现正电阻-电容性质，且随着频率的增大，网侧换流器系统阻抗模值减小。

2.2.3 双馈风机系统阻抗频率特性分析

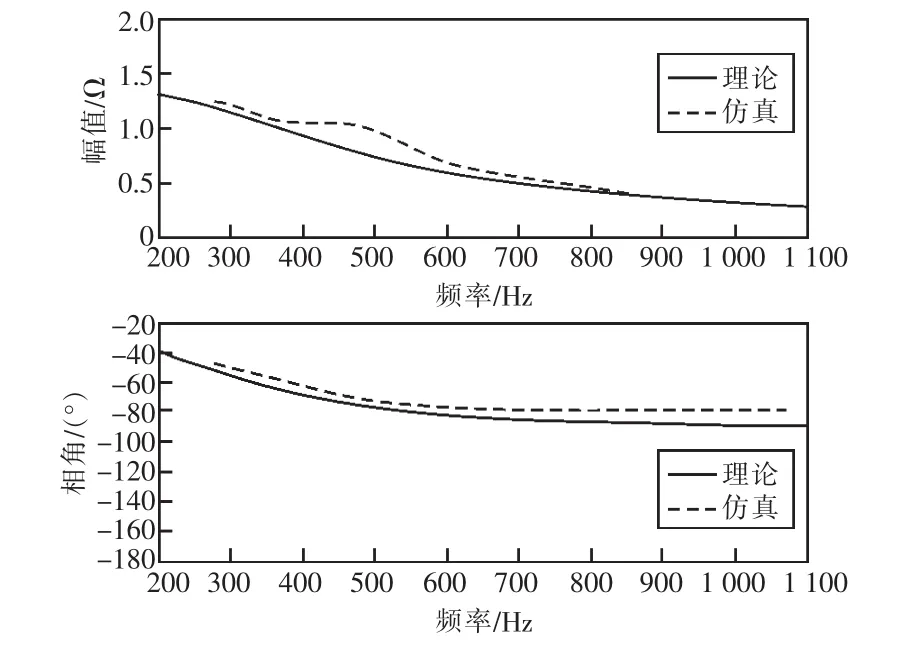
图7 网侧换流器系统阻抗频率特性

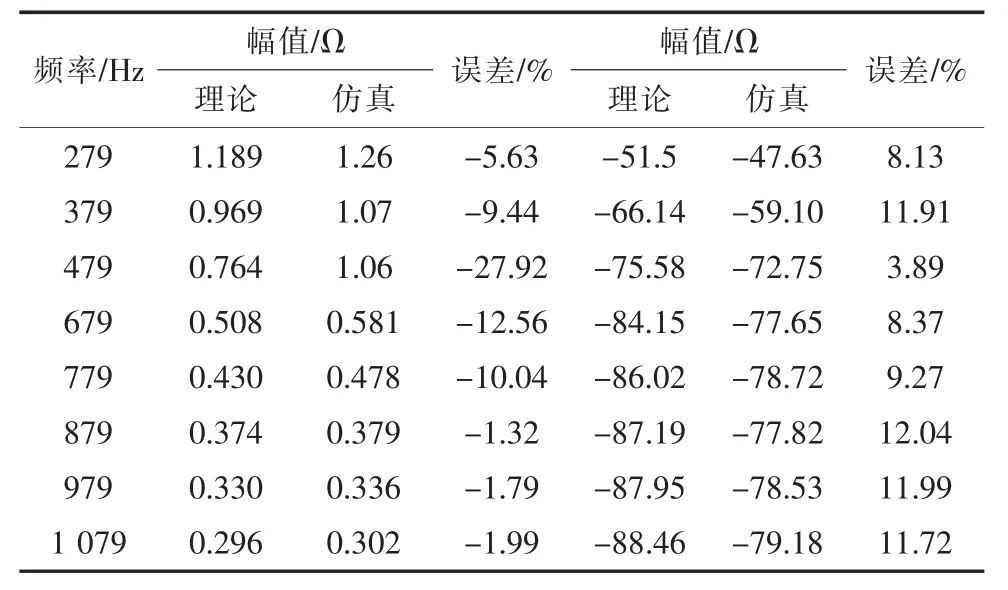
表4 网侧换流器系统阻抗

图8 双馈风机系统阻抗频率特性

图8和表5分别为双馈风机系统的理论计算和扫频法所得阻抗频率特性对比。表5表明，在200～400 Hz和 800～1 100 Hz范围内阻抗模值的理论计算结果与仿真结果误差在10%内，相角误差在20%内；而在400～800 Hz频段内阻抗的相角误差最大接近40%。

具体而言，双馈风机系统总阻抗的误差取决于阻抗小的子系统的误差。在200～400 Hz频段内，受控异步机系统阻抗模值明显小于网侧换流器系统阻抗，而其在该频段误差较小，因此系统总阻抗误差较小；在400～800 Hz频段内，网侧换流器系统阻抗接近或小于受控异步机系统，而其在该频段误差较大，因此系统总阻抗误差较大；在800～1 100 Hz频段内，网侧换流器系统阻抗明显小于受控异步机系统，而其在该频段误差较小，因此系统总阻抗误差较小。

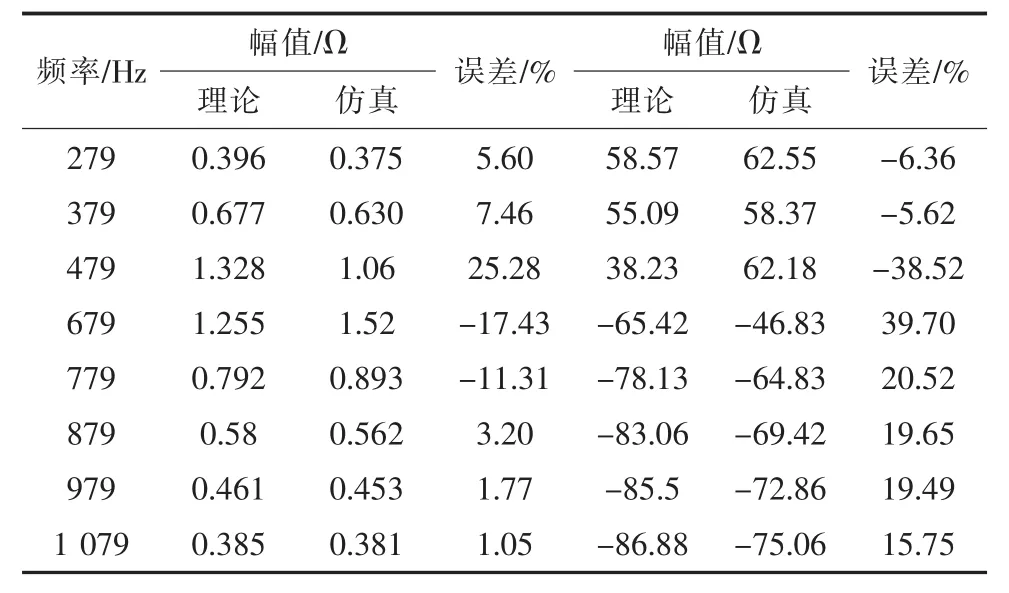
表5 双馈风机系统阻抗

结合图8和表5可知，在200～500 Hz频段内，双馈风机系统阻抗呈现正电阻-电抗性质（该频段受控异步机系统阻抗模值较小）；在500～1 100 Hz频段内呈现正电阻-电容性质（该频段网侧换流器阻抗模值较小），且随着频率的增大，网侧换流器系统阻抗模值先增大后减小。

综上所述，本文研究的双馈风机阻抗模型在200～400 Hz和 800～1 100 Hz频段内有较高的准确性，在400～800 Hz频段内理论模型准确性相对较低。目前可利用该阻抗模型实现双馈风机系统在部分频段振荡风险的初步筛选和排查，未来需建立更加详细的模型（考虑锁相环、控制外环等）来实现对更多频段振荡风险的研究。

从振荡风险的角度看，本例在900～1 100 Hz频段双馈风机系统呈现电容性质，可能与呈现电感性质的外电网构成等效谐振回路；同时，该频段的双馈风机阻抗角接近-90°且阻抗模值相对较小，即呈现弱阻尼性质，因此，在900～1 100 Hz频段双馈风机外送系统有一定的振荡风险。

3 结论

本文基于传递函数的思想分析了高频（大于200 Hz）扰动下双馈风机系统的多频率响应，并通过阻抗法和扫频法分析了高频段双馈风机的振荡风险。结论如下：

（1）当并网点存在频率为fp的高频扰动信号时，类似于次同步扰动，双馈风机系统会向并网点输出多个频率为n1fp-n2f1的电流频率响应，其中，fp和fp-2f1分量为主要的频率响应分量，2fpf1和2fp-3f1分量幅值较小。

（2）双馈风机系统向并网点输出的电流频率响应主要为来自网侧换流器系统输出的电流频率响应。

（3）本文所建立的双馈风机阻抗模型可对部分频段的振荡风险进行初步筛选和排查，未来需建立更加详细的模型来实现对其他频段振荡风险的研究。