课间学生更换教室耗时分析及教室排课方案优化设计

诸葛雪玉

(河海大学土木与交通学院，江苏 南京 210098)

1 概述

目前，国内外关于排课问题主要从两个角度着手研究：教学管理工作者从方便教学管理的角度出发，大多依据经验确定教室排课方案[1]；计算机专业从优化求解算法[2]、提高运算效率角度出发来确定排课方案，研究成果丰富。但是大家都忽略了交通对排课系统的影响，缺乏针对排课方案中学生通行时间、通行效率等指标的量化分析与评价。

据此，借助交通工程学、运筹学等相关理论，分析并量化课间学生更换教室途中各阶段时间消耗，以人均时耗最短为优化目标，优化教务管理系统中的排课方案，对提高课间利用率和减缓课间拥堵有一定的意义。

2 课间学生更换教室行程时间建模

通过分析学生课间更换教室过程中排队进出教室、路径通行、排队打水、排队如厕等阶段，研究各阶段消耗时间的影响因素。其中排队进出教室考虑学生早到因素的影响；路径通行分别考虑路径选择与路径拥堵两个因素；课间排队打水与如厕阶段分别考虑学生打水、如厕的使用时间、排队时间以及到达分布等因素的影响。

2.1 进出教室的时间消耗

在考虑学生早到因素影响下，构建学生排队进出教室消耗时间模型，则有：

(1)

其中，tE为一个教室学生排队进出教室消耗的总时间；VE为学生排队进出教室速率；t′为一个教室因学生早到造成的拥堵延误时间；n′为等待班级的上课人数。

2.2 路径通行的时间消耗

在路径通行阶段下，通过分析路径选择与路径拥堵[3]等影响因素，构建考虑多需求的路径通行时间计算模型。在无拥堵条件下，借助最短路原则[3]确定更换教室路径选择。构建无拥堵条件下的路径通行时间计算模型，其计算公式为：

(2)

其中，tL为一个教室学生课间更换教室通行路径消耗总时间；DE为更换教室时直接到达终点教室的路径长；VB为直达终点教室路段的通行速率；n为上课教室总人数。

在拥堵条件下利用图解法，计算路径中瓶颈点处拥堵增加的通行时间，则有：

(3)

其中，tt为拥堵点所增加的时间；k为拥堵点上游人流率；u为拥堵点能够通过的最大人流率。

学生更换教室途中，排队进出教室消耗的时间和路径通行消耗的时间t1为：

t1=∑tE+∑tL+∑tt

(4)

2.3 打水过程的时间消耗

打水过程时间消耗包括排队打水时间消耗及因打水需求而产生的额外的路径时间消耗。排队打水消耗时间借助排队论[4,5]方法进行研究，打水过程中学生到达服从泊松分布，打水时间服从负指数分布，打水过程类似排队论的多路多通道服务，即N个M/M/1系统。构建打水过程的时间消耗模型，计算公式为：

(5)

2.4 如厕过程的时间消耗

如厕过程时间消耗包括排队如厕时间消耗及因如厕产生的路径时间消耗。如厕排队消耗时间借助排队论方法研究，如厕过程中学生到达服从泊松分布，如厕的时间服从负指数分布，如厕过程类似排队论的单路多通道服务，即M/M/N系统。构建如厕过程的时间消耗模型，计算公式为：

(6)

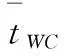
则学生课间更换教室的途中，因打水和如厕消耗的总时间t2为：

(7)

其中，Δt为课间时长；m为课间排队打水学生所占的比例；p为课间排队如厕学生所占比例。

2.5 总计行程时间

(8)

3 排课系统优化设计

3.1 优化目标及约束条件

在考虑各阶段耗时因素的影响下，以课间学生更换教室人均耗时最短为优化目标。总结现状排课规律加以优化对整个学期的课程重新进行安排，在此基础上对教室安排方案进行约束。约束条件包括教室上课人数不大于教室容量，具有特殊需求班级在对应的特色功能教室上课，将有学生早到行为的班级安排在行人流上游，以及将连续授课教师授课教室固定。构建数学模型如下：

(9)

其中，C为教室容量；c′为有特殊需求班级集合，或第一节课没课班级集合；R′为特殊功能教室集合，或行人流上游教室集合；T为连续授课教师集合；R为教室集合;R1为第一节课的上课教室;R2为第二节课的上课教室;式中映射均为一一映射。

3.2 优化算法

根据教学培养方案确定每个班级每个学期每门课程的上课时长，借助现有排课规律加以优化，构建班级与课程之间的联系，形成初始排课方案。

根据教室间距离、教室容量和班级人数、课程等数据，利用贪心算法[6]求得初始排课方案(确定初始解)，根据可行解搜索求得新的解，若新的排课方案学生课间更换教室人均消耗时间更短，则将新的解置为当前最优解。重复迭代过程，当搜索次数或迭代次数大于规定阈值时，停止迭代并输出当前解作为最优排课方案。利用优化算法求解时遵从相关优化原则：在保证安全的前提下尽量降低学生课间更换教室频率，尽量减少在拥堵点附近教室安排学生上课，尽量使学生在更换教室路径中途经过厕所与打水处。

4 实例验证

4.1 现状分析

以河海大学江宁校区为例，研究其2017年—2018年学期在江宁校区致用、致高A、致高B、博学四栋教学楼，以16级，17级本科生5 152人作为研究对象的课间耗时情况，其中包括上课教室146个、厕所43个、饮水机31个。在此基础上将江宁校区教室及教学服务设施抽象为立体空间网络：其中教室、饮水机、厕所抽象为网络节点，通行路径抽象为网络节点间的联通路径，据此计算学生更换教室路径通行的距离。

4.2 模型验证

选择五个教室内的班级为实测研究对象。记录第六周周二上午课间各个教室学生进出教室时间，两个时间之差即为各学生在更换教室途中消耗时间。将现场实测的人均耗时与根据模型计算所得人均耗时进行对比，可知实测结果与模型计算结果差异比例近似，且变化趋势基本一致，这表明构建的课间学生更换教室行程耗时模型可信度较高，具体如图1所示。

4.3 优化分析

以第六周周二上午为例，根据现状分析确定各个参数的数值，计算各阶段的时间消耗，按照前述优化目标、优化原则进行优化，确定优化后教室排课方案，并对比分析现状与优化排课方案的学生更换教室通行时间消耗(如表1所示)。

表1 河海大学江宁校区教室排课方案优化前后学生课间通行时耗分析

计算可得，排课方案优化前后学生课间更换教室人均耗时分别为9.8 min和6.7 min，通行时耗降低31.6%，原教室数为114个，优化教室数为72个，且优化方案在更换教室过程各阶段均降低通行时间。

5 结语

从交通角度优化排课系统，可以有效提高课间时间的利用效率，为优化课间休息时长提供科学依据。同时，通过量化学生打水、如厕过程的时间消耗，可进一步优化饮水机等教学服务设施的布设位置与数量。