竞争环境下轴–辐式海运网络设计与定价决策

赵宇哲周晶淼迟国泰

(1.大连海事大学交通运输管理学院,辽宁大连116026;2.大连理工大学管理与经济学部,辽宁大连116023)

1 引 言

以枢纽港口为中心的轴–辐式海运网络是迈向海运一体化进程中出现的一种能够适应全球海运系统的网络形态,这一拓扑结构可利用枢纽港口之间的规模经济效应为海运企业在满足托运人海运需求的基础上显著降低其运营成本.然而,轴–辐式海运网络的建设中港口投资大、可变因素多[1],设计决策的失误往往会给海运企业带来巨大的经济损失.另一方面,海运企业在海运市场上能否具有话语权,关键在于提供的海运服务是不是唯一的,特别在海运服务的同质性正不断趋强的今天,其定价决策是决定托运人选择的根本因素[2].当前,我国正大力扶植海运业,鼓励本国的海运企业参与国际竞争.全球海运业的领导者——马士基已在欧亚、亚美航线上完成了轴–辐式海运网络的建设,产生的规模经济效应使其具有一定的行业定价权,而对于正努力开拓全球海运市场的中远海等我国一些海运企业而言,如何结合定价决策来设计符合其自身优势的轴–辐式海运网络以争取更多的市场机会,具有重要的现实意义.

轴–辐式海运网络设计对于海运企业而言是一个战略决策,其本质在于不同情境下的枢纽选址问题在海运上的应用[3,4].直接相关的具有竞争性的枢纽选址问题研究中,Marianov等[5]第一个针对市场上领导者与跟随者的竞争问题建立了枢纽选址模型,提出了跟随者若想进入市场需通过设计新的枢纽和降价的方式.Gelareh等[6]考虑了价格/时间等因素,建立了一个可用于评估跟随者该如何进入市场的枢纽选址模型.赵宇哲[7]在Gelareh等[6]研究的基础上,建立了基于吸引力函数的枢纽选址模型,研究结果表明若领导者决策不能与跟随者同步,其市场份额将会受到威胁.但是,上述枢纽选址模型均是离散的,即选址的枢纽节点数量是给定的,忽视了枢纽节点确定的内生性问题.枢纽选址问题在海运上的应用研究中,赵宇哲等[8]综合考虑了起讫港口之间的流量大小与规模经济效应的关系,基于弧–流量的变量建立了IMO海运CO2排放体系下可确定枢纽港口选址和干线支线上港口挂靠次序的枢纽选址模型.Zheng等[9,10]针对沿海运输权规制、海运服务创新等因素对海运网络设计的影响,基于路径–流量的变量建立了不同目标权衡下关于航线设计的枢纽选址模型.上述枢纽选址模型均结合其研究需要来建立的,由于海运服务的吸引力是本文关键的考量因素,于是在忽略不同港口之间的流量大小前提下可采用固定的规模经济效应,同时应选择基于路径–流量的变量,因其比基于弧–流量的变量更易分解.除此之外,上述研究还证实了枢纽港口选址和基于枢纽港口的航线连接是轴–辐式海运网络设计的根本决策[11].值得注意的是,轴–辐式海运网络设计虽为海运服务奠定了基础,但海运企业之间的竞争关键仍在于谁提供的海运服务对托运人更具吸引力,可见定价决策对于海运企业而言是一个战术决策.关于吸引力的研究可追溯于Reilly[12]提出的确定性模型,Eiselt等[13]延伸了Reilly吸引力模型的思想,将综合了价格/时间/质量的比例模型运用至具有竞争性的枢纽选址问题中.不过,相比确定性模型,离散选择模型能更好的解释(服务的)吸引力与托运人选择行为之间的关系.因此,如何将关于托运人选择行为的定价决策与轴–辐式海运网络设计相联系是一个难点[14].至于枢纽选址问题的求解,大多枢纽选址问题为0-1/混合0-1规划问题,连续化方法可凭借连续松弛、连续等价将其转化为连续问题求解,具有很高的实用价值[15].但是,该方法仍处于研究早期阶段,所提到的大部分方法只对线性规划问题适用,不具备通用性,于是可用于求解非线性规划问题的连续化方法仍有待进一步开发.

鉴于上述分析,本文将结合不同海运企业在海运市场上的地位,分别建立领导者以成本导向与跟随者以需求导向的轴–辐式海运网络设计与定价决策模型.对于跟随者而言,通过轴–辐式海运网络设计这一战略决策促使其实现利润最大化,但反之,获取利润又取决于战术决策–定价决策是否具有吸引力.针对二者建立的离散枢纽选址模型与连续枢纽选址模型,分别利用CPLEX与Lambert W函数、NCP函数、凝聚函数和增广Lagrange乘子罚函数法对线性0-1规划问题与非线性混合0-1规划问题进行求解;最后,对不同情境下跟随者的轴–辐式海运网络设计与定价决策进行算例仿真,以验证模型和算法的有效性.

2 问题描述

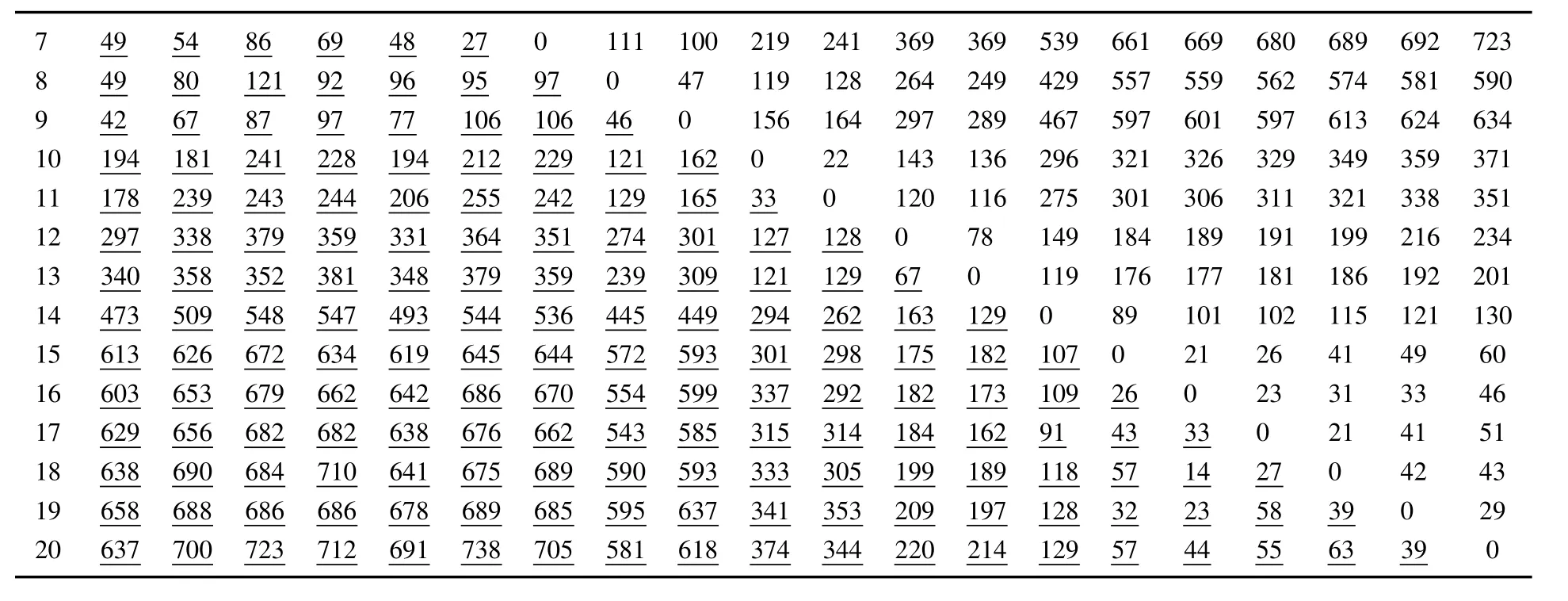
假设某海运市场由领导者A运营,其设计的轴–辐式海运网络GA=(N,VA)中,港口集合N=HA∪SA,HA为枢纽港口集合,SA为非枢纽港口集合;航线集合VA={(i,s,t,j)|i,j∈N,s,t∈HA},i为起点港口,j为讫点港口.GA=(N,VA)设计周期一般是3个月～6个月,每年须调整至少两次[16].在固定有限的周期内,Qij(j≠i)表示海运市场上非弹性的需求量,即起讫港口i,j之间的OD流量表示任一港口u为枢纽港口的投资(租赁)成本;规模经济效应α∈(0,1]表示枢纽港口s,t之间运输的折扣因子.GA=(N,VA)是领导者A在满足所有OD流量的基础上,依据成本最小化原则设计pA个枢纽港口完全连接的轴–辐式海运网络.领导者A的定价策略是成本导向的成本加成,即单位运输成本上加上固定百分比Δ的利润来确定其单位运输价格因此,领导者A需解决的问题在于:1)最优的枢纽港口选址hAs;2)基于枢纽港口s,t的航线连接VA.

一个计划进入同一海运市场的跟随者B,在与领导者A统一的决策周期内,通过设计符合自身优势的轴–辐式海运网络GB=(N,VB),以需求导向的定价策略来捕捉某些航线上的市场机会.其中,港口集合N=HB∪SB,航线集合VB={(i,k,l,j)|i,j∈N,k,l∈HB},起讫港口i,j之间的OD流量Qij,投资成本规模经济效应α,单位运输成本与领导者A设计GA=(N,VA)时类同.但是,GB=(N,VB)是跟随者B依据利润最大化原则设计的,跟随者B获取的利润为在固定有限的周期内捕捉到的OD流量带来的总收入减去总运输成本与总投资成本,其在设计GB=(N,VB)时不与领导者A共享枢纽港口,但可取相同港口作为枢纽港口.因此,跟随者B需解决的问题在于:1)枢纽港口数量pB和最优的枢纽港口选址hBk;2)基于枢纽港口k,l的航线连接VB;3)最优定价决策(单位运输价格);4)若其单位运输成本比领导者A高,可否获取利润.

大多轴–辐式海运网络设计研究确立了起讫港口i,j之间的航线连接上(枢纽)港口的挂靠次数[7-9].假设领导者A与跟随者B提供的航线连接VA,VB上枢纽港口的挂靠次数不大于2.以跟随者B为例,航线连接VB有两个港口的航线连接(i,j)∈HB×HB∪HB×SB∪SB×HB,三个港口的航线连接(i,k,j)∈SB×HB×HB∪SB×HB×SB∪HB×HB×SB和四个港口的航线连接(i,k,l,j)∈SB×HB×HB×SB.一般地,起讫港口i,j之间的航线连接是唯一的,须在上述航线连接中选择其一[7-9].

托运人在起讫港口i,j之间选择领导者A与跟随者B提供的航线连接VA,VB时主要对比为其提供的单位运输价格鉴于Logit模型已在运输领域的一些著作中被充分验证[17],运用Logit模型来表示托运人关于定价决策的离散选择,其中灵敏度参数Θ表示托运人对单位运输价格的敏感程度,即Θ值越高表示托运人对单位运输价格越敏感,越倾向于选择更经济的航线连接;反之,托运人会选择其它航线连接.

3 轴–辐式海运网络设计与定价决策模型

为简化问题,提出基本假设:

1)轴–辐式海运网络的结构相对稳定,不考虑灾害、战争等突发状况对海运网络设计的影响;

2)轴–辐式海运网络中所有OD流量,海运企业在任意两个港口u,v∈N之间的单位运输成本和已知且固定,不考虑运力限制;

3)轴–辐式海运网络中枢纽港口由海运企业投资(租赁),不考虑枢纽港口的中转成本;

4)轴–辐式海运网络中枢纽港口的容量足够容纳所有OD流量,不考虑因枢纽港口容量限制而由其它航线连接的分摊问题.

模型1领导者A成本最小化的轴–辐式海运网络设计模型如下

式(1)为领导者A在固定有限的周期内轴–辐式海运网络设计的成本最小化,包括总运输成本与总投资成本.式(2)为领导者A决定设计枢纽港口的数量约束;式(3)表示起讫港口i,j之间有且仅有一条航线连接;式(4)和式(5)表示起讫港口i,j之间的航线连接上经过的必须是枢纽港口,不能在非枢纽港口中转,且不允许超过两个枢纽港口;式(6)表示起讫港口i,j间的航线连接的单位运输成本;式(7)表示领导者A的决策变量为0-1示性变量.

模型2跟随者B利润最大化的轴–辐式海运网络设计与定价决策模型为

式(8)为跟随者B在固定有限的周期内轴–辐式海运网络设计的利润最大化.式(9)表示起讫港口i,j之间的OD流量同时经过跟随者B与领导者A的枢纽港口,由二者以竞争方式共同分担.式(10)和式(11)为跟随者B与领导者A对于托运人在起讫港口i,j之间的OD流量的吸引力函数,即托运人在对比二者在起讫港口i,j之间的单位运输价格基于Logit模型来离散选择二者的OD流量比例;式(12)表示领导者A成本加成的定价策略;式(12)～式(16)与模型1的约束式(3)～式(6)类同;式(17)表示跟随者B决策变量的可行域.

4 模型求解

模型1和模型2可独立求解,模型1的结果(枢纽港口s,t∈HA)需作为模型2的输入变量.其中模型1是一个离散枢纽选址模型,是线性0-1规划问题,可通过CPLEX直接求解;模型2是一个连续枢纽选址模型,是非线性混合0-1规划问题.对于模型2,基于Lambert W函数推导可得的最优定价决策将其转化为非线性0-1规划问题,再利用连续化方法NCP函数、凝聚函数和增广Lagrange乘子罚函数法进行求解.

4.1 最优定价决策

定理1任一起讫港口i,j之间的航线连接(i,k,l,j)的最优定价决策为

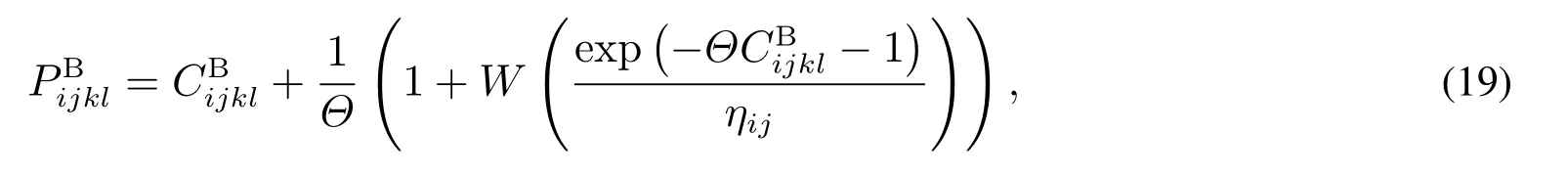
其中W(·)是Lambert W函数,即为f(w)=wexp(w)的反函数.

证明式(18)可分解为每一起讫港口i,j之间可独立表达的航线连接,于是对任一起迄港口i,j之间的航线连接,存在某一特定k,l∈N有

对所有的k,l,根据式(20),任一起迄港口i,j之间的航线连接有

4.2 基于NCP函数的连续问题

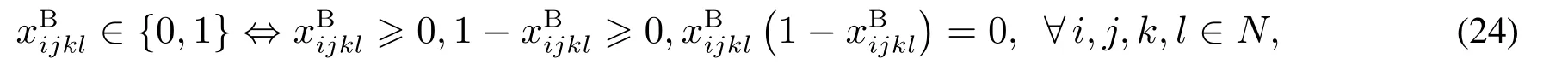
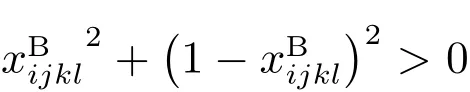
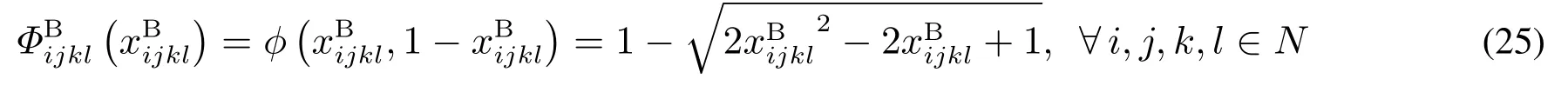
是可微的,式(25)的梯度为

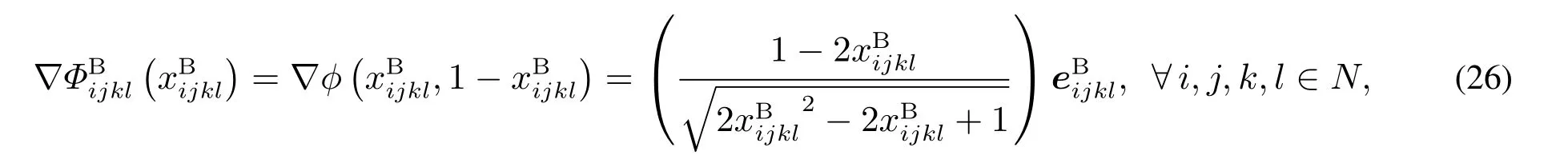
进一步有

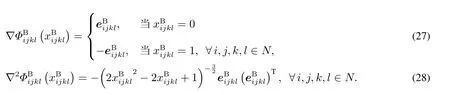
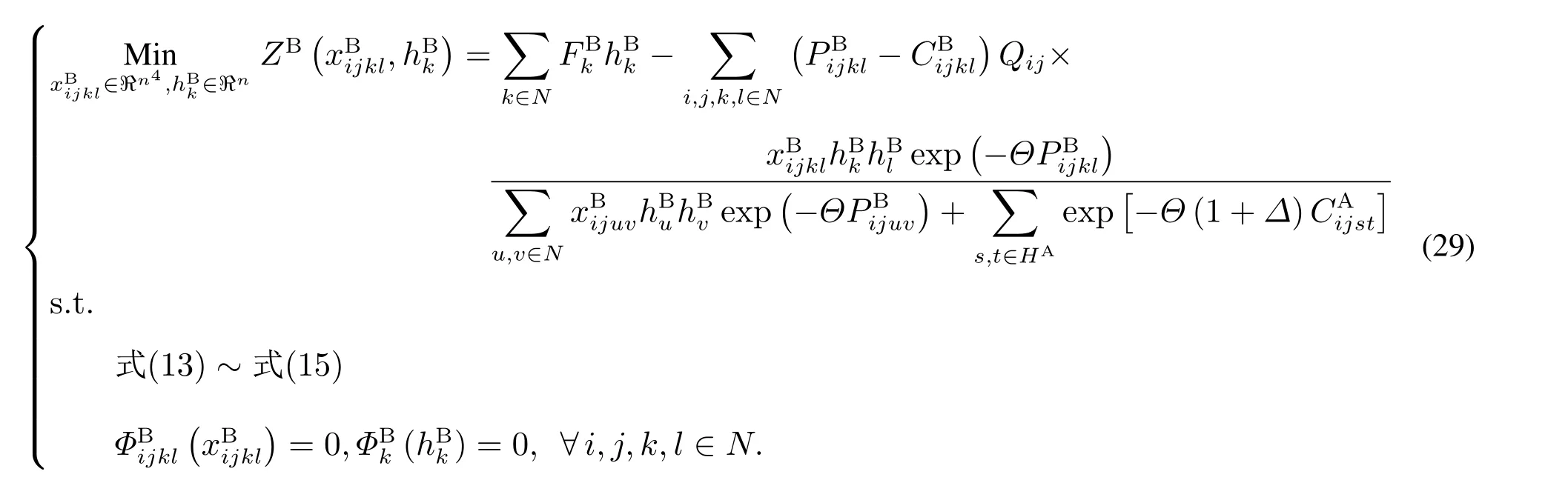
4.3 基于凝聚函数的松弛问题

对于问题(29),采用乘子罚函数求解时,需引入(n4+2n3+n2+n)个Lagrange乘子,增加了乘子迭代的难度.

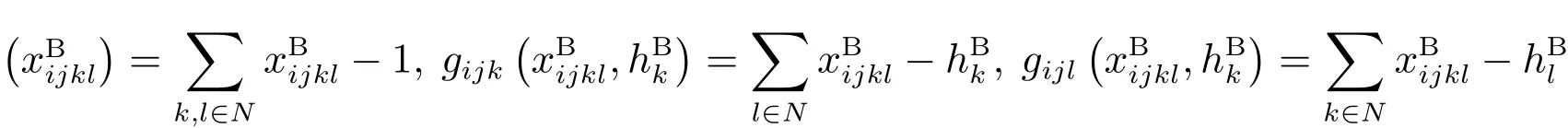
其中ε为凝聚参数.

对于问题(35),引入Lagrange乘子λ1和罚因子σ1,求得增广Lagrange松弛问题

4.4 基于增广Lagrange乘子罚函数的算法

取

为下次迭代的Lagrange乘子.基于增广Lagrange函数的算法可写成

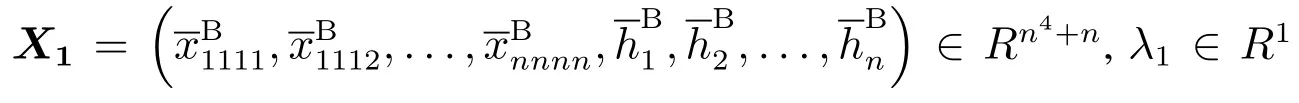
步骤2求解问题(37),给出若∥ψε(Xκ+1)∥≤δ,或κ=K,则停;

步骤 3若∥ψε(Xκ+1)∥2≤∥ψε(Xκ)∥2/4,则转步骤 4;σκ←10σκ,转步骤 2;

步骤4计算λκ+1;σκ+1← σκ,κ ←κ+1,转步骤2.

5 算例仿真

5.1 数据选取

假设存在一个港口集合Γ={1,2,...,20}的海运市场,在固定有限的周期(6个月)内,所有起讫港口i,j之间非弹性的需求量Qij(OD流量)服从均匀分布∪[252,5692](TEU).领导者A与跟随者B选择任一港口u为枢纽港口的投资(租赁)成本FAu和FBu服从均匀分布∪[19 800,101 200](USD),二者在任意两个港口u,v∈Γ之间的单位运输成本列于表1.计算时,枢纽港口之间运输的折扣因子α={0.2,0.4,0.6,0.8,1},领导者A决定设计枢纽港口的数量pA={1,2,3}与其定价的成本加成Δ={0.1,0.3,0.5,0.7,0.9},托运人对单位运输价格的灵敏度参数Θ={0.001,0.004,0.007,0.010,0.013},通过CPLEX对领导者A成本最小化的轴–辐式海运网络设计模型进行求解,领导者A的枢纽港口选址s,t∈HA与成本ZA结果列于表2.

表1 领导者A与跟随者B的单位运输成本C和C(带下划线),单位:USD/TEUTable 1 Unit transportation costs Cand Cof the leader A and the follower B(underlined),unit:USD/TEU

表1 领导者A与跟随者B的单位运输成本C和C(带下划线),单位:USD/TEUTable 1 Unit transportation costs Cand Cof the leader A and the follower B(underlined),unit:USD/TEU

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 0 46 52 55 48 70 68 56 47 179 189 315 321 489 612 617 621 637 648 651 2 64 0 21 22 31 51 52 89 81 201 231 354 367 512 634 641 644 671 681 690 3 15 0 21 41 69 71 104 97 224 241 364 371 541 661 667 669 684 694 709 4 43 39 0 37 61 67 103 95 221 237 361 369 539 654 669 671 690 681 716 5 62 25 37 0 44 49 81 77 198 221 349 361 501 621 634 634 661 671 681 6 68 19 26 53 32 74 61 46 0 11 110 102 224 236 367 370 541 659 671 679 691 689 721

续表1Table 1(continue)

表2 领导者A的枢纽港口选址s,t∈HA与成本ZATable 2 Hub ports s,t∈HAand total cost ZAof the leader A

5.2 算法结果与验证

跟随者B的轴–辐式海运网络设计与定价决策问题中,港口集合Γ={1,2,...,20},是一个大规模的算例,直接利用现有算法和优化软件求解是不可能的.因此,通过与可寻找问题的较好可行解的遗传算法对比,以验证所设计模型算法的适用范围与求解性能.取Δ=0.5,Θ=0.004,pA=2,α={0.2,0.4,0.6,0.8,1}与Δ=0.5,Θ=0.004,α=0.4,pA={1,3};因基于Lambert W函数推导可得的最优定价决策是独立的,将计算结果(四维矩阵)代入模型2中.对于所设计模型算法,ε=10-6,X1=(0.5,0.5...,0.5),λ1=1,σ1=104,δ=10-2,K=300;对于遗传算法,种群规模=200,适应度函数采用轮盘赌算法,交叉概率=0.9,变异概率=0.1,终止进化代数=1 000,此时其收敛速度近似终止.利用Matlab R2013a编程运行,将所设计模型算法与遗传算法的计算结果列于表3,其中Obj列表示两种方法获得的目标函数值Obj1,Obj2;Time列表示所设计模型算法的运行时间;Dev列表示所设计模型算法与遗传算法的目标函数值的偏差程度,即100(Obj1-Obj2)/Obj2.

表3 所设计模型算法与遗传算法的计算结果对比Table 3 A comparison of computational results for the desined algorithm and genetic algorithm

5.3 仿真结果与分析

图1 不同规模经济效应α对跟随者B利润ZB的影响Fig.1 The influence of different economics of scale(α)on profits of follower B(ZB)

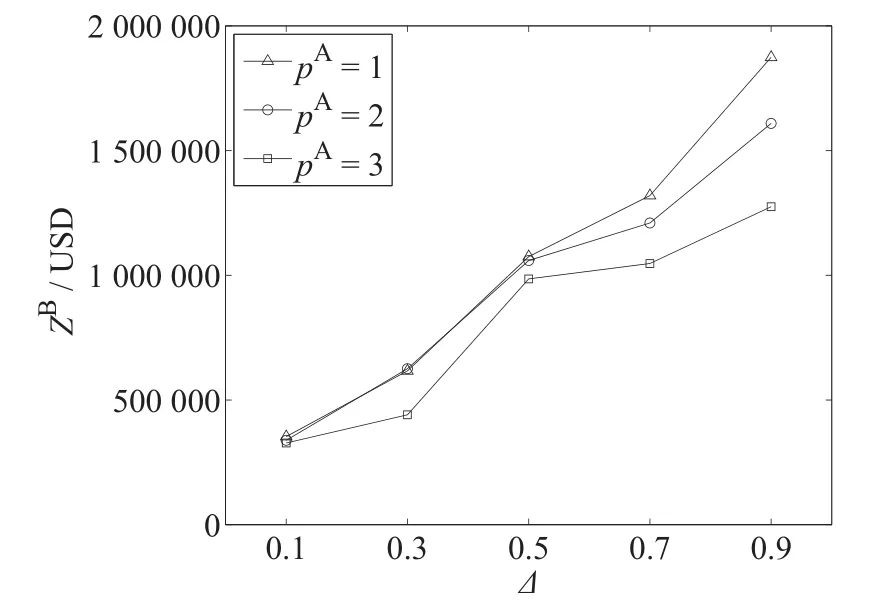
图2 不同定价的成本加成(Δ)对跟随者B利润(ZB)的影响Fig.2 The influence of cost plus for different pricing(Δ)on profits of follower B(ZB)

5.3.1 规模经济效应α对跟随者B利润ZB的影响

在Δ=0.5,Θ=0.004固定及pA={1,2,3}三种情景下,分析α={0.2,0.4,0.6,0.8,1}对跟随者B利润ZB的影响.由图1可知,α较小时的ZB显著高于α较大时的ZB.在α=0.2和α=0.4时,因跟随者B可通过建立多个枢纽港口享用更大的规模经济效应来捕捉到更多的市场机会.不论α大小,跟随者B的利润ZB随着pA增加出现了不同程度的减少,这是因为,pA＞1时领导者A同样可享用规模经济效应,将迫使跟随者B处于较不利的竞争位势.值得注意的是,在α=1时,跟随者B只能被动接受原有市场分配,除非枢纽港口之间的运输存在一定的规模经济效应α＜1,这足以见证规模经济效应α对跟随者B利润ZB的重要性.

5.3.2 成本加成Δ对跟随者B利润ZB的影响

在α=0.4,Θ=0.004固定及pA={1,2,3}三种情景下,分析Δ={0.1,0.3,0.5,0.7,0.9}对跟随者B利润ZB的影响.由图2可知,Δ与ZB之间存在一定正相关性,因跟随者B在某些航线上可捕捉的市场机会与托运人对运输价格的灵敏度参数Θ有重要联系.即使领导者A通过设计pA=3的轴–辐式海运网络来降低单位运输成本但因Δ较大,跟随者B完全可通过建立更多的枢纽港口来争取利润ZB.反之,这也说明了领导者A具有较大的市场控制权,其完全可通过调小Δ使跟随者B在竞争中处于危险位势;特别在Δ=0.1时,跟随者B几乎很难进入市场.值得注意的是,在pA=3时,不论Δ大小,跟随者B利润ZB相比pA=1或pA=2时存在不同程度的减少,与5.3.1节的结论一致.

5.3.3 灵敏度参数Θ对跟随者B利润ZB的影响

在pA=2,Δ=0.5固定及α={0.2,0.4,0.6,0.8,1}五种情景下,分析Θ={0.001,0.004,0.007,0.010,0.013}对跟随者B利润ZB的影响.由图3可知,Θ=0.013时ZB最大,因跟随者B可通过建立大量的枢纽港口来吸引更多对单位运输价格非常敏感的托运人,而pA=2和Δ=0.5时,领导者A仅可为托运人提供相对适中的单位运输价格.值得注意的是,在Θ降至Θ=0.004时,与领导者A提供的单位运输价格形成最佳匹配状态,跟随者B难以利用轴–辐式海运网络优化来争取利润ZB;但是,在Θ进一步降至Θ=0.001时,跟随者B反可通过提高来获取丰厚利润ZB.直观预测,领导者A定价的Δ越大,应越有利于跟随者B进入市场,这与5.3.2节的结论一致.

表4 不同单位运输成本C比较下跟随者B的最优定价决策PTable 4 The optimal pricing decision Pof the follower B by the comparison of different unit transportation cost C

表4 不同单位运输成本C比较下跟随者B的最优定价决策PTable 4 The optimal pricing decision Pof the follower B by the comparison of different unit transportation cost C

枢纽港口 航线连接 成本/USD 价格/USD 市场份额% 利润/USD领导者A 8,16 3→8→16→19 472.40 708.60 58.42 135 789.32跟随者B 2,4,8,10,11,12,14,15,16,17,18,19,20 3→2→19→19 427.80 793.65 41.58 149 672.43领导者A 8,16 5→8→8→4 184.00 276.00 85.26 187 285.56跟随者B 2,4,8,10,11,12,14,15,16,17,18,19,20 5→10→10→4 422.00 714.77 14.74 50 154.04

6 结束语

本文针对同一海运市场上不同地位的海运企业–领导者与跟随者在战略层面上设计以枢纽港口为中心的轴–辐式海运网络时引起的竞争问题,结合二者在战术层面上成本导向与需求导向的定价策略,即成本加成与基于Logit模型表示托运人选择行为的定价决策,分别建立了固定的规模经济效应、基于路径–流量的变量下领导者成本最小化与跟随者利润最大化的轴–辐式海运网络设计与定价决策模型.利用CPLEX直接对领导者的离散枢纽选址模型进行求解;对于跟随者的连续枢纽选址模型,基于Lambert W函数推导可得的最优定价决策,再利用连续化方法NCP函数、凝聚函数和增广Lagrange乘子罚函数法对其求解.最后,通过算例与遗传算法的计算结果对比,验证了所设计模型算法的适用范围与求解性能.不同情境下跟随者的轴–辐式海运网络设计与定价决策的仿真结果显示:跟随者可通过建立多个枢纽港口享用较大的规模经济效应吸引大量对价格敏感的托运人以获取丰厚的利润,但是,在领导者经营较多的枢纽港口且定价的成本加成较低时,跟随者较难进入市场;此外,海运市场上始终存在着一些愿意支付更高价格的托运人,跟随者利润最大化目标要求它不能因争取更多的托运人而降低定价决策.

上述仿真结果可为我国海运企业进行合理的轴–辐式海运网络设计与定价决策以争取更多的市场机会,进而参与国际竞争提供参考,但研究中考虑的竞争因素、网络因素和选择行为因素仍比较有限,比如多个港口挂靠的航线连接、服务时间(单位运输时间、港口装卸时间等)、服务频率、枢纽港口的拥堵状况、托运人的不同喜好等,考虑更多现实因素的轴–辐式海运网络设计与定价决策研究仍有待进一步深化.