在“综合与实践”活动中培养学生数学核心素养——“涂色的正方体”教学实录及评析

◇执教/张继刚 评析/刘富森

一、情境引入、提出问题

1.复习正方体特征。

师：（课件出示旋转的正方体）请同学们看屏幕，这是什么图形？它有哪些特征？

（生答略）

2.问题情境。

（课件出示：在一个三胞胎的家庭里，妈妈买了一块正方体形状的面包。她把面包的表面涂满红色奶油，然后把这块面包平均分成了很多小块，让每个孩子选一种。老大非常喜欢吃奶油，老二比较喜欢吃奶油，老三只喜欢吃一点奶油，你认为他们三兄弟会选哪一种？为什么）

师：谁有答案？请你上来指一指。

生：老大会选顶点处的一小块，因为每个顶点处，有3面涂有奶油。

（利用平板电脑，教师引导学生在课件里拖出小正方体，该正方体会变成蓝色）

师：老二呢？老三呢？

（生答略）

师：通过这几位同学的回答，你发现涂三面，涂两面，涂一面的小正方体，分别在原来大正方体的哪个位置？

（生答略）

3.提出问题。

师：老师根据这个情境提出了一个问题，你还能提出什么数学问题？

生：老大、老二、老三选的面包分别有多少小块？

师：这个问题的答案是什么呢？学完今天的涂色的正方体，你就会明白了。

【评析】从生活情境引入，激发学生学习兴趣和探究欲望，调动了学生的生活经验。同时，让学生明确三面涂色、两面涂色、一面涂色的小正方体在原来大正方体上的位置，为后面找规律和建模打下坚实的基础。本环节还培养学生分析问题、发现问题、提出问题的能力。

二、尝试解决、发现规律

1.每条棱上个数是3和4的正方体。

（1）小组合作。

师：为了研究方便，我们把这个涂满红色的大正方体看作刚才的面包。我们就先来研究每条棱上个数是3和4这两种简单的情况，看看这四类小正方体个数有什么规律。

师：现在我们小组合作来找规律。谁来读一下要求？

（出示小组合作要求：①先观察手中每条棱上个数是3的正方体，猜想每类小正方体的个数，再动手拆或者数，验证数据，最后填表1的第二行。②先观察手中每条棱上个数是4的正方体，再猜想每类小正方体的个数，然后填第三行，最后利用平板电脑在课件里拖动小正方体检查所填数据。③组长带领组员观察表中数据，你能发现什么规律？选出代表汇报）

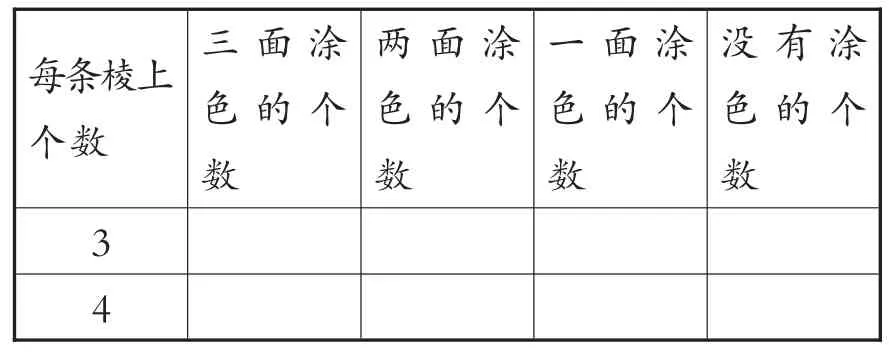
表1

（学生合作完成，教师巡视，并使用平板电脑互动传屏）

（2）全班汇报。

（学生上台一边汇报，一边在屏幕上点出符合要求的小正方体）

师：哪组来汇报一下三面涂色个数的规律？

生：三面涂色的小正方体都在顶点处，一共有8个。

师：哪组来汇报一下两面涂色个数的规律？

生：它的规律是：都是每条棱上个数去掉两端后，中间的个数×12。每条棱上个数是3的正方体，因为每条棱中间有1个两面涂色的小正方体，所以用 1×12=12（个）。每条棱上块数是 4的正方体，每条棱中间有2个两面涂色的小正方体，所以用 2×12=24（个）。

师：哪组来汇报一下一面涂色个数的规律？

生：它的规律是：每个面的中间不靠边的个数×6。每条棱上个数是3的正方体，因为每个面的中间有1个一面涂色的小正方体，所以用1×6=6（个）（板书：1×6=6）。每条棱上个数是 4 的正方体，每个面的中间有4个一面涂色的小正方体，所以用 4×6=24（个）。

（板书：4×6=24）

师：你这个4怎么得出来的？

生：2×2=4，在前面这个面中一行有2块，一共有2行，所以用2×2=4。

师：为了方便我们找规律，我们将上面的1×6=6改一下，怎么改？

生：1×1×6=6。

（板书：1×1）

师：哪组来汇报一下你们是怎么找出没有涂色的小正方体个数？

生：将每条棱上个数是3的正方体，外面涂色的都剥掉，数出没有涂色的是1个。每条棱上个数是4的正方体，推理得出，一共有8个没有涂色的。我们使用平板电脑拖动小正方体检查出它有8个没有涂色的。

师：你的空间想象能力真强！我们一起拖动小正方体看一下。

师：这个正方体沿长去掉两边的两列，沿宽去掉两边的两列，沿高去掉上下的两层，剩下的就是每条棱上个数是2的小正方体没有涂色。

（教师引导学生拖动，演示将三面、两面、一面涂色的小正方体剥离出去的过程，如图1）

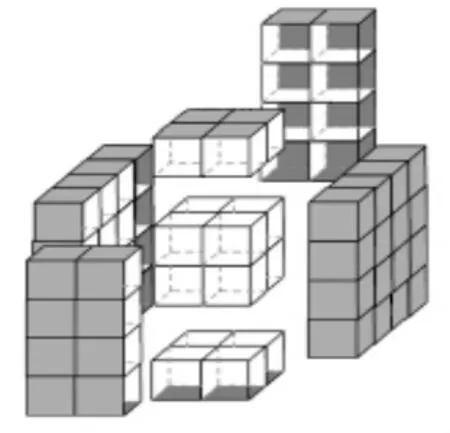
图1

师：这个8你是怎么得出来的？

生：2×2×2 得出来的。

师：我们还可以把 2×2×2 写成 23。

（板书：23）

师：对于这个正方体，怎么来说呢？请你边拖动小正方体，边讲解剥离的过程。

（生答略）

师：非常称职的小老师！可以看出大家的猜测是正确的。上面的1怎么改？

生：13。

师：这样就方便我们找规律了。没有涂色的小正方体有什么规律呢？

生：都是长、宽、高中去掉了2，每条棱上个数减2的差的立方。

【评析】通过学生的实物操作与平板电脑检验，让学生在头脑里建立表象。平板电脑的应用，将学生小组合作的情况实时地传到大屏幕上，实现移动投影仪的功能，方便其他组学生借鉴。活动单的填写，便于后面规律的抽象概括与归纳。本环节让学生经历观察、想象、比较等过程，让学生初步感知规律，同时获得“化繁为简”“分类计数”解决问题的经验，体会分类、数形结合等数学思想，培养了学生的空间想象力，发展了数学抽象、逻辑推理等能力。

2.每条棱上个数是5的正方体。

（1）提出猜想。

师：刚才我们通过操作交流找到了一些规律，那你能大胆猜想一下每条棱上个数是5的正方体上，这四类小正方体的数量吗？谁愿意来提出你的猜想？

生：三面涂色的个数是8,两面涂色的个数是 3×12=36，一面涂色的个数是 3×3×6=54，没有涂色的个数是33。

（2）操作与推理，验证猜想。

师：这些猜想正确吗？还需要我们去验证。谁能上来指着图验证这些猜想？

生：（点击顶点处的小正方体变为蓝色）三面涂色的就在每个顶点处，正方体有8个顶点，所以三面涂色的一共有8个小正方体。

师：恭喜你验证了第一个猜想是正确的！谁继续上来验证？

生：（点击棱上中间的小正方体变为黄色）两面涂色的每条棱上有3个，再乘12，就是一共的36个。

师：恭喜你验证了第二个猜想也是正确的！谁继续上来验证？

生：（点击面中间的小正方体变为绿色）一面涂色的每面有3×3=9（个），再乘6，就是一共的54个。

师：恭喜你验证了第三个猜想也是正确的！谁继续上来验证？

生：没有涂色的就是棱长是3的正方体，个数就是33=27。

（学生点击白板，分别剥离整列左右、上下、前后涂色的小正方体，露出没涂色的正方体）

师：你的逻辑思维能力真强！我们现在可以把“？”擦掉了。

【评析】提出猜想，验证规律，通过观察、比较、想象、推理等过程，经历“找规律”过程，培养学生的空间想象力，让学生体会数形结合、推理等数学思想。同时，也培养了学生的数学抽象、逻辑推理、数学运算、直观想象、数据分析等能力。

3.总结归纳。

（出示表2，表格下边有对应四类小正方体的显示相应颜色的图2）

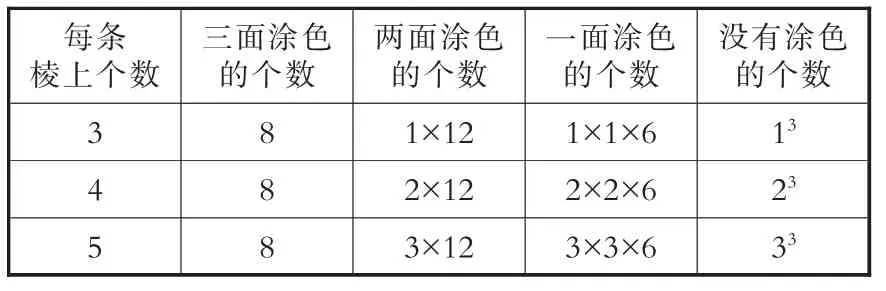
表2

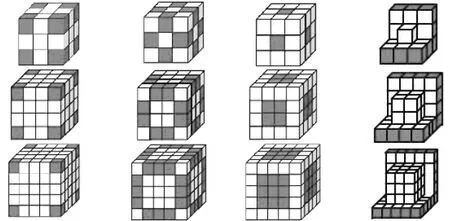
图2

师：我们通过观察、猜想、验证得出了一些规律，请同桌两人讨论归纳一下：每类小正方体的数量有什么规律？

（1）文字表示规律。

师：谁来汇报三面涂色的小正方体数量的规律呢？

生：三面涂色的在正方体顶点位置，所以有8个。

师：两面涂色的呢？

生：因为两面涂色的小正方体都在棱上，每条棱上个数减去2个顶点处的小正方体个数，有12条棱，所以两面涂色的小正方体就有每条棱上个数减2的差乘12个。

师：一面涂色的呢？没有涂色的呢？

（生答略）

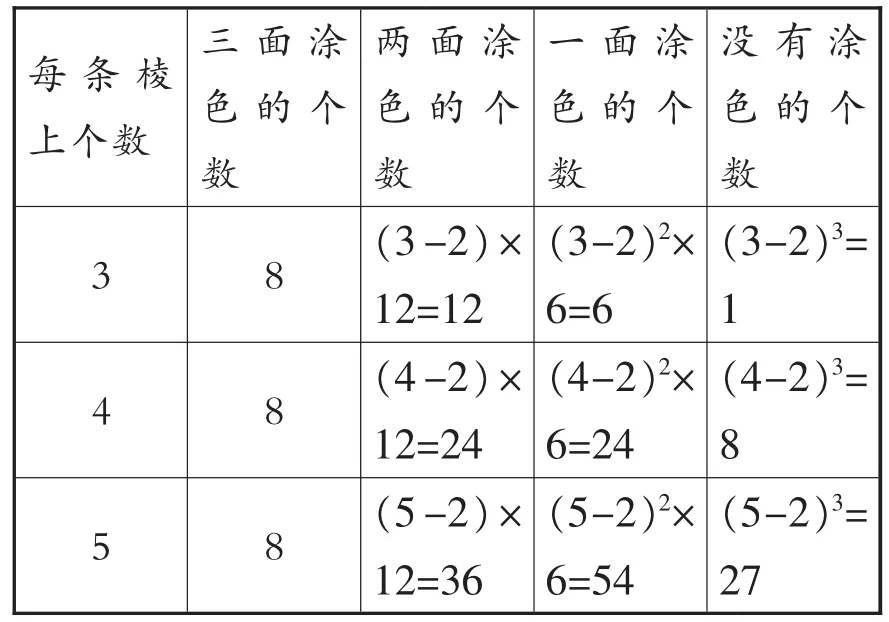
表3

（2）字母表示。

师：刚才我们推理归纳出了这些规律。如果正方体每条棱上的个数继续增加，为了把所有情况都表示出来，我们就请出我们的好朋友字母来帮忙。如果用n表示正方体棱上的个数，那么小正方体涂色规律可以怎么表示呢？独立思考半分钟。

师：谁来汇报一下你思考的结果？

[生答，师板书：8，（n-2）×12，（n-2）2×6，（n-2）3]

师：之前我们用文字叙述规律太麻烦，那用字母表示这些规律怎么样呢？

生：非常简洁！

师：这就是数学的简洁美！

【评析】通过比较、归纳等过程，经历“找规律”过程，让学生体会抽象、归纳、推理、模型、变中有不变等数学思想，积累数学思维的活动经验。用含有字母的式子表示规律，把学生的认知从特殊推向一般，培养学生的抽象概括能力，同时体现了数学的简洁美。

4.应用规律。（略）

【注：本课在2016年5月举行的“第二届全国小学数学文化优质课大赛暨课堂教学观摩研讨会”上获得全国一等奖。】