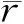The laminate layer solution to a class of Cauchy problem for nonlinear nonlocal singularly perturbed fractional order differential equation
2018-12-05,,
, ,
(1. Department of Mathematics, Shanghai University, Shanghai 200436, China;2. Department of Electronics and Information Engineering, Bozhou College, Bozhou 236800, China;3. Department of Basic, Hefei Preschool Education College, Hefei 230011, China;4. School of Mathematics & Computer Science, Anhui Normal University, Wuhu 241003, China)
Abstract:A class of Cauchy problems for the nonlinear nonlocal singular perturbation fractional order differential equation is studied. Firstly, the outer solution of the original problem is obtained. Secondly, using the stretched variables and the composing expansion method, the initial layers are constructed. Finally, using the theory of differential inequality, the asymptotic behavior of the solution to original Cauchy problem of nonlinear nonlocal singular perturbation fractional order differential equation is studied and the uniformly valid asymptotic estimation is discussed.
Key words:nonlinear; fractional order equation; singular perturbation
In the natural, many mathematical physics problems can be solved using the fractional order derivative. For example, the complicated seepage flow, the heat conduction phenomena and so on, they can be solved using the idea of fractional order derivative[1-3]. Fractional order derivative possesses its broad practice sense. But solving the nonlinear fractional order differential equation is very difficult. In this paper, we obtain asymptotic solution to the nonlinear fractional order differential equation using the singularly perturbed theory, and get its uniformly valid estimation using the theory of differential inequalities.
The nonlinear singular perturbation problem is a very attractive object in the academic circles[4-6]. Many asymptotic methods have been developed, including the boundary layer method, the method of averaging, the methods of matched expansion and the method of multiple scales. Recently, many scholars have done a great deal of work[7-11]. Using the method of singular perturbation and others, the authors studied also a class of nonlinear boundary value problems for the reaction diffusion equations, a class of activator inhibitor system, the shock wave, the soliton, the laser pulse and the problems of atmospheric physics and so on[12-29]. In this paper, we constructed asymptotic solution for the fractional order differential equation, and proved it’s uniformly validity
Consider the following singularly perturbed Cauchy problem ofmαthfractional order differential equation with two parameters:
0 (1) (2) whereΓis the Gamma function,αis a positive fraction less than 1. We need the following hypotheses: [H1]f(x,Tu) is a sufficiently smooth function with respect to their arguments in corresponding domains; [H2]fTu≤-δ<0, whereδis a constant. [H3] There is a sufficiently smooth bounded solutionU00(x)to the reduced equationcu-f(x,Tu)=0 for original problem (1)- (2). We first construct the outer solutionU(x) to the nonlinear nonlocal Cauchy problem (1)-(2). Let (3) Substituting Eq. (3) into Eq. (1), developingf(x,Tu) inεαandμα, and equating coefficients of the same powers ofεαiμαjto zero, Then we have cUij(x)-(fTu(x,TU00))TUij= i,j=0,1,…,i+j≠0 (4) where i,j=0,1,…,i+j≠0 And we assume that the above and below the negative subscript terms are zero. Thus from Eq. (4), we can obtainUij(x)(i,j=0,1,…,i+j≠0) successively. SubstitutingU00(x) andUij(x)(i,j=0,1,…,i+j≠0) into Eq. (3), we obtained the outer solutionU(x) for the original singular perturbation Cauchy problem (1), (2). But it do not satisfies initial condition (2), so that we need to construct the initial layer correction terms. Let i.e. (5) Thus Eq. (1) is (6) Lead into stretched varixbles[4-6] and set (7) where (8) (9) k=0,1,…,m-1 (10) i,j=0,1,…,i+j≠0 (11) i,j=0,1,…,k=0,1,…,m-1 (12) (13) wherelij(i,j=0,1,…) are positive constants. Thus, we can obtain the formally asymptotic expansion of the solution to Cauchy problem (1), (2): (14) Theorem1 Under the hypotheses [H1]-[H3], andμm/n/ε→0 asε→0, then there exists a uniformly valid asymptotic expansion (14) for the solutionuto nonlinear singular perturbation Cauchy problem (1)-(2). Proof Introducing two auxiliary functions: (15) where andris a large enough positive constants. From Eq. (15), obviously, we have (16) From the hypotheses and Eq. (13), it is easy to know that, there exists a large enough positive constantM1, andε,μsmall enough, takingr≥M1, we have k=0,1,…,m-1 (17) Now we prove that 0 (18) 0 (19) In fact, from the hypotheses and Eqs. (13), (15) forεandμsmall enough, there is a positive constantM≥M1, such that f(x,TPM)-f(x,T(PM-rξM+1))≤ cU00-f(x,TU00)+ f(0,T(U00))+ i.e. ε=ξmηm-n,μ=ξn (20) Thus Eq. (1) is (21) Lead into stretched variables: and set u=U+V (22) where (23) Substituting Eqs. (22), (23) into Eqs. (21), (2), developing the nonlinear termf(x,T(U+V)) inξα,ηαand equating coefficients of the same powers ofξαiηαjto zero, we have f(0,T(U00+V00))-f(0,T(U00)) (24) (25) i,j=0,1,…,i+j≠0 (26) k=0,1,…,n-1 (27) whereGij(i,j=0,1,…,i+j≠0) are inductively known functions, whose constructions are omitted. From the hypotheses and theory for characteristic equation of corresponding linear fractional order differential equations with constant coefficients, the fractional order differential equations Cauchy problems (24), (25) and (26), (27), we can obtain solutionsVij(τ),i,j=0,1,… successively and possess initial layer behavior. i,j=0,1,…,0<ξ≪1 (28) wherekij(i,j=0,1,…), are positive constants. SubstitutingVij(τ),i,j=0,1,… into Eq. (23), we obtain the first initial layer correction termV(τ) of the solutionu(x)to the original Cauchy problem (1), (2). But Eq. (22) do not satisfies initial condition (2) fork=n,n+1,…,m-1, so that we also need to construct the second initial layer correction term. From Eq. (21), we have (29) Lead into stretched variables: and set u=U+V+W (30) where (31) Substituting Eqs.(30), (31) into Eqs. (29), (2), developing the nonlinear termf(x,T(U+V+W)) inζα,ηαand equating coefficients of the same powers ofζαiηαjto zero, we have (32) k=0,1,…,m-1 (33) i,j=0,1,…,i+j≠0 (34) i,j=0,1,…,i+j≠0,k=0,1,…,m-1 (35) i,j=0,1,…,0<ζ≪1 (36) Therefore, we can obtain the formally asymptotic expansion to the Cauchy problem (1), (2): 0<ε,μ,ξ,η,ζ≪1 (37) whereξ=μ1/n,η=(ε/μm/n)1/(m-n),ζ=(ε/μ)1/(m-n)andε/μm/n→0, asμ→0. We prove the following theorem: Theorem2 Under the hypotheses [H1]-[H3], andε/μm+n→0 asμ→0, then there exists a uniformly valid asymptotic expansion (37) for the solutionuto nonlinear singular perturbation Cauchy problem (1)-(2). ProofIntroducing two auxiliary functions: (38) where max(εMμM+1,εM+1μM,ξMηM+1,ξM+1ηM,ζMηM+1,ζM+1ηM) From Eq. (28), obviously, we have (39) k=0,1,…,m-1 (40) Now we prove that 0 (41) 0 (42) cU00-f(x,TU00)+ We also to see that from Eqs. (28), (36), expansion (37) possess two thin layer terms nearx=0, their thickness areO(ξ)=O(μ1/n) andO(ζ)=O((ε/μ)1/(m-n)) respectively. And due toζ/ξ=(ε/μm/n)1/(m-n)→0,μ→0, then it constitutes the laminate layer solution phenomenon.
1 The Outer Solution U
2 As μm/n/ε→0,ε→0




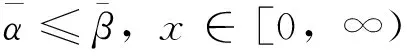

3 As ε/μm/n→0, μ→0
3.1 Let ξ=μ1/n, η=(ε/μm/n)1/(m-n)
3.2 Let ζ=ξη