带损伤简支梁力学响应的解析*

2018-12-05董文奇杨怡王玉爽黄炽辉

中山大学学报(自然科学版)(中英文) 2018年6期

董文奇, 杨怡, 王玉爽，黄炽辉

(华南理工大学土木与交通学院，广东广州 510641 )

对于损伤简支梁的研究，目前主要集中在对损伤的识别或者检测上。由于简支梁的固有频率等信息会因为损伤的存在而发生改变，因此很多学者都是通过损伤简支梁的模态、固有频率等来判断损伤的程度以及损伤的位置等。如：刘习军等[1]通过小波分析对简支梁进行损伤识别研究，定义了能量曲率差损伤指标用于损伤的识别与定位，提出了基于小波子带信号的能量曲率变化损伤识别方法。José Fernández-Sáez等[2]基于固有频率的数据，对弯曲振动下带有单个裂纹的简支梁进行了损伤识别的研究；刘宇飞等[3]利用平均曲率模态对移动荷载激励下简支梁的局部损伤进行了识别研究。他们采用的缺口平滑拟合技术不需要事先获得损伤前简支梁的激振数据，而且可以用于多移动荷载同时激励的情况。Xia等[4]则提出了一种基于长应变传感技术和主成分分析技术的损伤检测方法，并应用于损伤简支梁中。胡磊等[5]提出一种基于改进萤火虫算法的结构损伤识别方法，克服了萤火虫算法在高维目标函数中寻优能力不足的问题，并且提高了计算精度。

对于损伤简支梁的研究不仅仅局限于损伤识别与检测，有不少学者通过有限元法分析了损伤简支梁的振动性能。罗裴[6]通过有限元分析研究了损伤简支梁在单个以及多个单元损伤时的振动特性；Fu[7]给出了带有开关裂纹的简支梁桥，在受到地震激励和移动列车作用时的动力响应数值解，并且讨论了车重以及车速对振幅的影响；徐平[8]通过将裂缝损伤简化成矩形凹槽，对局部裂纹损伤简支梁的曲率模态特性进行了研究，求解出受损简支梁的特征值以及模态振型的解析表达式；姜海波等[9]就对带边界条件的损伤简支梁的振动模态进行了推导。

这些研究都是借助有限元法进行数值模拟，而理论研究报道甚少。本文将U变换法和有限元法相结合，对具有刚度损伤的均质简支梁的静力和动力问题进行了解析研究。U变换法，作为循环周期结构理论分析的有效方法，被广泛应用于对周期结构的解析研究[10-12]，其优点在于能够给出结构控制方程对应的精确解析解。本文首先将损伤梁进行对称扩展，构造具有结构上循环周期性的等价系统；根据有限元法给出结构的控制方程，并对挠度变量运用变换，得到降阶后的用广义位移表示的控

制方程；接着，以线性梁单元和均布荷载为例，推导各节点解析形式的位移；然后，讨论损伤位置和损伤程度对结构变形的影响，再对结构的自由振动方程进行分析，给出固有频率的解析解。

1 结构模型

考虑一长度为L的均质简支梁，利用有限元法对其进行单元划分，划分成n个长度为a的相同单元。这样简支梁就可以看成是具有n个子系统的周期性结构，如图1所示，其中j为单元的编号，F(x)为结构所受荷载。

图1 具有n个相同单元的简支梁Fig.1 Simply supported beam with n elements

为了应用U变换法对该结构进行分析，需要构造一个等效的循环周期系统。在图1所示的简支梁的右边进行结构扩展，去掉连接处的支座，并且在扩展结构上施加与原结构反对称的荷载，得到具有2n个单元的结构，如图2所示。该结构的左半边梁的结构属性、荷载情况和边界条件与原结构完全相同，即图2结构是图1简支梁的等效结构。当单元数n→∞时，结构的左右端可以看成相互连接，在数学上可以看成是首尾相连的具有2n个子结构的循环周期结构。

图2 原周期系统的等效系统Fig.2 Equivalent system with 2n substructures

图3 受均布荷载的等效系统Fig.3 Equivalent system subjected to uniformly distributed load

2 控制方程

对于单元划分后的简支梁，假设其第j1个单元发生了刚度损伤，刚度损伤量为[ΔK]，不考虑质量损伤。为了方便讨论，假设简支梁受到均布荷载的作用，其荷载幅值为p0，如图3所示。

在均布荷载的作用下，每个单元的外加荷载向量可以表示为：

j=1,2,...,n

(1)

根据反对称性，有

j=n+1,...,2n

(2)

而对于第j1个单元，也就是损伤单元，由于刚度的损伤，在同样外加荷载作用下其位移向量会增大。为了避免直接用刚度损伤来讨论，可以将这种由刚度损伤引起的失谐条件用附加荷载的形式来表示，即

(3)

{δ}j1为损伤单元j1的位移。根据反对称性，有

(4)

在式(3)、(4)中，{δ}j1表示单元j1的位移向量。而对于任意单元的位移向量，可以表示为：

(5)

其中，式(5)中的{δ1}和{δ2}分别表示单元j左右两个节点的位移向量，w、θ分别是节点挠度和截面转角。

因此，单元所受到的总荷载可以表示为外加荷载与附加荷载之和，即

(6)

其中

(7)

(8)

下面通过能量法来构建控制方程。当简支梁在受到静载作用时，其总势能是守恒的。根据功能关系，整个等效系统的总势能可以表示为：

(9)

其中，πj为单元j的势能：

(10)

在式(10)中，[K]e表示无损单元的刚度矩阵，{F}j和{δ}j分别表示荷载向量和位移向量，向量上的横线表示共轭。

对位移向量进行U变换[13]，即令

(11)

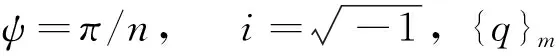
(12)

式中，q1,q2是{q}m的两个分量，均为2×1的向量。

把式(11)代入到(5)，(9)和(10)中，可以得到用广义位移表示的总势能，即：

(13)

其中，{F}m为广义荷载向量，

(14a)

(14b)

(14c)

由连续性条件，有：

{δ1}j+1={δ2}j

(15)

由式(11)，(12)和(15)得：

{q2}m=eimψ{q1}m

(16)

根据连续性条件(16)，有

{q}m=[T]m{q1}m

(17)

其中，[T]m为转换矩阵：

(18)

把式(17)和(18)代入到式(13)，结构总势能的表达式变为：

(19)

(20)

(21)

依据简支梁的势能守恒，把方程(19)代入势能变分方程：

δΠ=0

(22)

可以得到

(23)

控制方程通过U变换后，得到m个用广义位移{q1}m表示独立的方程。控制方程得以解耦。

3 位移计算

引入损伤因子β，表示刚度损伤的程度：

[ΔK]=-β[K]e, 0≤β<1

(24)

由式(14)可知

(25)

把式(25)代入(21)，得：

(26)

其中

(27a)

(27b)

现选取线性梁单元作为划分单元，其单元刚度矩阵为：

(28)

其中，EI是无损梁的弯曲刚度。把式(28)代入(20)，可得：

(29)

式(23)可以改写为

(30)

其分量形式为：

(31)

其中

[(1-e-imψ)·12(w1j1-w2j1)+

6a(1-e-imψ)(θ1j1+θ2j1)]

[(1+e-imψ)·6a(w1j1-w2j1)+

(4a2+2a2e-imψ)θ1j1+(2a2+4a2e-imψ)θ2j1]

(32)

由式(31)可以得到：

(33)

由式(11)可知

(34)

把式(32)、(33)代入(34)，可以得到节点挠度和截面转角的表达式：

(35a)

(35b)

其中

Am=(e-i(ji-1)mψ-e-i(2n-ji)mψ)·12(1-e-imψ)·

(w1j1-w2j1)+(e-i(ji-1)mψ-e-i(2n-ji)mψ)·

6a(1-e-imψ)(θ1j1+θ2j1)

Bm=(e-i(ji-1)mψ-e-i(2n-ji)mψ)·6(1+e-imψ)·

(w1j1-w2j1)+(e-i(ji-1)mψ-e-i(2n-ji)mψ)·

(4a+2ae-imψ)θ1j1+(e-i(ji-1)mψ-e-i(2n-ji)mψ)·

(2a+4ae-imψ)θ2j1

(36)

从式(35)中可以看出，当β=0时，等号右边的第一项应等于简支梁在没有受损时的节点位移，与文献[13]的结果完全一致。而等号右边的第二项则是由于损伤单元的刚度损伤而引起的位移增量，其大小与损伤程度、损伤单元的位置以及外加的荷载有关。由于Am和Bm中包含了损伤单元的位移向量，因此需要先求解出损伤单元两个节点的位移才可确定其他节点的位移。

在式(34)中，分别令j=j1、j=j1+1，并且取实部计算，可得到损伤单元的的位移表达式：

(37)

(38)

其中,Re表示取实部计算。式(37)-(38)由四个方程组成，联立这四个方程便可以求解出损伤单元的四个节点位移。然后将其代回式(34)-(36)，即可得到所有节点的位移。

4 损伤对变形的影响

4.1 损伤程度对变形的影响

从上述推导可以知道，损伤结构的位移增加量受单元损伤程度、损伤位置以及荷载大小的影响。本小节先讨论简支梁的弯曲变形随损伤程度的变化。为方便计算，假设简支梁均分为11个单元，损伤发生在中间单元，即n=11,j1=6，如图(4)所示，其中①、②、③……表示节点编号。

图 4 中间单元损伤的简支梁Fig.4 Simply supported beam with a damaged element at the span center

将n=11,j1=6代入式(37)-(38)，并应用对称性，可解得损伤单元的位移分量为:

(39)

把损伤单元位移(39)代回(35)，就可以求得所有节点的挠度和转角。为讨论损伤程度对变形的影响，取0.1作为步长，分别计算β=0～0.5时各个节点的挠度和截面转角，计算结果见表1-2。表1-2只给出了简支梁左半部分6个节点的位移，表1中第一个节点的挠度均为0，因此没有列出来；结构右半部分的节点位移与左半部分关于简支梁中轴线对称。

为检验理论计算结果的可靠性，本文使用有限元计算软件ABAQUS进行数值分析。图4所示结构的有限元模型详见图5。在图中，模型长度为11，共分成11段，中间一段有刚度损伤。模型采用Beam21梁单元，横截面设置为1×1的矩形截面。模型总共划分为110个单元。为进行无量纲化分析，无损单元的弹性模量设置为175 692，用中间段的弹性模量按比例减小来表示刚度损伤；不设置泊松比。在结构上施加方向向下的均布荷载，集度为1；在两端施加简支梁约束。计算模型的变形，部分节点挠度和截面转角列于表1-2的圆括号内。

表1 节点挠度计算结果1)
Table 1 Results of nodal deflections

β②③④⑤⑥03.728 17.120 49.903 711.873 112.891 9(3.794 6)*(7.240 2)(10.063 4)(12.059 4)(13.091 6)0.13.785 37.234 910.075 412.102 013.178 0(3.890 5)(7.431 9)(10.351 0)(12.442 9)(13.570 9)0.23.856 97.378 010.290 012.388 213.535 8(3.923 4)(7.497 7)(10.449 7)(12.5745)(13.735 4)0.33.948 97.561 910.566 012.756 113.995 7(4.015 4)(7.681 7)(10.725 7)(12.942 4)(14.195 3)0.44.071 57.807 210.933 913.246 714.608 9(4.138 0)(7.927 0)(11.093 6)(13.433)(14.808 5)0.54.243 28.150 611.449 013.933 515.467 4(4.309 7)(8.270 3)(11.608 7)(14.1197)(15.666 9)Multiplier(p0L4/EI)×10-3

1)*表示圆括号内数值为有限元计算结果。

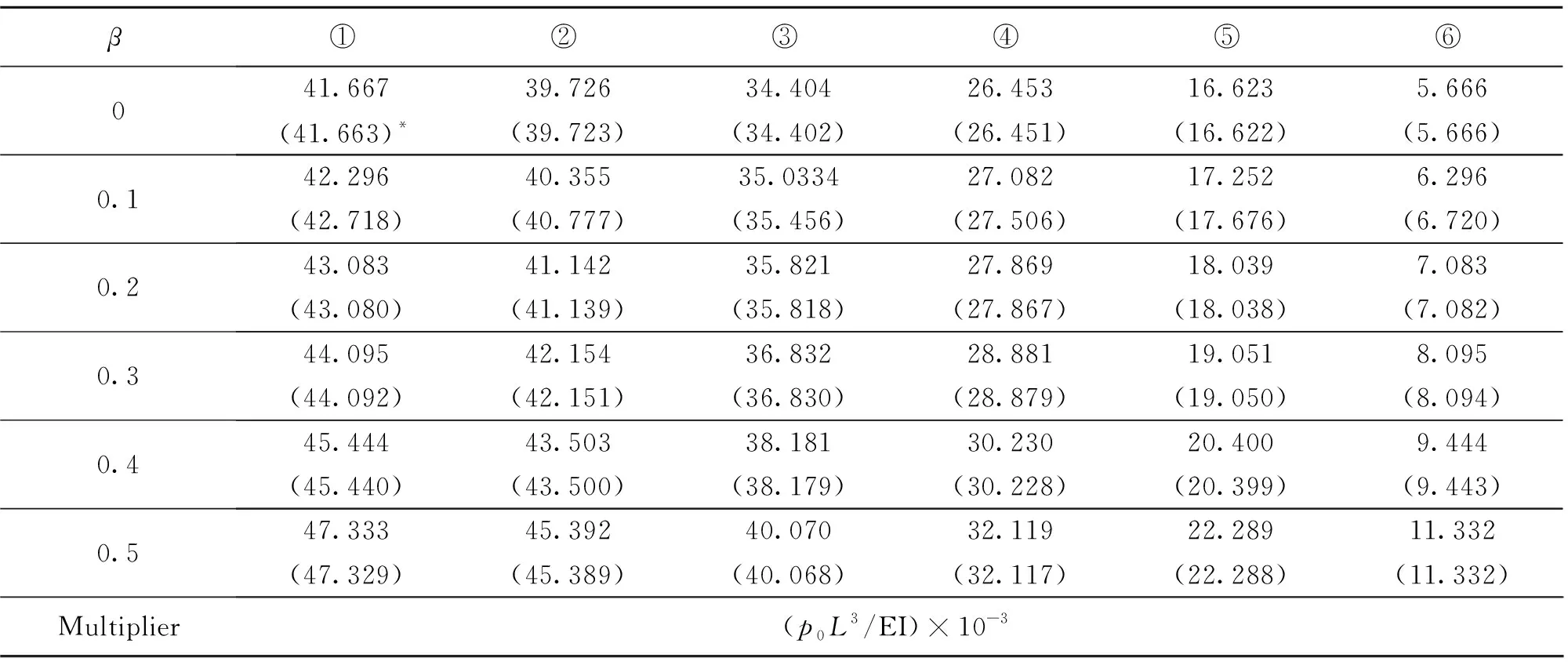
表2 截面转角计算结果1)Table 2 Results of cross-sectional angles

1)*表示圆括号内数值为有限元计算结果。

图5 (a) 无损伤有限元模型，(b) 带损伤有限元模型Fig.5 Finite element models (a) without damage and (b) with damage

由表1-2可以看出，挠度的理论计算与有限元计算结果的最大相对误差发生在损伤程度为0.1时的6号节点，为2.98%。转角计算结果的最大相对误差发生在损伤程度为0.1时的6号节点处，为6.73%。理论分析采用欧拉梁模型，不考虑截面的尺寸和剪切变形，有限元分析需设置模型的横截面形状和尺寸，会产生剪切变形，这就造成了两种计算的相对误差。对比发现，相对误差在可接受范围内，因此本文的计算结果是可信的。

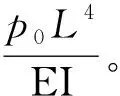
图6 损伤程度对结构变形的影响Fig.6 Influences of damage degree on structural deformation

图7分析了各节点在不同损伤程度下的挠度增量，图中横坐标表示损伤程度，纵坐标表示挠度增量。由图7可知，当β=0.1～0.3，挠度增量与损伤程度是线性关系；当β>0.3时，挠度增大速率提高。图8则是各节点在不同损伤程度下的转角增量图，由于在相同损伤程度下各节点的转角增量一样，所以图中只有一条曲线。其变化趋势与图7相似。

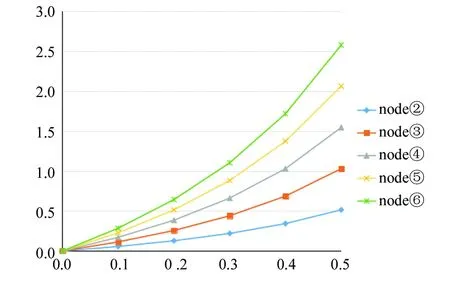
图7 各节点在不同损伤程度下的挠度增量Fig.7 Deflection increments of nodes under different damages

图8 各截面在不同损伤程度下的转角增量Fig.8 The increments of the cross-sectional angles under different damages

从表1-2和图6以及图7、图8可以看出：(1) 在损伤位置以及外加荷载不变的情况下，简支梁的节点挠度和截面转角会随着损伤程度的增加而增大，且增大的速率也会提高；(2) 节点的位置越靠近简支梁的中心，因刚度损失而引起的挠度的增量会越大，而转角的增量基本不变。

4.2 损伤位置对变形的影响

下面讨论简支梁变形随损伤位置的变化规律。令n=11，β=0.5，分别计算损伤从第一个单元往跨中方向移动时各节点的挠度，即j1=1～6。计算结果如表3所示。当j1=7～12时，可利用对称性得到梁的变形情况。根据表3的计算结果，通过二次插值可以得到β=0.5,j1=1～6时简支梁的挠曲线，如图9所示。

图9 β=0.5时损伤位置对结构变形的影响Fig.9 Influences of damage location on structural deformation when β=0.5

由表3以及图9可知：(1) 当损伤程度不变时，随着损伤单元从支座往跨中移动，节点的挠度会增大，且增大的速率也会提高。当损伤单元为中心单元时，挠度的整体增量取得最大值；(2) 随着损伤单元从左往右移动，最大挠度的位置也会从左往右发生轻微的偏移。当损伤单元为中心单元时，最大挠度位于简支梁的跨中；(3) 越靠近损伤单元的节点位移受到损伤单元的影响越大。因此，当损伤位置不同时挠曲线出现了交叉的现象。

表3 β=0.5时节点挠度Table 3 Results of nodal deflection when β=0.5

5 固有频率

5.1 自由振动方程

(40)

按照第3节的方法，对式(40)运用U变换，得到：

(41)

(42)

(43)

自由振动时，每个单元的节点位移可以写成{δ}jeiωt，{δ}j为t时刻单元j的节点位移向量。这样附加荷载可以表示为：

{F}j′ = -[ΔK]j{δ}jeiωt=βj[K]e{δ}jeiωt

(44)

e-i(2n-j1)mψ[K]e{δ}2n+1-j1)eiωt

(45)

把式(45)代入(21)，可以得到：

(46)

5.2 固有频率的计算

利用方程(45)求解结构的固有频率，可以令：

qm1=Qm1eiωt,qm2=Qm2eiωt

(47)

其中,Qm1,Qm2表示时刻t时的广义振幅。把式(47)代入(43)，并利用式(12)可得：

(48)

又因为

{q1}m={Qm1,Qm2}T

(49)

把式(49)、(46)代入(48)中，可以得到：

(50)

(51)

根据结构的反对称，对于任意时刻t，有：

[K]e{δ}j1=-[K]e{δ}2n+1-j1

(52)

由U变换可知，

(53)

令j=j1，并由式(47)、(51)以及(53)可得：

(54)

再令j=j1+1，重复上面的算法，得：

(55)

式(54)和(55)的等号的两边都包含了损伤单元的节点位移，联立这两个式子，可以消去损伤单元的节点位移，进而求解出结构的固有频率ω。

为了方便计算，考虑线性梁单元的质量集中在两端节点上的情况，不考虑转动惯性。线性梁单元的集中质量矩阵可以表示为：

(56)

其中，ρ表示单位长度梁的质量。把式(56)代入(42)中，可以得到广义质量矩阵：

(57)

再将式(57)、(18)、(28)以及(29)分别代入到式(54)-(55)中，可得：

(58)

(59)

其中，

Cm1=(1-ei(2j1-1)mψ)·12(1-e-imψ)(w1j1-w2j1)+

(1-ei(2j1-1)mψ)·6a(1-e-imψ)(θ1j1+θ2j1)

Cm2=(1-ei(2j1-1)mψ)·6a(1+e-imψ)(w1j1-w2j1)+

(1-ei(2j1-1)mψ)(4a2+2a2e-imψ)θ1j1+

(1-ei(2j1-1)mψ)(2a2+4a2e-imψ)θ2j1

Cm3=(eimψ-ei2j1mψ)·12(1-e-imψ)(w1j1-w2j1)+

(eimψ-ei2j1mψ)·6a(1-e-imψ)(θ1j1+θ2j1)

Cm4=(eimψ-ei2j1mψ)·6a(1+e-imψ)(w1j1-w2j1)+

(eimψ-ei2j1mψ)(4a2+2a2e-imψ)θ1j1+

(eimψ-ei2j1mψ)(2a2+4a2e-imψ)θ2j1

(60)

把式(58)-(59)展开并且取实数，再通过移项合并，可以得到四个方程组成的齐次方程组。写成列阵相乘的形式，可以表示为：

[A]m{δ}j1=0

(61)

其中，[A]m为四阶的系数方阵，表示为：

(62)

其各个元素是：

Sm1=a3(2+cosmψ)(1-ei(2j1-1)mψ)12(1-e-imψ)

-i3a2sinmψ(1-ei(2j1-1)mψ)6a(1+e-imψ)

Sm2=a3(2+cosmψ)(1-ei(2j1-1)mψ)6a(1-e-imψ)

-i3a2sinmψ(1-ei(2j1-1)mψ)(4a2+2a2e-imψ)

Sm3=a3(2+cosmψ)(1-ei(2j1-1)mψ)6a(1-e-imψ)

-i3a2sinmψ(1-ei(2j1-1)mψ)(2a2+4a2e-imψ)

Sm4=i3a2sinmψ(1-ei(2j1-1)mψ)·12(1-e-imψ)+

6a(1+e-imψ)

Sm5=i3a2sinmψ(1-ei(2j1-1)mψ)·6a(1-e-imψ)+

(4a2+2a2e-imψ)

Sm6=i3a2sinmψ(1-ei(2j1-1)mψ)·6a(1-e-imψ)+

(2a2+4a2e-imψ)

(63)

为了使得方程(61)的位移向量{δ}j1有非零解，必须满足系数方阵[A]m的行列式等于零，即：

(64)

展开式(64)后就可以得到关于ω2的频率方程，其正实数解便是ω2的取值。显然，由于行列式的元素中包含有β和j1，ω2与单元刚度的损伤程度以及损伤位置有关。

作为算例，假设单元损伤发生在简支梁的中心单元，令n=3，5，7，9，损伤因子β=0.5，代入式(64)，可以求得固有频率，见表4所示。由表4可知，当发生刚度损伤时，简支梁的固有频率会降低；若划分的单元数越多，固有频率越大，越接近无损时的固有频率，这是因为随着单元划分越细，刚度损伤占整个结构的比重就越小。