非线性系统准周期振动的多时间尺度IHB法*

张丹伟，刘济科，黄建亮

(中山大学工学院应用力学与工程系，广东 广州 510275)

在工程技术领域中，许多运动系统在多个外激励作用下，往往会产生周期与准周期振动。对于准周期振动，其系统的振动中包含了多个不可公约的响应频率，在长时间内不可预测，且对初始条件非常敏感。此类振动不仅会导致结构产生噪音，甚至会造成结构的失稳与破坏，在工程上会产生较大的安全隐患。因此，研究准周期运动及其产生的机理具有重要的理论与实际意义，受到了许多学者的关注。

Huang等[1]和Abe[2]分别研究了耦合斜拉悬索在1∶2和1∶1内共振条件下的Hopf分岔，Huang等[1]还利用数值法研究了悬索的准周期振动。Gan等[3]利用该斜拉悬索模型分析了输液管的横向非线性振动，利用数值法得到了准周期振动结果。姚国等[4]对大挠度薄板在横向均布载荷下的混沌运动进行研究，利用数值法得到板从周期到混沌运动的振动过程。李自刚等[5]在分析具有轴承不对中故障的柔性非圆截面多转子系统的非线性动力学问题中，利用数值法得到混沌运动与准周期运动互相交替出现的现象。侯东晓等[6]基于广义拉格朗日方程建立了含Davidenkov滞后环连续轴的相对转动动力学方程，分析了该非线性方程在自治和非自治情况下的分岔特性，观察到了周期运动、倍周期运动和准周期运动等多种运动形态。张留伟等[7]通过Lyapunov函数建立了辅助线性方程的指数型二分性，研究了广义非线性Duffing方程准周期解的存在性。丁虎等[8]通过不同截断阶数Galerkin方法，利用四阶龙格库塔法求解了轴向加速黏弹性梁系统的控制方程，识别了系统中存在的准周期运动形态。伍新等[9]发展了传统的反控制方法，并基于此方法研究了一类三自由度含间隙碰撞振动系统的分岔反控制问题，分析了该系统准周期分岔解的稳定性。孙军平等[10]采用准周期随机声脉冲序列船舶辐射噪声模型，获取了船舶水下辐射噪声功率谱的特征。李小彭等[11]建立了多自由度内共振系统动力学方程，通过数值计算，观察到工件-刀架子系统的准周期运动和混沌运动现象。

在众多学者研究中，主要是利用数值法发现并分析准周期运动，然而数值法不能很好地提供准周期解的全貌，无法了解其运动的机理。因此，有必要在准周期运动的近似解析分析方法上做进一步的研究。IHB法由Lau等[12]在1981年首先提出，其本质就是将增量法和谐波平衡法相结合，是一种半数值半解析求解非线性振动问题的方法，可获得非线性系统高精度高阶谐波解[13]。该方法不但适合于弱非线性系统，而且适合于强非线性系统，所以在工程上得到了广泛的应用[14]。Lau等[15]首先采用多时间尺度增量谐波平衡法分析了简支梁自由振动内共振引起的准周期问题。近年来，诸多学者利用该方法进行了大量振动问题的研究，并取得丰硕成果。黄建亮等[16]利用增量谐波平衡法研究了轴向运动梁在不同轴向速度下的非线性振动，并讨论了内部出现共振时的临界速度。Xu等[17]利用增量谐波平衡法研究了含有子系统的运动梁在时变作用下的非线性振动，分析了高维非线性系统模型下稳态解的收敛性。Wang等[18]利用增量谐波平衡法分析了双级功率因数校正变换器的周期振动。李应刚等[19]研究了外部动态激励作用下齿轮系统的非线性动力学特性，采用增量谐波平衡法求解了齿轮系统的稳态周期响应。唐元璋等[20]将增量谐波平衡法运用到分析Duffing振子倍周期分岔规律的研究中，获得了高精度高阶谐波半数值近似解析解。Huang等[21]分析了受简谐激励作用的弯曲梁在含有二次、三次非线性项时的非线性振动，得到了内共振条件下的周期解、准周期解及混沌现象。然而，以往的研究中很少涉及利用增量谐波平衡法解决非线性系统准周期运动的问题。

本文提出将IHB法与多时间尺度相结合，分析非线性系统的准周期运动。结果表明，结合多时间尺度的IHB法是求解非线性振动方程的一种有效方法，将该方法的应用范围从周期运动扩展到准周期运动。

1 方法推导

本文应用IHB法研究非线性系统的准周期振动，现以下面的典型单自由度Duffing型非线性振动方程为例，说明IHB法的求解过程。

(1)

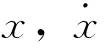
τi=ηωit(i=1,2,3,…,ms)

(2)

(3)

其中，η为有理数，并且在时间域上，有

0≤τi≤2π

(4)

无论选取什么样子的时间尺度，外激励的频率都可以选取如下的时间尺度来表示：

(5)

其中

(6)

将式(5)和(6)代入式(1)得

(7)

x=x0+Δx,ωi=ωi0+Δωi

(8)

把式(8)代入式(7)，整理并略去高阶小量，得线性化增量方程

(9)

IHB法的第二步是谐波平衡过程，准周期解用矩阵形式可表示为

x=Ta

(10)

其中，T=[Tc,Ts]为谐波项，a=[ac,as]T为谐波项系数。谐波项中余弦项数目为Nc，正弦项数目为Ns，那么对于单自由度系统其谐波项的数目总共为

N=Nc+Ns

(11)

将Δx=T·Δa代入式(11)得

(12)

将式(12)经Galerkin过程，可得到如下方程

(13)

其中

(14)

KT为N×N的切向刚度矩阵，包含线性部分与非线性部分

Δa=Δac+Δas

(15)

F-H·a

(16)

R称为残余向量，当x0与ωi0为准确解时，有R=0。F为与外激励相关的向量，H为总体刚度矩阵，R的值受F与H的影响，其值分别为

dτ1dτ2…dτms

(17)

dτ1dτ2…dτms

(18)

ΔF为增量力，即

(19)

(20)

KTΔa=R

(21)

方程(21)是一个不定方程，求解该方程时，先指定初值a和ωi，求得Δa。之后，以a+Δa代替原来的a，代入式得到新的Δa。重复迭代计算，直到修正值满足收敛准则的要求。于是，就可以得到方程组的解。

2 算例结果与分析

2.1 Duffing方程算例

含三次非线性项的Duffing系统在受到两个外激励作用时，振动微分方程可写为：

(22)

系统运动解的表达式为

q(t)=a1cosτ1+a2cosτ2+a3cos(2τ2-τ1)+

a4cos(3τ2-2τ1)+a5cos(4τ2-3τ1)+b1sinτ1+

b2sinτ2+b3sin(2τ2-τ1)+b4sin(3τ2-2τ1)+

b5sin(4τ2-3τ1)

(23)

经IHB法运算后，各频率分量与其对应的谐波项系数如表1所示。

表1 Duffing方程相应谐波项系数值Table 1 Corresponding harmonic coefficient values of Duffing equation

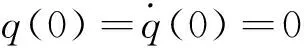
图2是用IHB法得到的系统频谱图，并用R-K4法与其进行对比。事实上，系统频率的组合形式是多种多样的，为方便研究，选取几种重要的频率组合。从整体上看，图2中由IHB法和数值法得到的占据主导地位的频率分量及其谱值是相同的。系统频率ω在1.0(ω1)处的谱值最大，在3.141 592 6(ω2)处的谱值次之，其频率值正好等于两个外激励的频率，说明该两频率响应在系统的响应中占据主导地位。其次，频谱图呈现出“簇状峰”模式，谱线的位置不随时间变动，说明系统的运动形式是准周期运动。

图1 当两个外激励频率时的系统时间历程图Fig.1 System’s time history diagram as

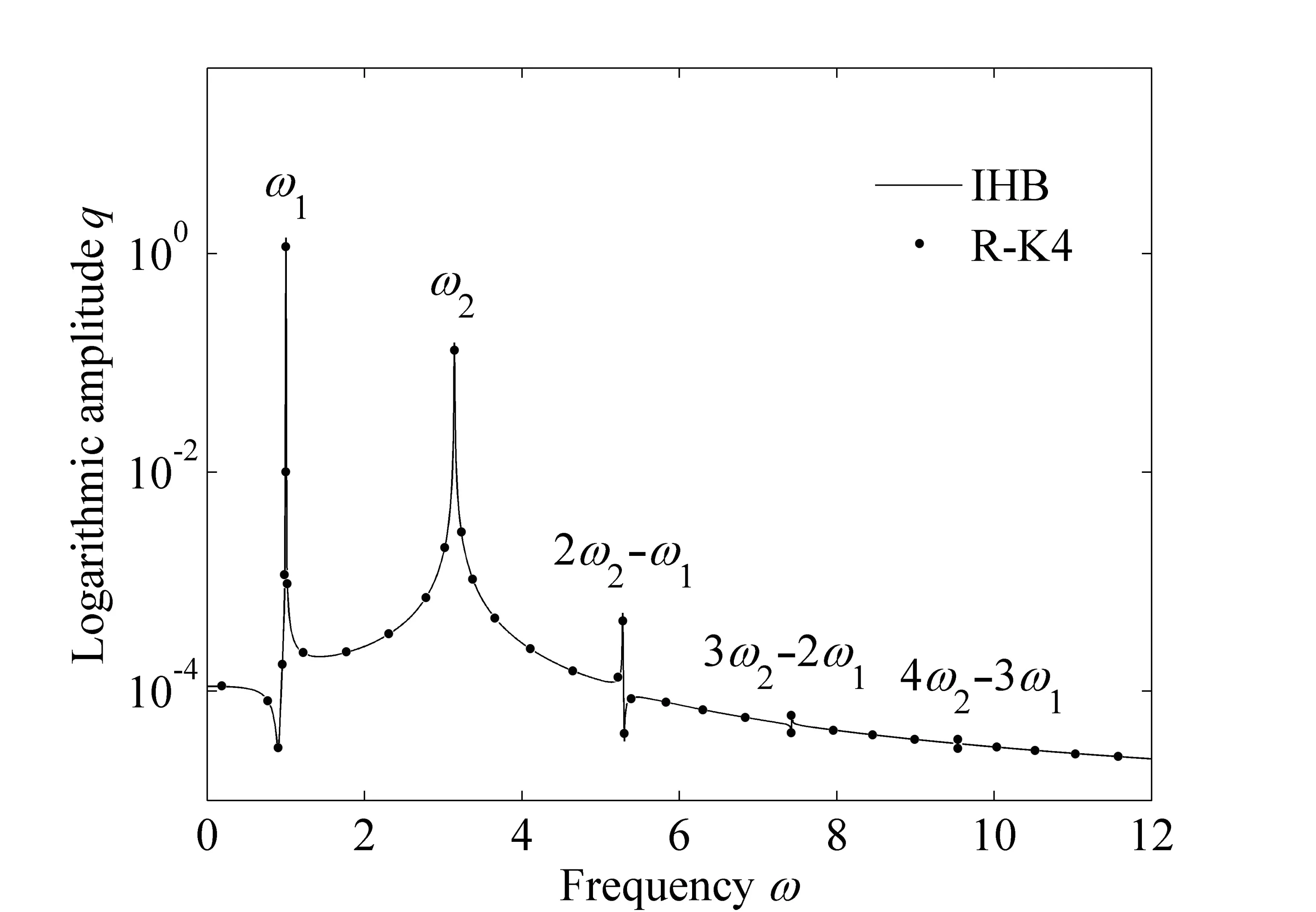
图2 当两个外激励频率时的系统频谱图Fig.2 System’s spectrum diagram as

图3为用IHB法做出的系统相平面图，该图显示系统的相轨迹总是保持在有限的范围内，排布密集但没重叠，相互交叉却不封闭，而周期振动的相平面图中只含一条简单闭合曲线，亦说明了系统的运动形式是准周期运动。

事实上，系统频率的组合形式是多种多样的，为方便研究，选取几种重要的频率组合。从整体上看，图2中由IHB法和数值法得到的占据主导地位的频率分量及其谱值是相同的。系统频率ω在1.0(ω1)处的谱值最大，在3.1415926(ω2)处的谱值次之，其频率值正好等于两个外激励的频率，说明该两频率响应在系统的响应中占据主导地位。其次，频谱图呈现出“簇状峰”模式，谱线的位置不随时间变动，说明系统的运动形式是准周期运动。

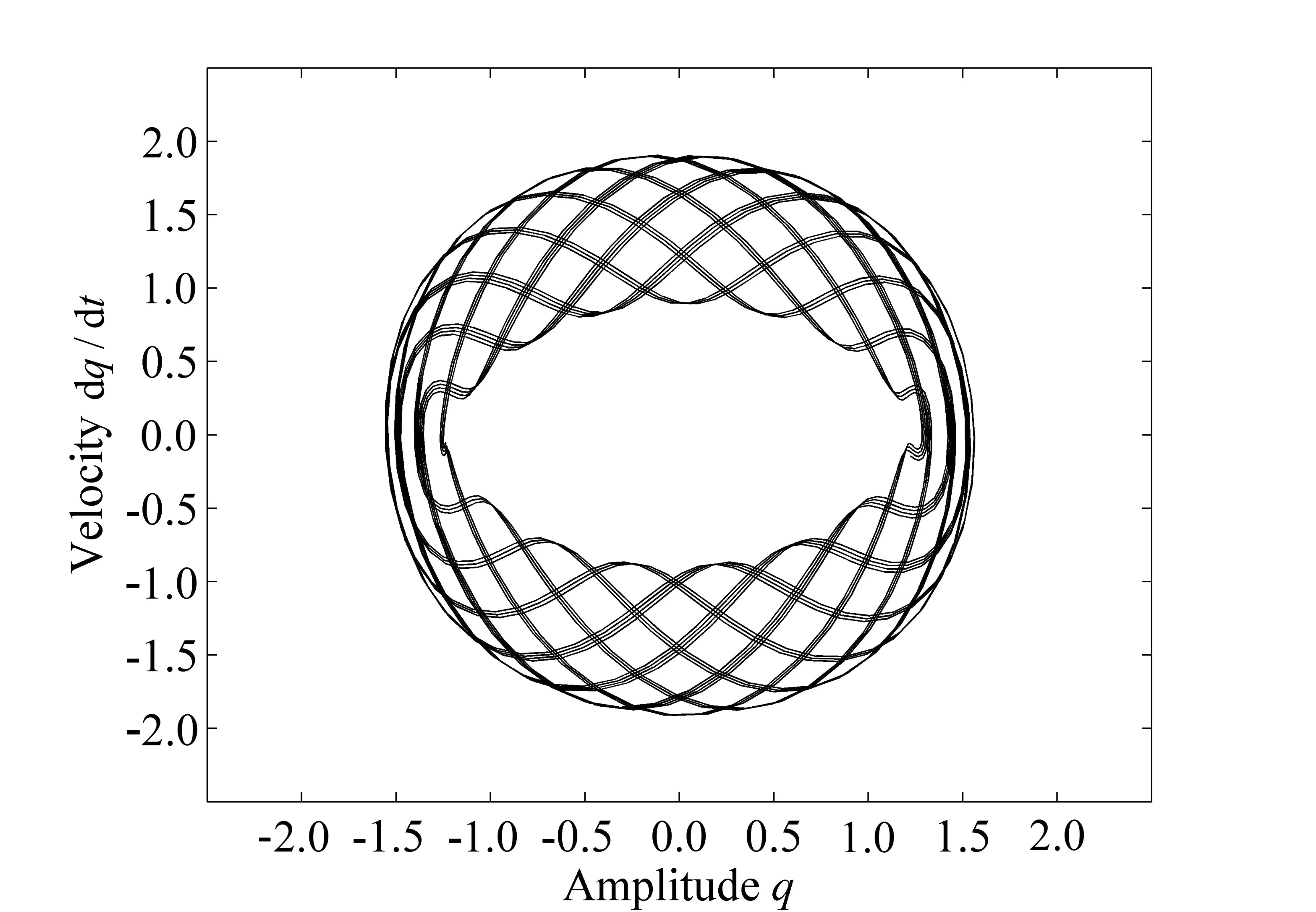
图3 当两个外激励频率时的系统相平面图Fig.3 System’s phase diagram as

如图4所示，由R-K4法得到的Poincaré图中的相点整齐地排布在一封闭的曲线上，而周期振动的Poincaré图中只有一个相点，从动力学特性可知其所做的运动为准周期运动。

图4 当两个外激励频率时的系统Poincaré图Fig.4 System’s Poincaré section as

2.2 van der Pol-Duffing方程算例

含三次非线性项的van der Pol-Duffing系统受到两个外激励作用时，振动微分方程为

p1cos(ω1t)+p2cos(ω2t)

(24)

q(t)=a1cosτ1+a2cosτ2+a3cos(τ1-2τ2)+

a4cos(2τ1-τ2)+b1sinτ1+b2sinτ2+

b3sin(τ1-2τ2)+b4sin(2τ1-τ2)

(25)

用IHB法求得的各频率分量与其对应的谐波项系数如表2所示。

表2 van der Pol-Duffing方程相应谐波项系数值Table 2 Corresponding harmonic coefficients values of van der Pol-Duffing equation

图5 当两个外激励频率时的系统时间历程图 Fig.5 System’s time history diagram as

图6是用IHB法做出的系统频谱图，并用R-K4法与其进行对比。类似地，只取几种重要的频率组合。观察图6可知，由这两种方法得到的占据主导地位的频率分量及其谱值是相同的。系统频率ω在0.756(ω2)处的谱值最大，在1.0(ω1)处的谱值次之，其频率值正好等于两个外激励的频率，说明该两频率响应在系统的响应中占主导地位。显然，频谱图呈现出“簇状峰”模式，谱线的位置不随时间变动，说明系统的运动形式是准周期运动。

图6 当两个外激励频率时的系统频谱图Fig.6 System’s spectrum diagram as

图7是用IHB法做出的系统相平面图，与图3类似，该图显示系统的相轨迹为有界环内的往复运动，相轨迹排布密集但没重叠，相互交叉却不封闭，亦说明系统的运动形式是准周期运动。

图7 当两个外激励频率时的系统相平面图Fig.7 System’s phase diagram as

如图8所示，用R-K4法得到的Poincaré图中相点整齐地排布在一封闭的曲线上，与图4呈现相同的规律，可以推断系统做准周期运动。

图8 当两个外激励频率时的系统Poincaré图Fig.8 System’s Poincaré section as

3 结 论

用IHB法可得到含有三次非线性项的振动方程解的表达式，适用于非线性系统的准周期求解。该法将求解非线性振动微分方程转化为求解线性代数方程组的问题，具有迭代次数少，收敛快，精确度高等优点。

本文选取具有代表性的Duffing方程与van der Pol-Duffing方程，用IHB法分别求得系统在外激励频率不可公约时的时间历程图、频谱图、相平面图和Poincaré图。结果显示，当外激励频率不可公约时，系统将做准周期运动，其结果与数值法的结果相一致。

IHB法是一种研究非线性振动的半数值半解析方法，利用该方法可以研究较复杂非线性系统的准周期运动，对工程中广泛存在的运动系统的动力学行为的分析与控制具有重要的理论意义和应用价值。利用IHB法研究多自由度系统的准周期运动问题将是下一步的研究方向。