非线性微分方程线性化的教学改进
2018-12-04陈武晖高国琴
陈武晖, 张 军, 高国琴
(江苏大学 电气信息工程学院, 江苏 镇江 212013)
0 引言
“自动控制原理”是电气工程专业和自动化专业的核心课程,课程内容主要分为系统建模、系统分析和系统设计三大模块。其中系统建模是基础,系统分析的核心是稳定性,而系统设计是在稳定性的基础上根据性能指标进行系统综合[1]。
“自动控制原理”课程的特点是数学推导复杂、概念繁多、内容抽象,是一门公认的学生难学、教师难教的课程[2]。
目前,“自动控制原理”课程存在将其当做一门数学课程来讲的误区。教师注重理论推导以及讲解如何求解各种类型题目,这导致学生理解概念困难,难以把该课程与后续的专业课程相联系,出现理论和实践严重脱节的问题。
例如:现有的教材在控制系统数学模型一节中,对传递函数进行了详细的推导和阐述,让学生建立起模型的概念。但是对非线性微分方程线性化这一知识点却写得很简单,只给出一般的概念和推导,导致问题分析不深入,与实际应用有较大差距。
实际上,工程中大部分系统都是具有非线性的,而非线性微分方程线性化是简化模型的一项关键技术,有着明确的应用背景,后续的电类专业课程中都有相关的内容涉及。从目前讲课效果来看,学生对这部分内容理解不深入,无法将系统分析理论与实际工程对象联系起来,造成解决复杂工程问题的能力较弱。
针对上述情况,结合我院电气工程专业和自动化专业的具体情况,对这部分教学内容进行改进,在原有的一般理论推导过程中,分别针对电气工程专业和自动化专业增加了风力发电的小扰动线性化建模和飞行器的小扰动线性化动力学建模两个知识点,让学生对该部分教学内容理解和应用有了更加深入的认识,从而取得了良好的课堂效果。
1 风力发电的小扰动线性化建模
风力发电是电气工程领域中的新兴技术,是把风能转换成机械能,再把机械能转化为电能的过程。
风力发电具有明显的随机性、波动性、间歇性等特点,大规模风电场接入电网,会改变电力系统原有的结构和运转方式,势必会给电力系统的小扰动稳定性造成一定影响,这是一个非线性问题。因此,需要研究风力发电的小扰动线性化数学模型。我们根据专业特色将任课教师的“含大规模风电场的电力系统分析”科研成果移植到这部分教学中[3]。通过这种根据实际应用的需求将风力发电专业的背景阐述出来的教学方式,极大增强了学生学习“自动控制原理”的兴趣。
我们在授课中遵循“基础性知识→专业性综合知识→系统性创新知识”的多层次培养原则,通过多媒体课件PPT和板书结合的方法多角度展现这一知识点的不同层面内涵。在阐述应用背景之后,风电机组的电力系统机电暂态特性的分析便可以描述为微分—代数方程组。其中用非线性一阶常微分方程来表述元件的动态特性,用非线性代数方程(组)表示传输网络的准稳态行为,其表达式如下:
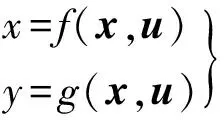
(1)
式中,x为方程组中系统状态变量,u为输入向量,y为输出控制向量。将式(1)在稳态运行点(x0,u0)线性化可得:
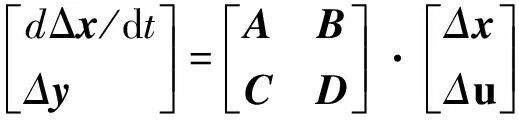
(2)
式中:
Δx是n维状态向量;Δu是r维输入向量;Δy是m维输出向量;A是n×n状态矩阵;B是n×r控制矩阵;C是m×n输出矩阵;D是m×r前馈矩阵。这样,在讲述非线性系统概念时便有了明确的物理对象,即电力系统的暂态动态行为是非线性的。在讲述公式(2)的含义和推导过程中,很自然地与传统教材中的非线性微分方程线性化的知识点相对应,即
Δy=xKΔx
(3)
公式(2)是公式(3)的维数推广矩阵,系统工作点的概念与电力系统稳态运行点(x0,u0)相对应,这样原有的抽象空洞的概念有了明确对象,理解便容易,并且这种方式讲述把专业的知识串联起来,系统性很强,还原了“自动控制原理”课程的本色。
在此基础上,设此时系统的稳态平衡点(x0,u0)不是网络方程的奇点,对式(2)进行Laplace变换之后可得
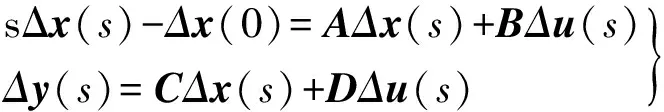
(4)
对式(4)化简之后可得Δx在频域范围内的表达式:
Δx(s)=(sI-A)-1[Δx(0)+BΔu(s)]
(5)
通过上述讲述,学生初步建立了电力控制系统的数学概念,加深了其与实际对象的联系,在后续的专业课中会自然而然地联系到“自动控制原理”的知识点,巩固了相应的建模基础。
2 飞行器小扰动的线性化动力学建模
对于自动化专业的学生,四轴旋翼飞行器是大学生创新比赛的常见对象之一。通过四轴旋翼飞行器的小扰动线性化建模,可以明显提高学生学习“自动控制原理”的热情,理解控制的本质。
四轴旋翼飞行器在空间的运动可以描述为一组非线性微分方程组,代表了飞行器空间运动的物理本质,主要包括运动学和动力学两部分模型,其中运动学方程为
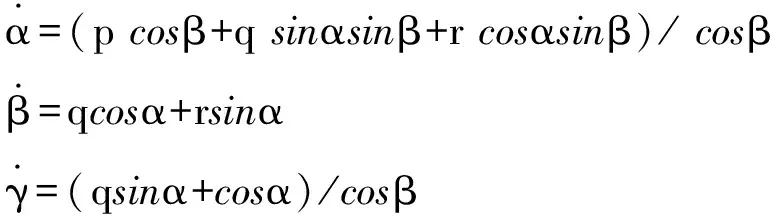
(6)
式中α、β、γ三者分别是横滚角、俯仰角、偏航角;p、q、r是ω在机载坐标系中X轴、Y轴、Z轴上的分量。其中动力学方程为
(7)
式中Mz、My、Mz是机体上力矩M在机载坐标轴上的分量,Ix、Iy、Iz是惯量I在机载坐标轴的分量。针对公式(6~7)通过课堂讨论方式,能详细了解四轴旋翼飞行器的俯仰、偏航、滚动通道存在的非线性耦合、惯性耦合、控制耦合等概念,与前面讲过的线性叠加定理相对应。由此,学生明确建立了非线性系统概念,与原来简单空洞地阐述非线性系统f=f(x)概念有着本质的区别。
在非线性概念的基础上,假设飞行器运动参数与在同一时间内未扰动参数数值间的差异很小,对飞行器非线性模型在平衡点处实施小扰动,然后将非线性模型展开为Taylor级数,忽略高次项,得到近似的线性模型,即
(8)
我们在课堂上分析航空航天中的这种小扰动动力学建模是一种小偏差线性化方法,前提是假设输入量和输出量在静态工作点附近作微小变化,这与“自动控制原理”的非线性微分方程线性化的理论适用场合完全对应,这样将两门课程有机地联系起来,培养了学生分析问题的能力[4]。在此基础上,用小扰动线性化方法处理式(6~7),通过Matlab课堂教学软件现场得到俯仰通道传递函数为
(9)
通过这样有明确应用背景的阐述,使自动化专业学生初步建立飞行器非线性系统概念,以及如何线性化建模,为后续的PID控制律设计打下基础。此后,可进一步分析阐述线性化模型的适用范围。当飞行器姿态角与工作平衡点的范围小于10°时,线性化误差很小,因此工程上采用线性化小扰动模型作为常规飞行器的控制设计模型是合宜的。当与工作平衡点的范围大于10°时,飞行器运动学方程中的Δe=sinα-α线性化误差明显加大(见图1),线性模型不能完全反映飞行器的动态特性,需要采用非线性模型,这也是当今高超声速飞行器新的的制导和控制方向研究重点,从而进一步拓展学生的知识视野[5]。
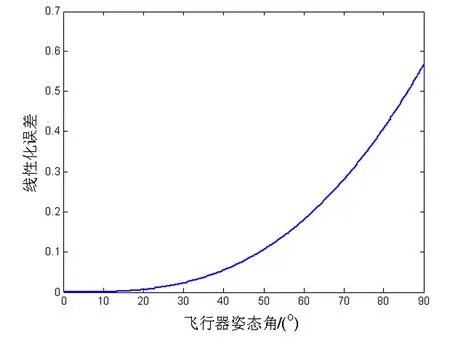
图1 飞行器姿态角线性化误差变化图
该教学改进已在我院的自动化专业2013级03班学生中进行试验,并且在2015年学生评教中获得我院的最高分,学生认为这种有明确应用背景的知识讲解,把自动化专业的特色鲜明凸现出来,有利于提高设计复杂工程的能力。
3 结语
我们在“自动控制原理”非线性微分方程线性化的这一章节的教学改进中,对电气工程专业的学生授课时,增加了大规模风电场的电力系统小扰动线性化建模实例;对自动化专业学生的授课时,增加了四轴旋翼飞行器的小扰动线性化建模实例,使得线性化建模知识点与工程实践有机结合起来,有效提高学生解决复杂工程问题的能力。
