破解含有量词的问题

2018-12-04张荣彬

新世纪智能(数学备考) 2018年10期

关键词：值域量词水运

张荣彬

若M是给定的集合，p（x）是一个含有x的语句，那么称“∀x∈M，p（x）”为全称命题，称“∃x∈M，p（x）”为存在性命题．用这种逻辑用语来表达的数学问题具有简捷、新颖、抽象的特点．以下将此类问题的解法要点作简要的归纳梳理．

一、例题精选

例1已知f（x）是定义在R上的奇函数，且对任意x1≠x2均有成立．

（1）若对 ∀x∈［0，1］，f（t·9x－1）＋f（3x＋2）＜0成立，求实数t的取值范围；

（2）若 ∃x∈［0，1］，使f（t·9x－1）＋f（3x＋2）＜0，求实数t的取值范围；

（3）若 ∃x∈［0，1］，使f（t·9x－1）＋f（3x＋2）＝0，求实数t的取值范围．

例2已知函数f（x）＝ax－lnx（a∈R）．若对 ∀x∈ ［1，＋ ∞）均有f（x）≥成立，求实数a的取值范围．

例3已知

（1）若对 ∀x2∈ ［0，2］，∃x1∈ ［0，2］，使得f（x1）＞g（x2），求实数a的取值范围；

（2）若对 ∀x2∈ ［0，2］，∃x1∈ ［0，2］，使得f（x1）＝g（x2），求实数a的取值范围；

（3）若 ∃x1，x2∈ ［0，2］，使得f（x1）＞g（x2），求实数a的取值范围．

二、解题分析

例1的解析

由已知得f（x）是奇函数也是R上的增函数，观察3个小问后，不妨设，因为x∈［0，1］，可求出g（x）的值域是于是本题的3个小问可分别翻译为：

t＜g（x）恒成立、t＜g（x）有解和t＝g（x）有解，从而t＜g（x）min＝－2、和

例2的解析

此时想起老师的告诫：解决恒成立问题，首选的方法是分离变量，若不能分离或分离后不易求出所要的结果，可以考虑带参讨论或数形结合．

当a＝0时，h（x）＝－2lnx≤0，不合题意；

当a≥1时，方程ax2－2x＋a＝0的判别式Δ＝4－4a2≤0，h′（x）≥0，所以h（x）在x∈［1，＋∞）时单调增，此时h（x）min＝h（1）＝0，适合题意；

当a≤－1或a∈（－1，0）时，h（x）在x∈［1，＋∞）时单减，此时h（x）max＝h（1）＝0，不合题意；

当a∈（0，1）时，方程ax2－2x＋a＝0有2个不等正数根x1，x2，因为x1x2＝1，若设x1＜1＜x2，则h（x）在［1，x2］上单调减，在（x2，＋∞）上单调增．因h（1）＝0，所以h（x）≥0不能恒成立．

综上知，a≥1为所求．

例3的解析

f（x）在［0，2］上的值域是［0，4］，g（x）在［0，2］上的值域是［－a，ln3－a］．

（1）对 ∀x2∈ ［0，2］，若 ∃x1∈［0，2］，使得f（x1）＞g（x2），即f（x）max＞g（x）max，须有4＞ln3－a，所以a＞－4＋ln3．

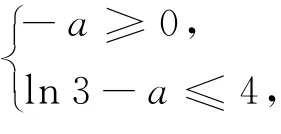
2017年4月，交通运输部联合广东、广西、贵州、云南4省区人民政府联合印发《珠江水运科学发展行动计划（2016—2020年）》（以下简称《行动计划》）。5 月，交通运输部印发《珠江水运发展规划纲要》（以下简称《规划纲要》）。同年，珠江实现了亿吨水网、亿吨干线、亿吨港口、亿吨船闸“四个亿吨”目标，珠江水运的发展迈上了新的量级。今年，《推进珠江水运绿色发展行动方案（2018—2020年）》（以下简称“ 绿色行动方案”），由交通运输部联合广东、广西、贵州、云南4省区人民政府印发，吹响了珠江水运走生态优先、绿色发展之路的号角……

（3）若 ∃x1，x2∈ ［0，2］，使得f（x1）＞g（x2），则f（x）max＞g（x）min，即4＞－a，所以a＞－4．

三、方法总结

1．翻译转化量词

当题中只有一个量词时，通常可转化为以下的2个基本事实：

（1）∀x∈M，t＜f（x）⇒t＜f（x）恒成立 ⇒t＜f（x）min；

（2）∃x∈M，t＜f（x）⇒t＜f（x）有解 ⇒t＜f（x）max；

∃x∈M，t＝f（x）⇒t＝f（x）有解⇒t∈f（x）的值域．

当题中含有两个量词时，去化量词的情况较为复杂，为防死记硬背，这里以例3为例介绍2种方法：

二是搭桥法：∀x2∈ ［0，2］，∃x1∈［0，2］，使得f（x1）＞g（x2）⇔∀x2∈ ［0，2］，∃x1∈［0，2］，使得f（x1）＞M＞g（x2），而 “∀x2∈ ［0，2］，M＞g（x2）⇔M＞g（x）max”，“∃x1∈ ［0，2］，f（x1）＞M⇔f（x）max＞M”，于是得f（x）max＞g（x）max．本例的（2）与（3）可用同样的方法完成．