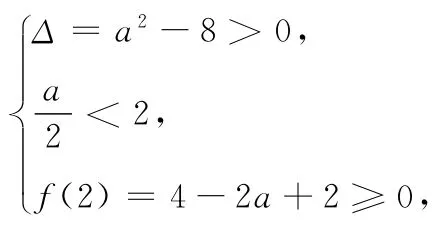老师，我怎么学会思考——函数与性质篇

王思俭

函数是高中数学的重要内容，也是高考必考的知识点，难度通常处于中档偏上，但考生通常会问：

老师，我就是不理解函数迭代，对于f（f（x））类问题屡做屡错，怎么办？

分界点不确定的分段函数题如何思考？这个条件怎么使用？这类函数图象该怎么画？

含绝对值的函数问题怎么这么难？

为此，我邀请几位同学就“函数与性质篇”进行交流，旨在引导学生深刻理解函数概念，灵活运用函数性质，启迪他们的数学思维．

第（1）小题会做，利用分类讨论思想，不等式f（x）＜0的解集是（1，4）．但第（2）小题两个函数的分界点是可变的，我不知道怎样去画图，该怎么做呢？

教师：对于分界点不确定的分段函数，你们可以先作出两段函数的图象，然后移动分界点，找出适合本题的答案，要学会用运动的观点思考数学问题．

生甲：先作出函数y＝x－4与y＝x2－4x＋3的图象，求出前者有一个零点4，后者有两个零点1和3，再由数形结合得，当λ＞4时，函数f（x）恰有2个零点．

图1

生乙：答案不全，当1＜λ≤3也符合要求．其实本题可以继续探究：当3＜λ≤4时，f（x）恰有3个零点；当λ≤1时，f（x）恰有1个零点．

教师：很好！生乙研究其他零点的情况，探究性学习是学会数学思考的一个重要环节．你们可以发现吗？函数y＝x－4与y＝x2－4x＋3没有交点，如果有交点，情况如何？请看变题：

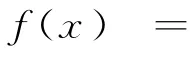
生甲：利用数形结合思想求解，函数y＝x＋1有一个零点－1，y＝x2－4x＋3有两个零点1和3，作图可得，－1≤λ＜1．

教师：正确！本题容易遗漏左端点－1．如将问题改为：

若存在实数c使得函数g（x）＝f（x）－c有3个零点，则λ的取值范围是________．

本题是存在实数c，你们怎么去思考？又如何求解？

生甲：这题有c和λ两个参数，不知道移动哪一个参数？

教师：由于是存在实数c，作出两段函数图象，先移动y＝c，看看在何处时，它与两个函数图象有三个交点，然后再移动分界点x＝λ，这样思考是否可以求出来了？

生丙：因为f（2）＝f（－2）＝－1，要使g（x）＝f（x）－c有3个零点，等价于y＝f（x）与y＝c必有3个不同交点，结合图象知，－2＜λ＜1．

教师：很好！原题和变题中的分段函数的分界点是参变量，每段函数都是确定的，也可以改为，某一段函数解析式中含有参数，再研究相关问题．请看变题：

生丁：类似上述变题，一次函数在x＝0处的函数值为a，二次函数在x＝0处的函数值为3，问题转化为函数y＝f（x）与y＝2a－1必有3个不同交点，结合图象知，－1＜2a－1＜a，即0＜a＜1．

教师：很好！还是从动态观点出发寻找解题的突破口．当然如果分段函数中两个函数都含有参数，又可以改编为一道新的题目（参见实战演练3）．

生乙：已知函数f（x）＝x2＋（2a＋1）x＋a2，若f（f（x））≥0恒成立，求实数a的取值范围．

如果把f（f（x））整理成四次函数，根本无法求解．

教师：这是函数迭代问题，它的含义是对应法则f再一次对函数值f（x）作用后，输出的结果是f（f（x）），这时我们可以将f（x）看成整体t，问题转化为f（t）≥0在一定范围内恒成立．

生甲：令t＝f（x），不等式转化为t2＋（2a＋1）t＋a2≥0恒成立，于是判别式Δ≤0，求得

生戊：不对！还应该考虑t的取值范围，t的范围就是函数f（x）的值域，即因此问题等价转化为t2＋（2a＋1）t＋a2≥0在恒成立．首先考虑判别式Δ≤0；其次考虑Δ＞0时，对称轴的位置必须在指定区间的左侧，同时区间端点对应的函数值非负，于是就有不等式组解之得

综上所述，a的取值范围为

教师：分析到位，答案正确！

股骨头坏死的发病率逐年上升，且呈年轻化趋势，给患者日常生活带来影响。股骨头坏死发生的因素有很多，主要原因是缺血，且具有很长的潜伏期。对于此类患者来说，其发生病理改变主要有2个阶段，初阶段，由于患者细胞缺血，骨髓细胞与骨细胞会大面积死亡，从而导致股死亡；修复阶段，患者骨与血管会再生，骨小梁吸收[3-4]。因此，患者在发病初期，并不会出现明显的症状，发生症状时，已经确诊为晚期，导致患者错过了最佳治疗机会，影响其预后效果及生活质量。临床资料显示，股骨头坏死患者的治疗效果，会受到患者病情严重程度、坏死范围影响。所以，只有早日诊断疾病，才能尽早接受治疗。

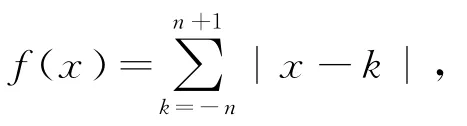
我拿到这道题一下子全蒙了，不知道如何下手，不知道从哪里考虑问题．

生丁：我就认为a2－2a＝3a－1，求出，直觉告诉我，a还应该有其他的值，但不知道怎样考虑．

教师：你可以对n先试验几个值，如n＝1，2，作出函数的图象，研究函数的对称性、单调性等，然后再将问题转化为相关的方程或不等式．

生戊：当n＝1，2时，通过对函数f（x）的研究，发现f（x）的图象关于直线对称，于是可以证明对一般情况也成立，同时当0≤x≤1时，f（x）＝（n＋1）2为常函数，因此当x≥1时，f（x）单调递增；当x≤0时，f（x）单调递减．由对称性知a2－2a＋3a－1＝1，解之得，a＝－2或a＝1．所以a的值为a＝－2或a＝1或

教师：答案虽然是对的，但过程不严谨．你们想一想，如果a2－2a，3a－1都在［0，1］内时，f（a2－2a）＝f（3a－1）是不是也成立呢？要不要考虑呢？

众生：应该考虑，但我们都疏忽了！但这种情况无解．

1．函数的性质（如定义域、函数的奇偶性、对称性、周期性和单调性等性质）是什么？

2．能否作出函数图象？怎样作出函数图象？是描点作图还是平移变换（或伸缩变换）作图？

3．题目中哪个是主元？哪个是参数？有几个参变量？利用什么策略求解？

4．本题涉及哪些知识点？运用哪几种数学思想方法？能否继续演变新的问题？

……

实战演练

3．已 知a∈ R，函数若函数f（x）恰有3个零点，则a的取值范围是________．

参考答案

1．0≤a≤2．

2．（－1，0）∪ （1，＋∞）．

详细解析：

1．因为当x≤0时，f（x）＝（x－a）2，又f（0）是f（x）的最小值，所以a≥0．

当x＞0时，f，当且仅当x＝1时取“＝”．

要满足f（0）是f（x）的最小值，需2＋a≥f（0）＝a2，即a2－a－2≤0，解之，得－1≤a≤2，

所以a的取值范围是0≤a≤2．

2．当x＜ 0 时所以f（x）为奇函数，作出函数图象如图所示，要使f（m）＞f（－m），即f（m）＞－f（m），f（m）＞0，由图象可知，m∈ （－1，0）∪（1，＋ ∞）．

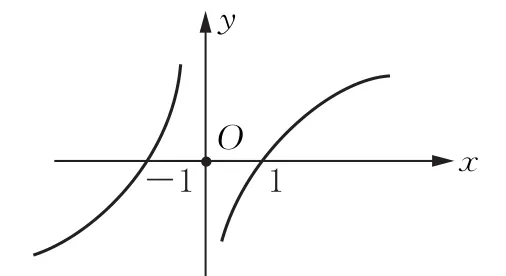
图2