基于LS-DYNA火药材料模型的二次开发
2018-12-04王飞虎姚养无
王飞虎,姚养无
(中北大学 机电工程学院,太原 030051)
枪炮的内弹道性能预算,是枪炮设计的重要内容。目前,对于内弹道解,国内外主要采用数值计算方法对内弹道过程进行数值计算和模拟。该方法首先要建立内弹道基本方程,然后根据射击过程的初始条件和内膛结构的边界条件进行数值模拟[1]。但是,对于复杂的内弹道模型,如水下内弹道、高低压内弹道、多相流内弹,其内弹道方程建模复杂,工作量比较大。
LS-DYNA是军用和民用相结合的通用结构分析非线性有限元程序,并向用户提供了二次开发平台。用户可以通过构建材料本构方程或状态方程,编写子程序,然后与LS-DYNA编译链接,生成新的求解器,该求解器拥有新的自定义材料。
在理解火药状态方程、火药燃烧规律和LS-DYNA二次开发技术基础上,根据火药的状态方程和燃烧规律,按照LS-DYNA二次开发编程规则,编写LS-DYNA子程序,与LS-DYNA编译链接,至此,生成拥有火药材料的求解器。对于复杂的内弹道模型,该方法可以通过一般的有限元仿真步骤,达到求解内弹道的目的,相对于内弹道数值计算方法更加简便。
为了验证火药材料模型建立的正确性,利用新生成的求解器对7.62 mm枪弹内弹道进行有限元仿真,将所得仿真结果与试验结果进行了对比。
1 LS_DYNA火药单元模型
对于火药气体单元,由热力学第一定律:
dU=dQ-pdV
(1)
dU=nCVdT
(2)
其中:U为火药气体单元的内能;Q为火药气体单元的热量;p为火药气体压力;V为火药气体单元体积;n为火药物质的量;CV为火药气体比热[2]。
对于火药气体单元,由理想气体状态方程:
pV=nRT
(3)
对方程式(3)两边同时对体积微分:
nRdT=Vdp+pdV
(4)
对于某个火药单元,在极短时间内,不考虑热散失能量,因此:
ΔQ=0
(5)
将方程式(2)、式(5)代入方程(1):
nCvdT=-pdV
(6)
联立方程式(4)、式(6)消除dT:
CVVdp=-(R+CV)pdV
(7)
整理方程式(7)可得火药气体单元体积模量K1:
火药气体k一般为1.20~1.25。
火药气体单元内能:
(8)
式(8)中:ψ为火药已燃百分数;ρ0为火药装填密度;T1为火药气体爆温[3-6]。
在火药压力p<600 MPa时,火药气体单元应该满足Nobel-Abel方程:
p(ω-α)=RT
(9)
ω=V-(1-ψ)ρ0/ρs/ρ0ψ
(10)
其中:ω为气体比容;α为气体余容[7]。
在有限元迭代计算时,在每个积分点将会分别更新单元的体积模量、压力和单元内能。为了得到气体压力和体积,可以联立式(8)(9)(10),得到以下方程组:
pψ=(k-1)U/Vψ
(11)
Vψ=V-(1-ψ)ρ0/ρs-αρ0ψ
(12)
(13)
方程初始常量可以通过k文件输入,火药燃烧百分数,可以通过火药几何燃烧模型方程求出。
由火药形状函数和火药燃速方程:
ψ=χ(1+λZ+μZ2)
(14)
(15)
其中:Z为火药已燃相对厚度;χ、λ为火药形状特征量;t为时间;p为火药气体压力;u1为燃速常数;e1为火药1/2厚度[8-12]。
2 求解器生成
对于用户自定义状态方程的二次开发,LSTC公司提供3个文件:LS-DYNA.F(主程序接口及用户自定义本构程序)、LS-DYNA.LIB(静态连接库文件)、LS-DYNA.DSP(DIGITAL VISUAL FOR—TRAN 6.0 WORKSPACE 文件)。
LS-DYNA.F文件包含LS-DYNA主程序的接口和用户自定义本构子程序,在DIGITAL VISUAL FORTRAN 6.0环境中打开LS-DYNA.DSP文件,然后打开LS-DYNA.F,编译LS-DYNA.F文件,连接静态连接库文件(LS-DYNA.LIB),生成一个用户自定义状态方程的LS-DYNA求解器,然后可以用这个求解器求解问题,在LS-DYNA的K文件中定义调用子程序关键字*EOS_UESR_DFINE。LS-DYNA在对材料单元进行积分求解时,会两次调用本构程序。当iflag等于零时,程序会更新状态体积模量;当iflag等于1,程序将会更新压力和单元内能。
LS-DYNA.F文件主体内容如下:

3 7.62 mm内弹道模型
7.62 mm内弹道试验参数如表1所示,装药参数如表2所示,为了减少计算量,可构建二维内弹道模型,如图1所示,网格划分后模型如图2所示,并对内弹道进行以下简化:不考虑内弹道挤进过程,用挤进启动压力代替,大小设为30 MPa,通过点火压控制;通过计算次要功系数,调整弹丸质量,来模拟次要功对内弹道的影响,如表3所示。材料参数关键字输入卡片如表4所示。

表1 7.62 mm普通弹试验参数

表2 2/1樟火药参数

表3 次要功系数
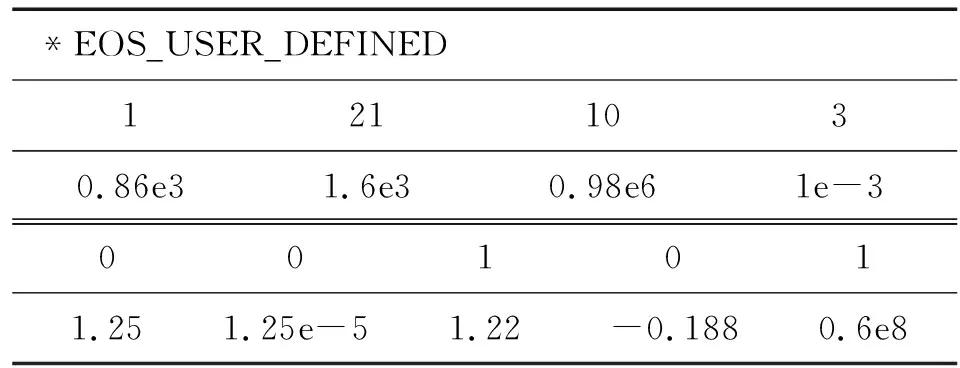
表4 火药材料状态方程card卡片参数
4 有限元分析结果
通过软件的后处理,查看内弹道各个时刻的速度云图,如图3所示。通过观察可知弹后火药气体速度呈经线性分布。
通过观察图4膛底气体时间-压力曲线,可知仿真得到的膛压符合内弹道膛底压力走势,并且,在弹丸挤进膛线0.18 ms后,膛底气体压力达到最大膛压288 MPa,与试验膛底最大膛压相差3%。
通过观察图5弹丸时间-位移曲线,可以根据身管长度确定弹丸出枪口时间。然后,通过图6弹丸时间-速度曲线,确定弹丸枪口初速。由步枪枪管在600 mm左右,可知弹丸出枪口时间在1.2 ms左右。
由出枪口时间1.2 ms,由图6弹丸时间-速度曲线,可知弹丸枪口初速为738 m/s,与试验数据误差2%。
5 结论
本文通过LS-DYNA二次开发平台,开发火药材料模型,生成能够求解火药燃烧的LS-DYNA求解器,并利用求解器对7.62 mm枪弹内弹道进行仿真计算。有限仿真得到的膛底最大膛压、枪口初速与试验结果误差在3%范围内。由以上可得出以下结论:建立的火药材料模型比较准确,能够简少了内弹道数值建模的工作量,对于内弹道求解过程一般化、程序化有一定的作用。
