求一类椭圆面积的多种方法
2018-12-03刘春辉
刘春辉
(赤峰学院 数学与统计学院,内蒙古 赤峰 024001)
1 引言
椭圆作为一类重要的平面二次曲线,不仅是平面解析几何的重要研究对象之一,而且也是高等数学[1]课程各个知识模块经常提及的话题.图形面积求取问题是贯穿于数学学习和研究过程的一个基本问题,贯穿于初等数学和高等数学的始终,其中蕴含着大量的数学方法和思维技巧.就同一类问题而言,如果从多角度多侧面进行分析,不但可以得到多种不同的解决问题的方法,而且也有助于培养学生综合运用知识的思维能力和创新能力.
鉴于此,本文针对如下一类椭圆面积的求解问题,从多个角度进行分析和思考,获得了该问题的多种解决方法.文中涉及的数学基本知识全部取自[1-4],这里不再一一赘述.
2 问题的提出
3 问题的多种解决方法
显然,解决问题的关键在于求出椭圆长半轴和短半轴之积!
方法一利用一元函数极值法求椭圆面积
假设直线 y=kx 与椭圆 ax2+bxy+cy2=1(a>0,c>0 且4ac-b2>0)分别相交于点 A(x1,kx1)和 B(x2,kx2),则 A 与 B 两点间距离为

将y=kx代入椭圆方程ax2+bxy+cy2=1,整理得

解得

因此
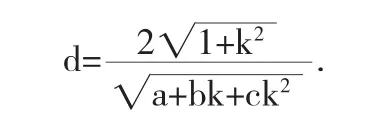
对任意的k∈R,构造关于k的函数

令f'(k)=0,即bk2+2(a-c)k-b=0,解之得f(k)的两个极值点k1和k2,于是由f'(ki)=0,i=1,2便得f(k)的两个极值

因此,椭圆面积为


方法二利用一元二次方程的判别式法求椭圆面积
类似于方法一,假设直线y=kx与椭圆ax2+bxy+cy2=1(a>0,c>0 且 4ac-b2>0)分别相交于点 A(x1,kx1)和 B(x2,kx2),且则A与B两点间距离为d,则对任意的k∈R,构造关于k的函数
若σ(k)在k点不取得极值,则根据椭圆的对称性可知,必存在两个不等的k值取得相同的函数值σ(k);若σ(k)在k点取得极值,则k必为那个唯一取到该值的点,此时记σ=σ(k)将函数变形为关于k的方程

则必有其根的判别式 Δ=0,即(bσ)2-4(cσ-1)(aσ-1)=0,整理得

这是一个关于σ的一元二次方程,其两个根σ1和σ2就是函数σ(k)两个极值,从而得即为所论椭圆的长半轴和短半轴.因此,由根与系数的关系便得椭圆面积为

方法三利用二元函数条件极值法求椭圆面积
假设椭圆 ax2+bxy+cy2=1(a>0,c>0 且 4ac-b2>0)上的点A(x,y)到坐标原点的距离为d,则可得d关于变量x和y的二元函数关系

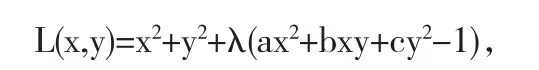
求其对变量x和y的偏导数,并使之为零,得方程组

因为点A(x,y)≠O(0,0),所以方程组有非零解,从而系数行列式D=0,即

整理得

这是关于λ的一元二次方程,设其二根为λ1和λ2,则因为 a>0,c>0 且 4ac-b2>0,所以 λ1+λ2<0 且 λ1λ2>0,故 λ1<0 且 λ2<0.又因为

所以x2+y2+λ=0,故可取于是便得
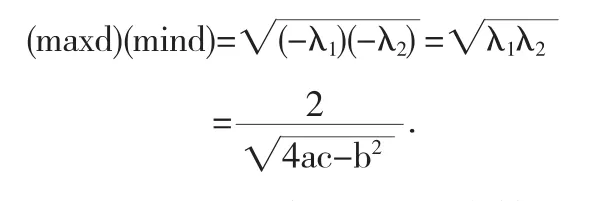
注意到maxd和mind分别为椭圆长半轴和短半轴,因此便得椭圆面积为

方法四利用直角坐标系下定积分求椭圆面积
将椭圆方程ax2+bxy+cy2=1变形得

对变量y配方得

整理得

令y+=y-得曲线y=y+(x)和y=y-(x)的两个交点的和坐标为
于是,由直角坐标系下定积分求面积公式得,椭圆面积为


方法五利用极标系下定积分求椭圆面积
任取椭圆ax2+bxy+cy2=1上一点A,设其在直角坐标系和极坐标系下的坐标分别为(x,y)和(ρ,θ),则 x=ρcosθ,y=ρsinθ,0≤θ≤2π,将其代入椭圆方程得椭圆的极坐标方程为
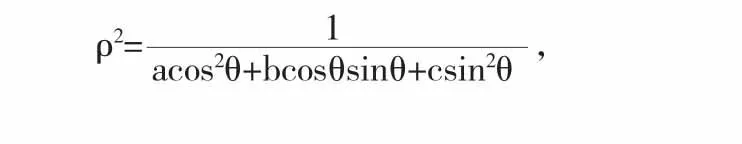
于是,由及坐标系下定积分求面积公式得,椭圆面积为

又因为

所以

方法六利用二重积分求椭圆面积
将椭圆方程ax2+bxy+cy2=1变形、对变量x配方整理得
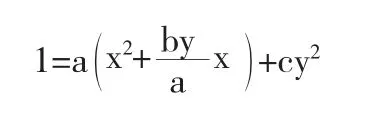

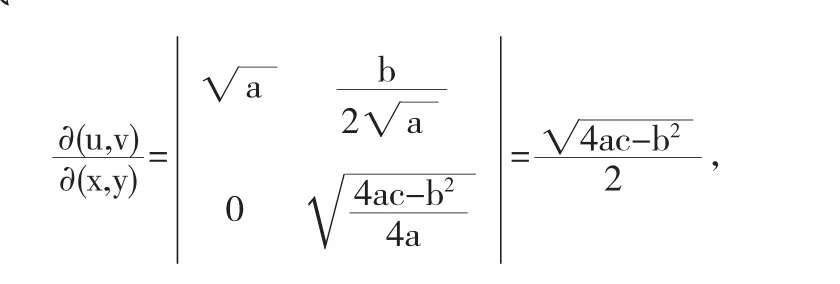
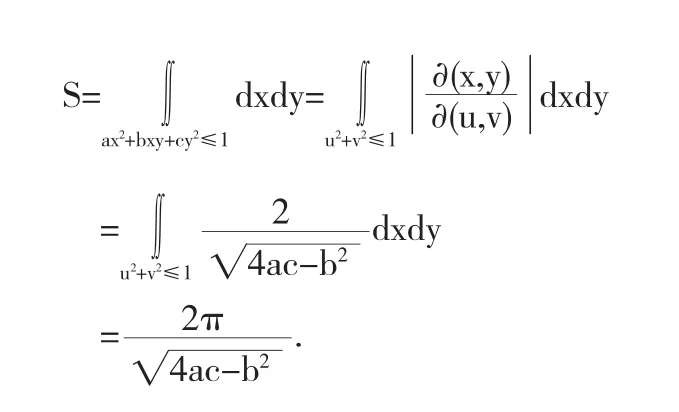
4 结束语
通过上述讨论,我们综合运用解析几何、微积分和线性代数的知识,给出计算一个中心在原点,但焦点不在坐标轴上的一般椭圆面积的六种方法.细心的读者不难发现,虽然六种方法考虑问题的角度与出发点各不相同,但是殊途同归,最终获得的结论是一致的,这正是数学问题一题多解的精髓所在.问题的思考与解决的过程,不仅可以让我们不断开拓思维,使思考问题的思路更加灵活,而且有助于我们进一步理清前后知识的脉络,达到融会贯通的效果.与此同时,文中所得到的椭圆 ax2+bxy+cy2=1(a>0,c>0 且 4ac-b2>0)面积之计算公式可以作为我们日常数学积累的一个结论,由此亦可帮助我们提升处理问题的效度和信度.
