前缘曲率对三维边界层内被激发出非定常横流模态的影响研究∗

陆昌根 沈露予

(南京信息工程大学海洋科学学院,南京 210044)(2018年7月11日收到;2018年7月29日收到修改稿)

三维边界层感受性问题是三维边界层层流向湍流转捩的初始阶段,是实现三维边界层转捩预测与控制的关键环节.在高湍流度的环境下,非定常横流模态的失稳是导致三维边界层流动转捩的主要原因;但是,前缘曲率对三维边界层感受性机制作用的研究也是十分重要的课题之一.因此,本文采用直接数值模拟方法研究在自由来流湍流作用下具有不同椭圆形前缘三维(后掠翼平板)边界层内被激发出非定常横流模态的感受性机制;揭示不同椭圆形前缘曲率对三维边界层内被激发出非定常横流模态的扰动波波包传播速度、传播方向、分布规律、感受性系数以及分别提取获得一组扰动波的幅值、色散关系和增长率等关键因素的影响;建立在不同椭圆形前缘曲率情况下,三维边界层内被激发出非定常横流模态的感受性问题与自由来流湍流的强度和运动方向变化之间的内在联系;详细分析了不同强度各向异性的自由来流湍流在激发三维边界层感受性机制的物理过程中起着何种作用等.通过上述研究将有益于拓展和完善流动稳定性理论,为三维边界层内层流向湍流转捩的预测与控制提供依据.

1 引 言

三维边界层内层流向湍流转捩的预测与控制一直是流体力学的前沿热点课题之一.边界层感受性问题是转捩过程的初始阶段,是实现边界层流动转捩预测与控制的关键过程.早期感受性问题的研究主要集中在二维边界层感受性问题,然而大多数工程实际问题都属于三维边界层流动,比如飞行器的后掠机翼表面、带攻角的圆锥以及流体叶片机械等.因此,三维边界层感受性问题的研究有着更加重要的理论意义[1].

通过风洞实验[2]发现,在低湍流度情况下,定常横流模态主导着三维边界层流动的转捩过程;在高湍流度情况下,非定常横流模态在三维边界层流动的转捩过程中占据绝对的主导作用.另外,风洞实验还发现,自由来流湍流是激发三维边界层内产生非定常横流模态的主要原因,而自由来流中的声波扰动在三维边界层内被激发出非定常横流模态的作用是十分微弱的,可以忽略不计.

早期的三维边界层感受性研究多数都集中在定常横流模态占主导的感受性过程,比如,Radeztsky等[3],Deyhle和Bippes[4],Reibert和Saric[5],Kurz和Kloker[6]分别研究了壁面局部粗糙的几何形状、大小和位置等因素对三维边界层感受性机制的影响;Betrolotti[7]以及Collis和Lele[8]研究了非平行性对三维边界层感受性机制的作用.直到最近,人们才开展涡扰动、自由来流湍流作用下三维边界层感受性问题的数值和实验研究.例如,Schrader等[9,10]采用直接数值模拟方法研究了自由来流涡扰动作用下三维边界层内被激发产生非定常横流模态的感受性过程.Tempelmann等[11,12]通过直接数值模拟方法和抛物化稳定方程法求解线性不可压Navier-Stokes方程,详细研究光滑后掠翼边界层内被激发产生非定常横流模态的感受性问题.Borodulin等[13]实验研究了自由来流涡扰动和壁面局部粗糙作用下三维边界层内被激发出非定常横流模态的感受性过程.本课题组近年来也开展了三维边界层内被激发出横流模态的感受性问题的相关研究[14,15],获得了一些有意义的结果.但是以上研究都忽略了平板前缘曲率变化对三维边界层感受性问题的作用.Lin和Malik[16]以及文献[17]的研究可知,前缘顶端曲率变化对二维边界层感受性过程有着显著的影响和作用.因此,开展不同前缘顶端曲率变化对三维边界层内被激发出非定常横流模态的感受性机制的作用研究具有重要的理论意义和实际应用价值.

2 控制方程和数值方法

2.1 控制方程

为便于研究,选取椭圆形前缘后掠翼平板为物理模型,并以椭圆形前缘的短轴长度b为特征长度、无穷远来流速度U∞为特征速度以及流体密度ρ为特征密度,可获得三维、无量纲不可压缩Navier-Stokes方程:

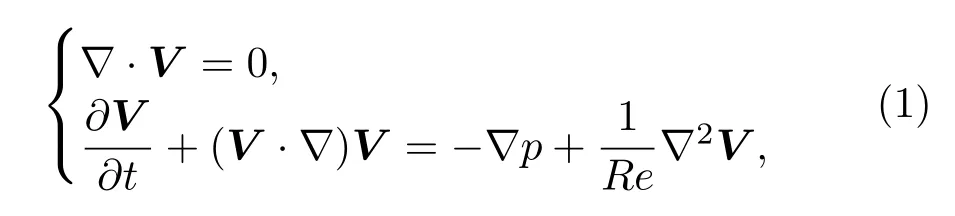
其中,速度为V=U+V′,V′={u,v,w}T为扰动速度,U={U,V,W}T为数值求解Navier-Stokes方程获得椭圆形前缘后掠翼平板边界层基本流;p为压力;雷诺数Re=(U∞b)/υ,且υ为流体的运动黏性系数.通过雅克比行列式变换将曲线坐标系(x,y,z) 化为直角坐标系(ξ,η,ζ)问题进行数值计算[18].控制方程的离散方法为:时间偏导数采用四阶修正后的Runge-Kutta格式;空间偏导数在x和y方向上采用紧致有限差分格式,即对流项为五阶精度迎风紧致有限差分格式,压力梯度项为六阶精度紧致有限差分,在z向采用傅里叶级数展开;黏性项为六阶精度紧致有限差分格式;压力方程利用四阶精度的有限差分格式迭代求解[19].

2.2 自由来流湍流模型

自由来流中的扰动主要有以下形式:声波扰动、涡波扰动以及自由来流湍流.声波扰动以压力脉动的形式来激发感受性机制,涡波扰动以单波扰动的形式来激发感受性过程以及自由来流湍流是以一群涡波扰动来激发感受性的物理现象.在自然界和工程技术实践中,自由来流湍流是普遍存在的;通过构造一组单波扰动组成的波群来模拟自由来流湍流模型,使研究课题更加接近于真实的物理问题.本文依据文献[20]的思想,构建各向异性的轴对称自由来流湍流模型,表达式为

其中,

且

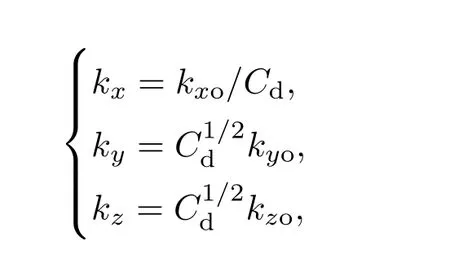
其中,Cd为轴对称的自由来流湍流的压缩系数;kxo,kyo和kzo是各向同性湍流的波数,ko=当压缩系数Cd=1时,自由来流湍流模型为各向同性湍流;而压缩系数Cd=1时,自由来流湍流模型为各向异性湍流.

2.3 计算区域和网格生成

图1为研究具有不同椭圆形前缘后掠翼平板边界层内被激发产生的非定常横流模态的感受性过程计算区域,其中,a为椭圆形前缘长轴,b为椭圆形前缘短轴;相对应的椭圆形前缘顶端曲率半径R∗=b2/a以及采用特征长度b无量纲化后的前缘顶端曲率半径R=b/a,则无量纲的前缘顶端曲率K=1/R;流向区域x∈[−50,600],且平板前缘的流向位置位于x=0;法向区域y∈[−11,11],展向区域z∈[−Z/2,Z/2],展向宽度Z=2π/κ3,后掠角ΦBS为无穷远来流U∞方向与x轴之间的夹角,本文选取后掠角ΦBS=45◦;雷诺数选为Re=2400;并采用泊松方程(3)[18]生成椭圆形前缘后掠翼平板在xoy平面上的贴体网格,z方向上则采用均匀网格.

图1 计算区域示意图Fig.1.Computational domain.

(3)式是通过源项函数P和Q控制网格在壁面处保持正交,并在平板前缘驻点以及壁面附近加密网格,以确保数值计算的准确性,计算网格数为800×200×16.

2.4 边界条件

壁面边界条件:壁面上采用无滑移条件,即扰动速度u=v=w=0,法向压力梯度∂p/∂n=0.

无穷远边界条件:扰动速度有自由来流湍流模型(2)式给出;压力p=0.

出流边界条件:压力梯度∂p/∂x=0;扰动速度采用无反射条件.

展向采用周期性边界条件.

3 数值结果与分析

本文研究在自由来流湍流作用下具有不同椭圆形前缘后掠翼平板边界层内被激发非定常横流模态的感受性过程,并通过流动稳定性理论证明在自由来流湍流作用下激发具有不同椭圆形前缘后掠翼平板边界层内被诱导非定常横流模态的感受性机制是真实存在的,具体过程与文献[15]相同,不再赘述.

本文重点关注的是不同椭圆形前缘顶端曲率变化对三维(后掠翼平板)边界层内被激发出非定常横流模态的感受性过程的作用;揭示具有不同椭圆形前缘顶端曲率情况下后掠翼平板(三维)边界层内被激发出非定常横流模态的感受性问题与自由来流湍流度、运动方向以及各向异性自由来流湍流等关键因素的影响.为方便比较,定义无量纲频率F=2πfυ/U2∞×106;数值计算发现,当y>6时边界层外缘的扰动速度均方根值,经长时间(t>500)计算趋于稳定值;定义边界层外缘的扰动速度均方根稳定值为自由来流湍流度AFST,其表达式为

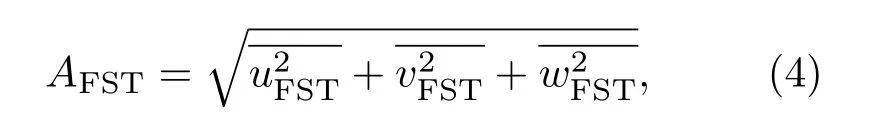
首先,研究各向同性自由来流湍流作用下具有不同椭圆形前缘三维(后掠翼平板)边界层感受性机制;选取压缩系数Cd=1,流向基本波数κ1=0.036,最大模数M=8,法向波数κy=0.01,展向波数κz=0.24.

图2给出了自由来流湍流作用下激发具有不同前缘顶点曲率情况的三维(后掠翼平板)边界层内产生非定常横流模态的流向扰动速度波包结构沿传播方向S的演化规律,波包传播方向与x轴之间的夹角为θg.由图2可知,当椭圆形前缘顶端曲率较小时,三维边界层内被激发出非定常横流模态的流向扰动速度波包的最大幅值沿传播方向S的演化趋势,要明显大于椭圆形前缘顶端曲率较大时三维边界层内被激发出非定常横流模态的流向扰动速度波包的最大幅值沿传播方向S的演化;但是,具有不同椭圆形前缘顶端曲率情况下,三维(后掠翼平板)边界层内被激发出非定常横流模态的流向扰动速度波包沿传播方向S的空间演化规律具有完全的相似性和对称性,且相位相同.

图2 在不同前缘曲率情况下三维(后掠翼平板)边界层内被激发出非定常横流模态的流向扰动速度波包沿传播方向S的演化 (a)K=4;(b)K=20;(c)K=40Fig.2.S-direction evolution of streamwise perturbation velocity wave packets of the excited unsteady cross- flow vortices in the three-dimensional(sweptplate)boundary layer with different leading-edge curvatures:(a)K=4;(b)K=20;(c)K=40.

跟踪记录不同时刻具有不同椭圆形前缘顶端曲率情况下三维边界层内被激发出非定常横流模态的流向扰动速度波包结构所有的最大值、最小值以及零点的位置,近似计算获得波包沿传播方向S的平均群速度以及波包传播方向S与流向x方向之间的夹角为θg,结果如表1所列.从表1可知,在不同椭圆形前缘顶端曲率情况下,三维边界层内被激发出非定常横流模态的扰动波波包传播方向以及传播的平均群速度几乎保持不变,它们之间的最大相对误差均小于1%.

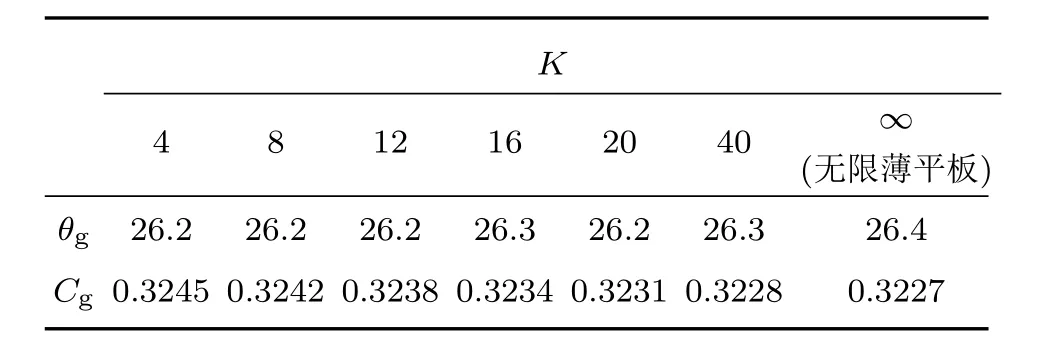
表1 三维边界层内被激发出的非定常横流扰动波波包传播方向和平均群速度Table 1.Propagation direction and average group speed of the excited unsteady cross- flow vortices in the threedimensional boundary layer.

数值计算了在不同前缘顶端曲率情况下三维边界层内被激发出非定常横流模态的感受性系数Λ.感受性系数Λ为三维边界层内被感受出非定常横流模态的扰动波波包的最大初始幅值ACF与自由来流湍流度AFST之比,数学表达式为

图3显示,当前缘顶端曲率K>2时,随着椭圆形前缘顶点曲率的不断增大,椭圆形前缘三维边界层内被激发出非定常横流模态的感受性系数Λ将快速衰减,直至衰减到某一阈值(K=25)后无论前缘顶端曲率如何增大,三维边界层内被激发出非定常横流模态的感受性系数Λ几乎趋于平缓状态.

其次,釆用时间傅里叶分析的方法,从图2中分别提取获得一组不同频率的非定常横流模态的扰动波.图4给出了在前缘顶端曲率K分别为4,20和40的情况下,三维边界层内被激发出的具有典型性两种频率的非定常横流模态的扰动波流向扰动速度沿传播方向S的演化过程.图4显示,无论椭圆形前缘顶端曲率如何变化,三维边界层内被激发出的具有典型性两种频率的非定常横流模态的扰动波流向扰动速度沿传播方向S的分布结构完全相似,且相位相同;惟一的区别是三维边界层内被激发出的非定常横流模态的扰动波流向扰动速度的幅值不同.即椭圆形前缘顶端曲率较小时三维边界层内被激发出的非定常横流模态的流向扰动速度的幅值要明显大于椭圆形前缘顶端曲率较大时三维边界层内被激发出的非定常横流模态的流向扰动速度的幅值.

依据图4具有不同椭圆形前缘三维(后掠翼平板)边界层内被激发出非定常横流模态的流向扰动速度沿传播方向S的演化规律,可以近似计算相邻波峰与波峰和波谷与波谷之间的幅值之比,并分别取对数后被波峰与波峰和波谷与波谷之间的距离相除后再取平均获得增长率,则近似求得具有不同椭圆形前缘三维边界层内被激发出非定常横流模态的扰动波的增长率沿传播方向S的演化,如图5所示.由图5可知,无论是椭圆形前缘顶端曲率如何变化,三维边界层内被激发出非定常横流模态的扰动波的增长率沿传播方向S的演化规律几乎保持不变,它们之间产生的最大相对误差约为1%.

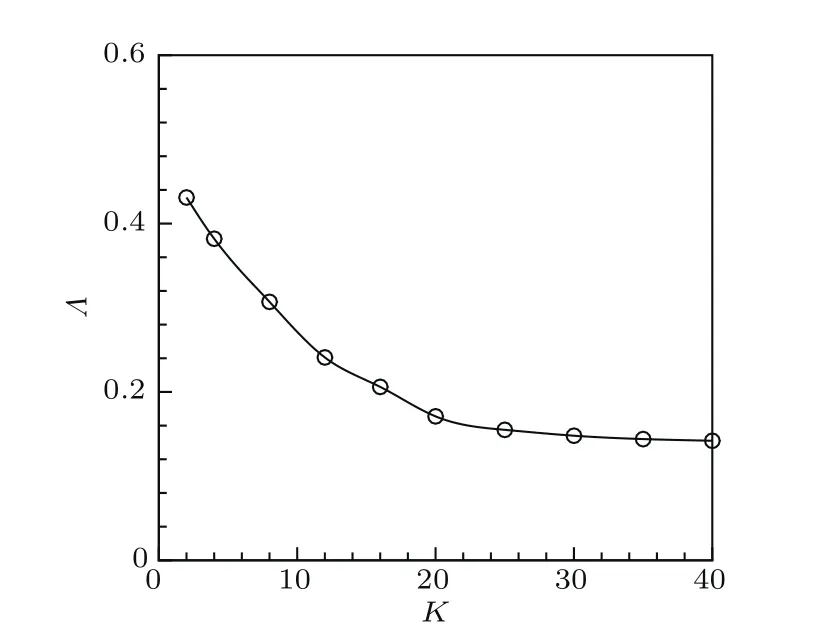
图3 三维边界层内被激发出非定常横流模态的感受性系数Λ与前缘顶端曲率K之间的关系Fig.3.Relation between leading-edge curvature K and receptivity coefficient Λ of the excited unsteady cross- flow vortices in the three-dimensional boundary layer.

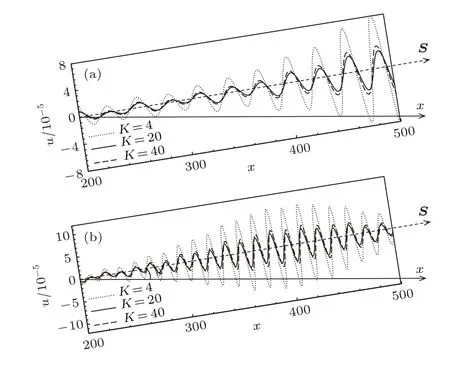
图4 三维边界层内被激发出的非定常横流模态的流向扰动速度沿传播方向S的演化 (a)F=30;(b)F=60Fig.4.S-direction evolutions of streamwise perturbation velocities of excited unsteady cross- flow vortices in the three-dimensional boundary layer:(a)F=30;(b)F=60.

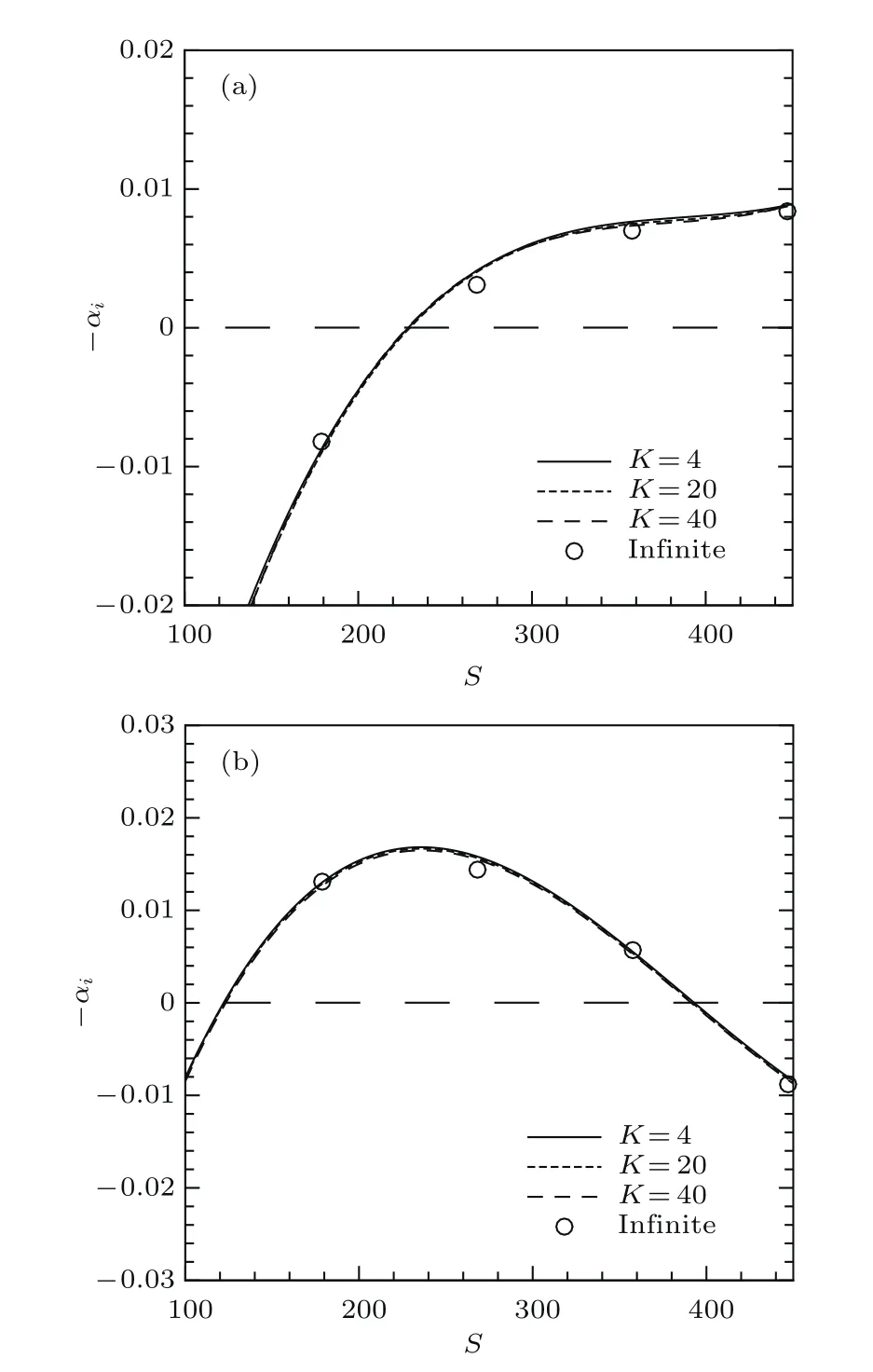
图5 三维边界层内被激发出的非定常横流扰动模态的增长率(−αi)在传播方向S 的演化 (a)F=30;(b)F=60Fig.5.S-direction evolutions of growth rates(−αi)of the excited unsteady cross- flow vortices in the threedimensional boundary layer:(a)F=30;(b)F=60.

再依据图4还可以求得三维边界层内被激发产生的非定常横流模态的扰动波的平均流向波数(或波长)以及沿流向传播的平均相速度,结果详见表2和表3.表2和表3分别列出了不同前缘顶端曲率情况下,三维边界层内被激发产生的不同频率非定常横流模态的扰动波的平均流向波数和平均相速度,结果发现无论是椭圆形前缘顶端曲率如何变化,三维边界层内被激发出非定常横流模态的所有扰动波的平均流向波数和平均相速度几乎保持不变,它们之间产生的最大相对误差为1%.

另外,同样在自由来流湍流作用下和在流向基本波数κ1=0.036以及最大模数M=8不变的基础上,数值研究除了法向波数κy=0.01和展向波数κz=0.24之外的其他不同的法向波数和展向波数情况下具有不同椭圆形前缘三维(后掠翼平板)边界层感受性机制,获得的结论与上述结论完全相同.

表2 具有不同椭圆形前缘顶端曲率情况下三维边界层内被激发出的非定常横流扰动波的平均流向波数Table 2.Average streamwise wave numbers of excited unsteady cross- flow vortices in the three-dimensional boundary layer with different leading-edge curvatures.

表3 具有不同椭圆形前缘顶端曲率情况下三维边界层内被激发出的非定常横流扰动波的平均相速度Table 3.Average phase speeds of excited unsteady cross flow vortices in the three-dimensional boundary layer with different leading-edge curvatures.

最后,研究自由来流湍流的强度和运动方向对三维边界层感受性问题的作用,并选取自由来流湍流基本波数κ1=0.036、法向波数κy=0.01、展向波数κz=0.24.

图6给出了在不同前缘顶端曲率情况下,三维边界层内被激发出的非定常横流模态的扰动波波包的最大初始幅值ACF与施加的自由来流湍流度AFST之间的关系(在图6中被感受出的非定常横流模态的扰动波波包的最大初始幅值ACF已被自由来流湍流度AFST=0.1%时被激发的非定常横流模态的扰动波波包的最大初始幅值A0归一化).从图6可知,无论是椭圆形前缘顶端曲率如何变化,当自由来流湍流度AFST61.0%时,三维边界层内被激发产生的非定常横流模态的扰动波波包的最大初始幅值与自由来流湍流度之间成线性增长规律.

图6 具有不同椭圆形前缘三维边界层内被激发出非定常横流模态的扰动波波包的最大初始幅值与自由来流湍流度AFST之间的关系Fig.6.Relation between free-stream turbulence intensity AFSTand initial amplitudes of excited unsteady cross- flow vortices in the three-dimensional boundary layer with different leading-edge curvatures.

由于真实的湍流运动一股都具有随机性和不确定性,因此,深入研究自由来流湍流运动方向对具有椭圆形前缘三维(后掠翼平板)边界层感受性问题的作用是很有意义的.在这里,仍选取自由来流湍流度AFST=0.1%保持不变,然后,通过分别改变自由来流湍流的流向波数、法向波数以及展向波数来改变自由来流湍流的运动方向,探讨自由来流湍流的运动方向对三维边界层感受性问题的作用和影响.为便于分析,自由来流湍流的运动方向采用图7所示的纬度角φ和经度角θ来表示.

在自由来流湍流的流向基本波数κ1=0.036和展向波数κz=0.24不变的情况下,通过改变法向波数κy来研究自由来流湍流的纬度角φ变化对三维边界层感受性问题的作用.图8给出了三维边界层内被激发出的非定常横流模态的感受性系数Λ与纬度角φ之间的关系.由图8可知,随着纬度角φ的不断增大,三维边界层内被激发出的非定常横流模态的感受性系数Λ将快速增长,直至纬度角φ约为−20◦时,感受性系数Λ达到最大值,随后当纬度角φ继续增大时感受性系数Λ将趋于较快的衰减过程.另外,从图8还发现无论纬度角φ如何变化,当椭圆形前缘顶端曲率越小时,三维边界层内被激发出的非定常横流模态的感受性能力就越强.

图7 三维角度示意图Fig.7.Three-dimensional angles.

图8 具有不同椭圆形前缘三维边界层内被激发出非定常横流模态的感受性系数Λ与纬度角φ之间的关系Fig.8.Relation between angle φ and receptivity coefficient Λ of excited unsteady cross- flow vortices in the three-dimensional boundary layer with different leading-edge curvatures.

在自由来流湍流流向基本波数κ1=0.025和法向波数κy=0.01不变的情况下,通过改变展向波数κz来研究自由来流湍流的经度角θ改变对三维边界层内被激发出非定常横流模态的感受性影响.由图9可知,当经度角θ630◦时,三维边界层内被激发出的非定常横流模态的感受性系数Λ增长十分缓慢;但是,当经度角θ>30◦后,三维边界层内被激发出的非定常横流模态的感受性系数Λ将快速增长.从图9还可获知,当椭圆形前缘顶端曲率越小时,三维边界层内被激发出非定常横流模态的感受性系数随经度角θ的增长将更加显著.

在工程实际中的自由来流湍流大多数都是各向异性的湍流,目前对各向异性湍流作用激发三维边界层内产生非定常横流模态的感受性机制研究的相关报道十分少见.因此,开拓各向异性的自由来流湍流作用激发三维边界层感受性机制方面的理论研究是十分有意义的.为便于研究,仅考虑各向异性的轴对称湍流.在这里通常改变轴对称自由来流湍流的压缩系数Cd来达到反映自由来流湍流的各向异性程度,当轴对称自由来流湍流的压缩系数Cd越大时,反映轴对称自由来流湍流的各向异性程度就越强;反之,当轴对称自由来流湍流的压缩系数Cd越小时,反映轴对称自由来流湍流的各向异性程度就越弱,也就越接近于压缩系数Cd=1情况下的各向同性自由来流湍流.

图9 具有不同椭圆形前缘三维平板边界层内被激发出非定常横流模态的感受性系数Λ与经度角θ之间的关系Fig.9.Relation between angle θ and receptivity coefficient Λ of excited unsteady cross- flow vortices in the three-dimensional boundary layer with different leading-edge curvatures.

本文选取自由来流湍流基本波数κ1o=0.036、法向波数κyo=0.01、展向波数κzo=0.24以及施加在外缘的自由来流湍流度AFST=0.1%.图10给出了在具有不同椭圆形前缘顶端曲率情况下,三维边界层内被激发出的非定常横流模态的感受性系数Λ与压缩系数Cd之间的联系.由图10可知,随着压缩系数Cd的不断增大,具有不同椭圆形前缘三维(后掠翼平板)边界层内被激发产生的非定常横流模态的感受性系数Λ也将快速增大,其原因可能是自由来流湍流的各向异性程度越剧烈,三维边界层内就越容易被激发出更强的感受性机制.另外,当椭圆形前缘顶端曲率越小时,三维边界层内被激发出非定常横流模态的感受性系数随压缩系数Cd的增长将更加显著.

图10 具有不同椭圆形前缘三维边界层内被激发出非定常横流模态的感受性系数Λ与压缩系数Cd之间的联系Fig.10.Relation between contraction ratio Cdand receptivity coefficient Λ of excited unsteady cross- flow vortices in the three-dimensional boundary layer with different leading-edge curvatures.

4 结 论

研究了前缘曲率对三维边界层内被激发出的非定常横流模态的作用,获得了如下结论.

1)在自由来流湍流作用下,无论是后掠翼平板前缘顶端曲率如何变化,三维边界层内都能被激发出非定常横流模态的感受性过程.当椭圆形前缘顶端曲率逐渐增大时,三维边界层内被激发出的非定常横流模态的感受性系数将快速衰减,直至前缘顶端曲率K约大于25后三维边界层内被激发出的非定常横流模态的感受性系数将趋于平稳状态;其次,无论后掠翼平板前缘顶端曲率大小是多少,三维边界层内被激发出的非定常横流模态的扰动波波包向下游传播群速度和传播方向完全相同以及波包沿传播方向上的空间演化结构具有完全的对称性和相似性,且相位相同;惟一区别是波包在空间分布的幅值大小不同而已.

2)通过时间傅里叶变换分析方法,从具有不同椭圆形前缘三维(后掠翼平板)边界层内被激发出非定常横流模态的扰动波波包中提取获得了一组不同频率扰动波.结果发现:无论是椭圆形前缘顶端曲率如何变化,三维(后掠翼平板)边界层内被激发出的一组不同频率扰动波的增长率、色散关系和相速度几乎保持不变;当椭圆形前缘顶端曲率越小时,三维边界层内被激发出的不同频率扰动波的幅值就越大;反之,当椭圆形前缘顶端曲率越大时,三维边界层内被激发出的不同频率扰动波的幅值就越小;也就是说椭圆形前缘非平行性影响越强,三维边界层内被激发出的非定常横流模态的感受性能力就越强;反之,椭圆形前缘非平行性影响越弱,三维边界层内被激发出的非定常横流模态的感受性能力就越弱.

3)自由来流湍流度与三维边界层内被激发产生的非定常横流模态的扰动波波包的最大初始幅值之间成线性增长关系.当自由来流湍流运动方向的纬度角不断增大时,三维边界层内被激发出的非定常横流模态的感受性系数将逐渐增长;直至当纬度角φ约为−20◦时,感受性系数达到最大值;当纬度角继续增大时,感受性系数开始趋于衰减状态.当自由来流湍流运动方向的经度角不断增大时,三维边界层内被激发出的非定常横流模态的感受性系数一开始增长得十分缓慢,直至经度角大于30◦后三维边界层内被激发出的非定常横流模态的感受性系数将快速增长.

4)不同自由来流湍流的各向异性程度对三维边界层感受性问题的作用研究发现:自由来流湍流的各向异性程度越剧烈,三维边界层内被激发产生的感受性能力就越强;反之,自由来流湍流的各向异性程度越弱,三维边界层内被激发产生的感受性能力就越弱.

5)数值计算结果还揭示出同一结论:在自由来流湍流作用下,当椭圆形前缘顶端曲率越小时,三维(后掠翼平板)边界层内就越容易被感受出非定常横流模态;反之,当椭圆形前缘顶端曲率越大时,三维(后掠翼平板)边界层内就越难以被感受出非定常横流模态.