基于PCA的遗传神经网络在套损预测中的应用

黄 军，孟凡顺,2，张 旭，杨冠雨

(1.中国海洋大学 海洋地球科学学院，山东 青岛 266100;2.海底科学与探测技术教育部重点实验室，山东 青岛 266100)

引 言

随着油田注水开采的发展，油田套管损伤明显增多，给我国油田造成了巨大的经济损失。套管损坏的原因非常复杂，很多时候石油生产专家都是通过个人经验来预测其破坏趋势[1-2]，但是经验的方法并不总能适用于一般情况。因此，套损预测研究具有重要的实际意义。目前有代表性的套损预测方法有：模糊数学法[3]、支持向量机法[4]、人工神经网络法等[5]，但支持向量机在应用时模型的参数选择困难，如惩罚参数、核函数的选取，而这些参数又在一定程度上影响着预测精度；模糊数学法模型的权重系数确定受到主观因素的影响；人工神经网络因具有自主学习能力强、记忆能力强、非线性并行处理能力强、容错能力强等特点，受到广泛的关注[6]，其中应用最多、最广泛的是BP(Back Propagation)神经网络。目前许多学者将BP神经网络用在地学问题的研究中[7-8]，但将其用于套损预测研究的并不多，且存在以下主要问题：一是当输入变量之间的相关性很强的时候，会增加不必要的输入维数，这不仅会导致神经网络的收敛时间迅速增长，也可能会出现由于某些变量对输出结果影响小而造成运算浪费[9]；二是BP算法在训练网络之前先要随机给定网络的初始权值和阈值，而不能给出一个最优值，而初始参数的选择会对网络的最终输出有很大的影响[10]。

1 基于主成分分析和遗传优化 BP 神经网络的套损预测模型

1.1 主成分分析的基本理论

主成分分析(Principal component analysis，PCA)可以将多个变量转化为少数几个能反映数据大致信息的综合指标，同时消除变量之间的相关性，其步骤为:

(1)对数据进行标准化。假设有n个样本，每个样本有p个指标，每个指标记为xij(i=1,2,…n;j=1,2,…p)。标准化后，

(2)建立变量的相关系数阵：

(1)

(3)计算R的特征值λi和特征向量：

αi=(αi1,αi2,…αip)T，i=1,2,…p。

(4)求取主成分Zi，

(2)

主成分分析的目的是为了提取到大部分的原始信息所携带的信息，而忽略那些携带信息较少的成分。在实际应用中，为了使原始信息得到充分利用，一般选取累计贡献率β(k)在85%之上的对应成分作为保留成分[11]。累计贡献率计算式为：

(3)

1.2 遗传算法优化BP神经网络

遗传算法(Genetic Algorithm，GA)是Holland于1962年提出的一种从生物世界进化演变而来的随机搜索方法，它具有良好的全局搜索能力。将遗传算法与BP神经网络相结合(以下简称GA-BP)，可以有效解决难以确定最佳网络初始参数的问题[12](图1)。

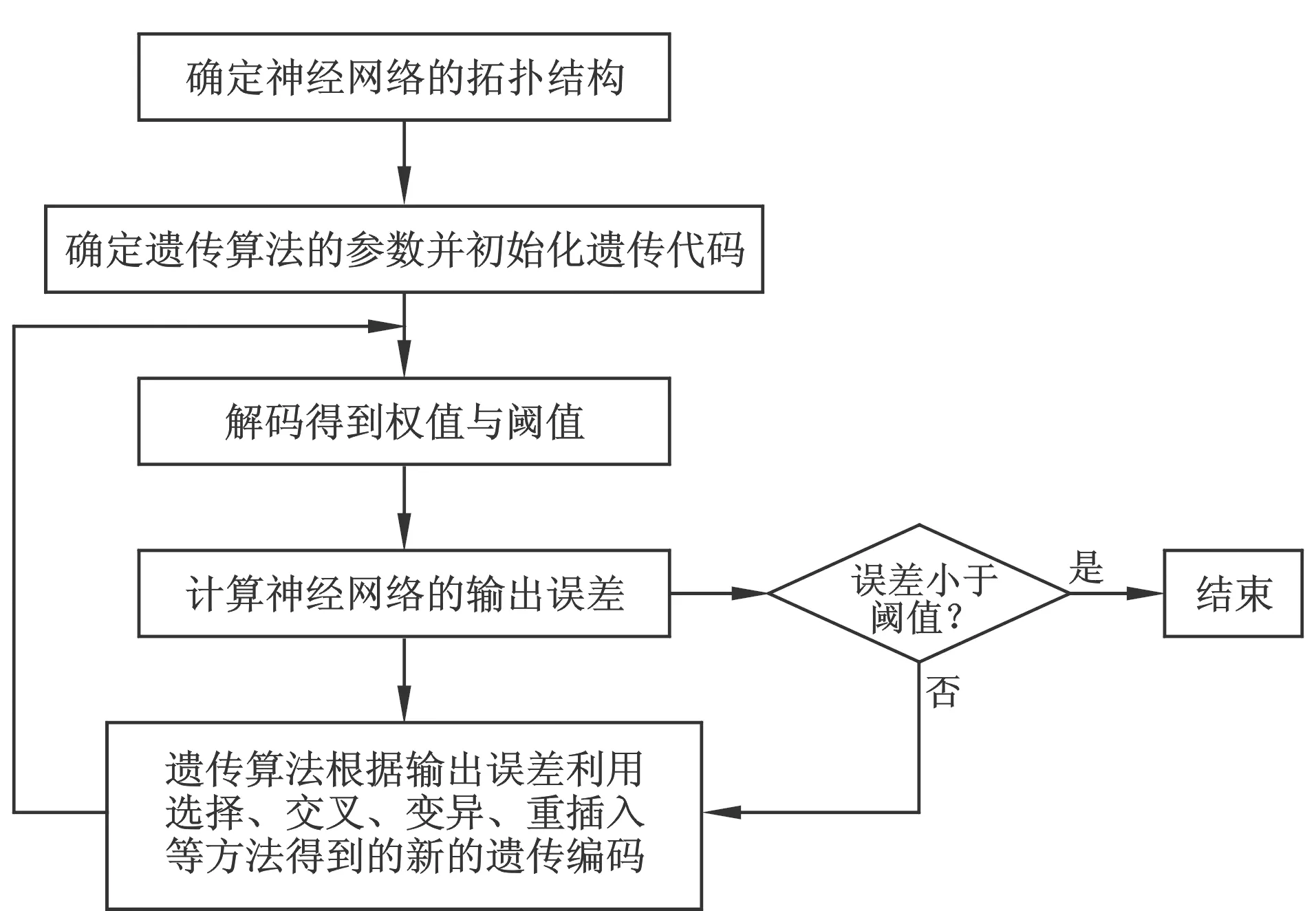
图1 遗传算法优化BP神经网络算法的流程图Fig.1 Flow chart for optimizing BP neural network using genetic algorithm

1.3 套损预测模型的建立

首先对原始数据进行主成分分析，将主成分提取出来并将其作为神经网络的输入，在训练神经网络之前，先用遗传算法进行迭代，确定最佳的网络权值和阈值，最后再利用BP神经网络进行套损预测(以下简称PCA-GA-BP)，模型结构如图2所示。

图2 PCA-GA-BP套损预测模型结构Fig.2 PCA-GA-BP model for forecasting of casing damage

2 南一区套损预测数据选取

引起套损的因素是多种多样的，从大类可以分为地质因素、工程因素以及腐蚀因素。其中地质因素包括油层出砂、泥岩蠕变、断层影响等[13-15]；工程因素包括固井质量、射孔、注水情况等[16-18]等。本文研究区域为大庆油田南一区西西区块，该区位于萨尔图背斜构造中部及西翼，构造轴向北北西向，构造东高西低，东翼倾角3°～7°，西翼倾角为5°～10°，区域内断层比较发育，倾向为南西和北东向，图3展示了研究区域的具体位置。该区于1960年投入开发，先后部署5套开发井网，目前井网密度为93.1口/km。基础井网分2套层系开采：第一套是开采葡一组层系，第二套是开采萨+葡二组油层中、高渗透油层的层系，采用不规则四点法面积注水[19]。综合考虑南一区的实际情况以及套损影响因素，将表1所列作为研究内容。从南一区西西区块选取该区域油井116口，水井216口，其中油井部分选取96口井作为训练集，20口井作为预测集，水井部分随机选取176口井作为训练集，40口井作为预测集。

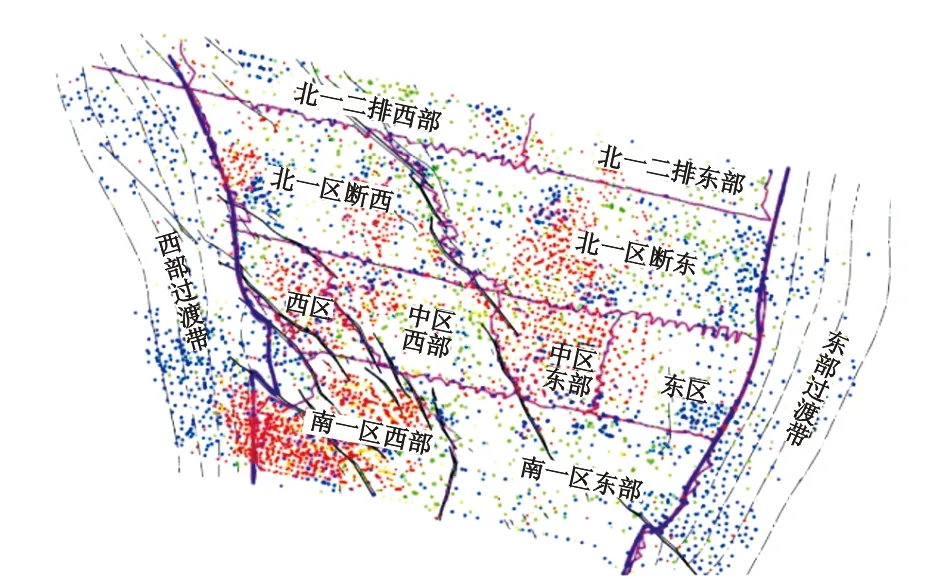
图3 研究区域位置Fig.3 Regional location of the study area

编号代号详细描述1t生产时间2cx层系,依据实际生产划分的层系分类3s射孔层厚度4dc1距离井最近的断层5dc2是否钻遇断层6bh套管壁厚度7gj套管钢级8yy1统计时间内最大油压9yy2截止时间前1a内的平均油压10ty1统计时间内最大套压11ty2截止时间前1a内的平均套压12rz1统计时间内最大日注水量(限水井)13rz2截止时间前1a内的平均日注水量(限水井)14lz截止时间前1a内的累计注水量(限水井)

3 模型的处理结果及其分析

3.1 BP神经网络训练结果分析

3.1.1 网络结构及参数选择

首先对输入输出数据进行归一化，建立BP网络，采用LM(Levenberg-Marquart)方法优化网络[20]，激活函数选择tansig函数。动量因子取0.95，训练目标0.000 01。神经网络均为3层结构，即1个输入层，1个隐含层以及1个输出层，具体结构为油井11×7×1,水井14×12×1。

3.1.2 结果分析

BP神经网络预测套损结果如图4所示。从图4可以看出，BP神经网络在预测套损情况时，准确率非常低，油井预测准确率为60%(用时0.7 s)，而水井只有55%(用时1.3 s)。

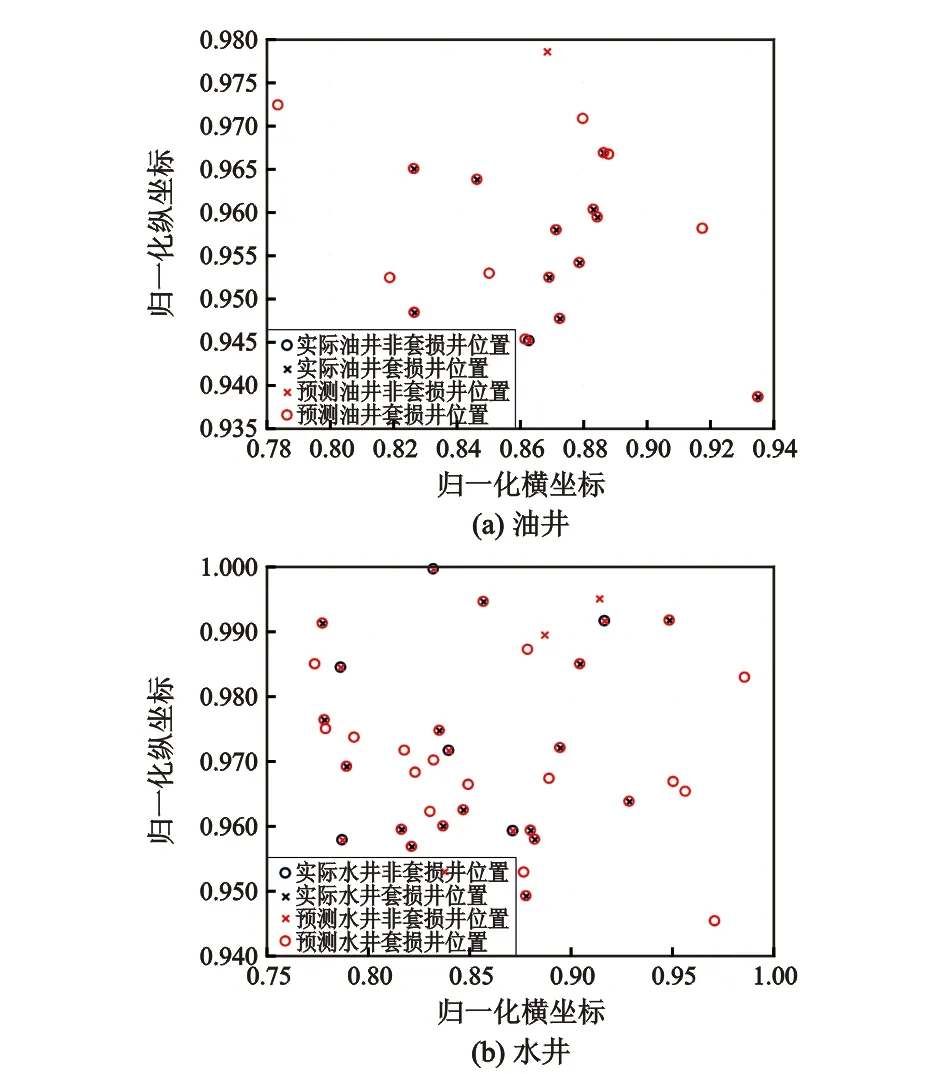
图4 BP神经网络模型预测结果Fig.4 Forecast results of casing damage by BP neural network

3.2 PCA优化的BP神经网络训练结果分析

首先将采集到的数据进行主成分分析，然后将满足要求的主成分作为神经网络的输入进行训练。表2和表3分别列举了油水井累计贡献率β(k)大于85%的各个主成分。

表2 累计贡献率大于85%的主成分统计(油井)Tab.2 Statistics of the principal components whose cumulative contribution is higher than 85%(oil well)

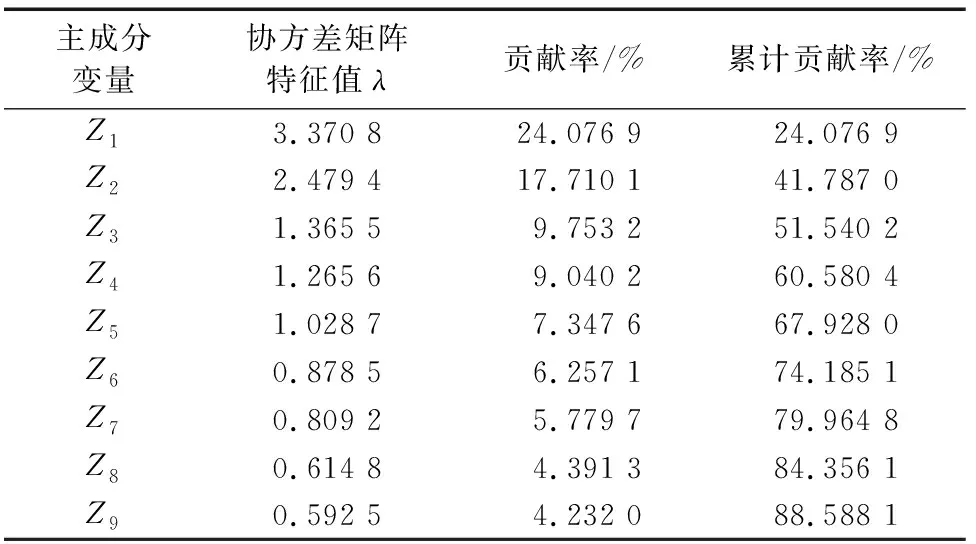
表3 累计贡献率大于85%的主成分统计(水井)Tab.3 Statistics of the principal components whose cumulative contribution is higher than 85%(water well)

由于主成分分析后的数据维度降低，将新的数据带入之后，油井预测准确率60%，运算时间0.6 s；水井预测准确率60%，运行时间0.9 s，可以看出PCA降维处理后的数据在提高BP神经网络的性能方面并没有起多大作用，经PCA优化的BP神经网络(简称PCA-BP)运算结果如图5所示。

图5 PCA优化的BP神经网络预测结果Fig.5 Forecast results of casing damage by PCA-BP neural network

3.3 GA算法优化的BP神经网络训练结果分析

3.3.1 遗传算法的参数选择

遗传算法是用适应度函数来判断个体优劣的，本文用网络输出与实际结果的误差绝对值之和作为适应度函数。油井的权重个体的基因位数为92，初始种群数目为50，交叉概率0.8，变异概率0.001，选择基于轮盘赌的选择操作，最大迭代次数为50；水井权重个体的基因位数为193，初始种群数目为100，交叉概率0.9，变异概率0.01，选择基于轮盘赌的选择操作，最大迭代次数为50。

3.3.2 运算结果对比分析

对油井数据进行分析，可以看出经过遗传算法优化的神经网络的输出准确率为75%，水井部分的预测准确率为72.5%。如图6示，油井部分出现5口井预测错误，水井11口井预测错误。说明经过遗传算法优化后神经网络的预测能力显著提高。

3.4 基于PCA的遗传神经网络(PCA-GA-BP)训练结果分析

如上所述，主成分分析可以降低输入项的维度，简化神经网络的结构。经过PCA处理后的油井数据有6个主成分，水井则有9个。因此在这里油井的神经网络结构为油井6×7×1,水井9×12×1。其他参数与3.3节对应参数相同。图7分别是油井未经PCA降维处理的适应度曲线与经过PCA处理的适应度曲线，从图7可以看出，未经PCA处理的油井数据直接运用遗传神经网络进行训练，其适应度曲线虽然在经过10次迭代以后适应度变换缓慢，但始终没有趋于平稳，而经过PCA处理的遗传神经网络的误差则在20代之后就几乎不变，且最大适应度与平均适应度也慢慢重合，这说明最佳种群长时间不进化，也就意味着找到了最优目标值。

图8为经过PCA处理后的预测结果，从图可以看出，油井有3口井预测错误， 准确率为85%；水井部分的准确率为82.5%。说明PCA-GA-BP模型的预测准确率较为理想。

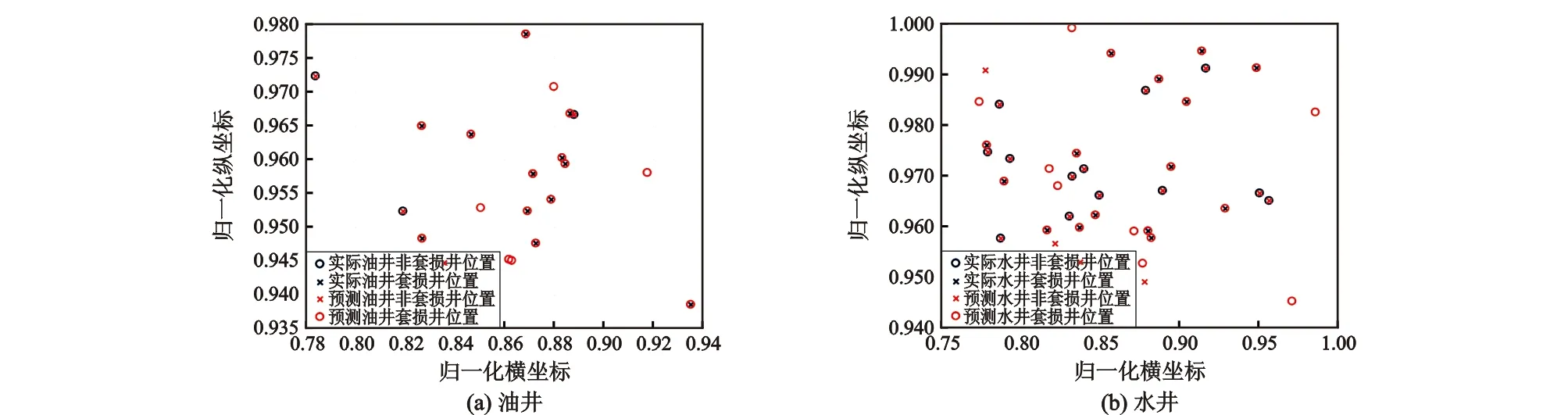
图6 GA优化的BP神经网络预测结果Fig.6 Forecast results of casing damage by GA-BP neural network

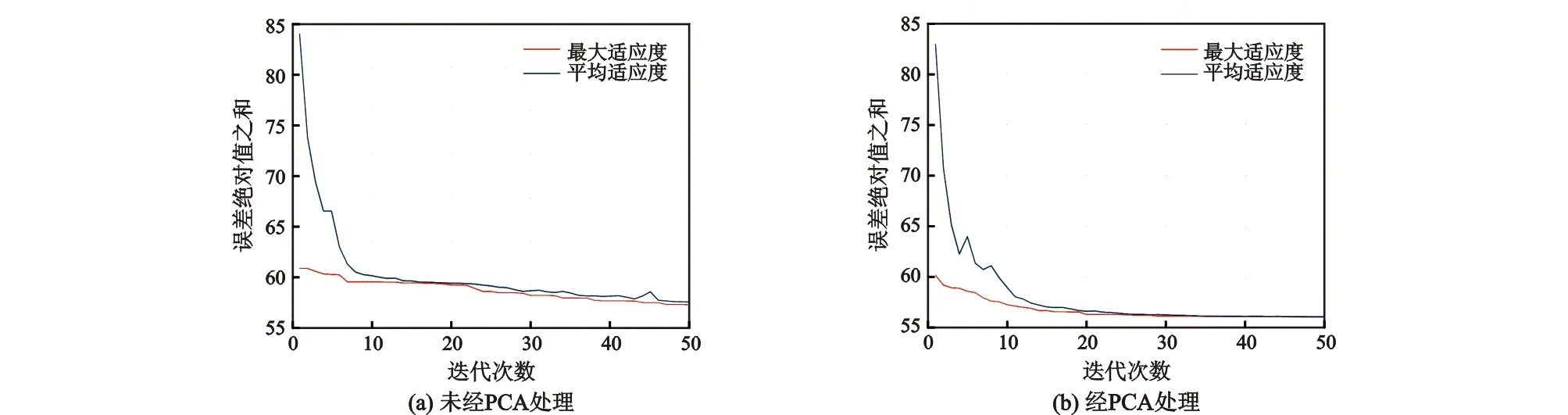
图7 油井数据的遗传神经网络误差对比Fig.7 Comparison of oil well fitness curves of BP neural network and PCA-BP neural network

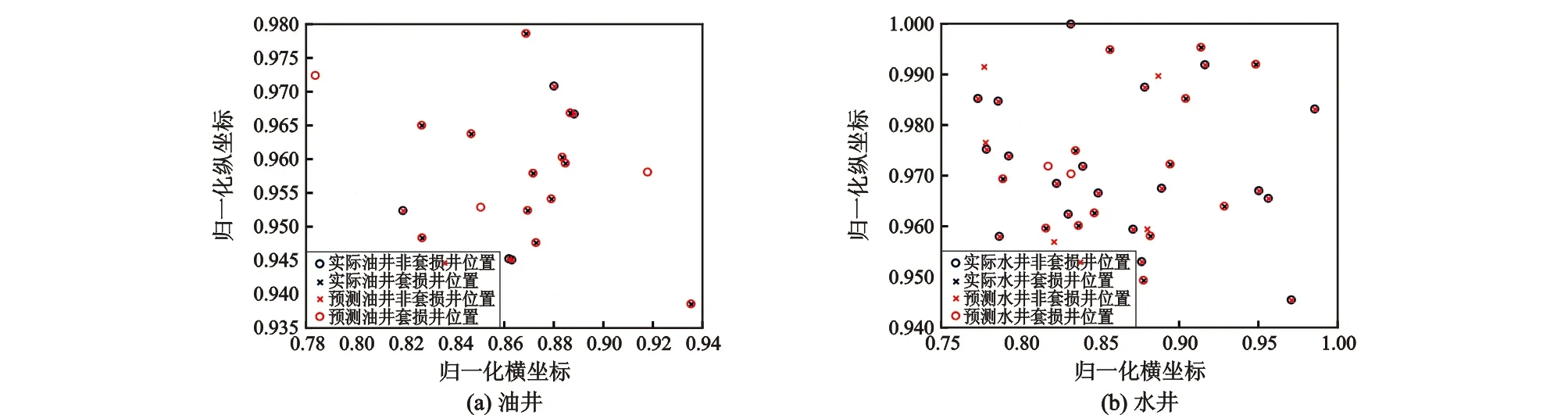
图8 PCA处理的GA-BP神经网络预测结果Fig.8 Forecast results of casing damage by PCA-BP neural network

3.5 总结及分析

综上分析，可以看出PCA-GA-BP神经网络结构对套损问题有一定的预测能力。相比于单纯地使用神经网络，PCA通过减小输入数据的维度，简化神经网络的复杂度，可以减小网络的运行时间。但是PCA并不能解决神经随机初始参数的问题。而遗传算法GA则可以很好地优化网络初始值，进而使整个神经网络的预测能力得到大幅度提高，经过PCA优化的遗传神经网络比未经PCA处理的神经网络更加精确。为了便于对各方法有一个全面的了解，表4列举各种方法的预测准确率以及运行时间。

表4 各种方法计算结果统计Tab.4 Calculation effects of different BP neural networks

从表4可以看出，PCA-GA-BP神经网络相比于其他模型准确率最高。

4 结 论

本文建立了基于主成分分析的遗传神经网络模型，并采用该模型对大庆油田南一区套损情况进行预测，数据结果显示此模型在准确率上有很大的提高。从中可以得出以下结论:

(1)BP神经网络模型准确率易受到输入项的数据本身及初始参数选取的制约。

(2)PCA在降低数据相关性、减小神经网络的输入维数、优化网络结构方面有很好的效果，但需要避免随机给定网络初始参数的问题。如果不对初始参数进行优化，尽管模型的运行时间因为输入数据的维度变小而变少，但准确率并没有得到明显提高。

(3)利用遗传算法可以很好地处理神经网络初始参数无法确定的问题，经过GA算法处理的神经网络的预测能力比BP神经网络有很大的提高。将PCA方法应用于GA-BP神经网络，使得网络经较少次数迭代即可趋于稳定，求得最优初始参数，进而得到最高的准确率。