基于双高斯函数的一种高效鸟群优化算法
2018-11-30彭君君刘勇进
彭君君,刘勇进
(1.沈阳航空航天大学 计算机学院,辽宁 沈阳 110136;2.沈阳航空航天大学 理学院,辽宁 沈阳 110136)
0 引 言
最优化问题是一类重要的数学问题,普遍存在于工程实际和应用中,其中包括连续、离散、光滑、非光滑、凸和非凸等类型。对于具有良好数学特性的问题,如凸规划,已经有很多成熟的数值方法求解,如内点法[1-2],但是工程实际和应用中的优化问题往往是复杂的,具有非凸和高度非线性等特性。因而,传统的优化方法并不能有效求解,于是一种模拟生物进化和仿生自然界动物觅食筑巢行为的启发式智能优化仿生算法应运而生。仿生优化算法一般建立在生物智能或物理现象基础之上,通过模拟某些自然现象或过程求解复杂优化问题。目前常见的智能优化算法有:粒子群算法(PSO)[3-4]、人工鱼群算法(AFSA)[5]、人 工蜂群算法(ABC)[6]、布谷鸟搜索算法(CS)[7]、蝙蝠算法(BA)[8]等,各种群体智能算法在求解最优化问题中侧重点不同,因此各有优缺点。
为了使其获得更好的寻优特性,文献[9]根据自然界鸟群觅食、警觉和迁移等生物行为提出一种新型生物启发式算法——鸟群算法。鸟群算法根据鸟群生存特性,通过构建觅食行为、警觉行为、迁徙行为的机制完成整个鸟群的繁殖生存(迭代寻优),相比传统群体智能算法拥有更良好的寻优特性。但是鸟群算法也存在许多局限性,例如:在进行觅食行为和警觉行为过程中,基本鸟群算法在每一次迭代时都依赖于之前迭代求得的个体最优值和群体最优值,若上一次的个体最优或群体最优值陷入局部极值点时或者陷入别的极坏情况(如鞍点[10]),则种群易陷入局部最优或者徘徊于当前迭代值并导致收敛极慢。在基本鸟群算法的迁徙行为中,其只依赖于简单的随机函数,忽略了算法已产生的寻优信息,不能根据当前寻优空间的变化而变化,浪费了寻优资源。在整个基本鸟群算法中,鸟群个体的寻优方向都趋向于当前生产者的寻优方向,这可能导致算法处于固化状态,即下一次迭代的寻优方向很难摆脱上一次生产者的寻优方向,致使种群缺乏多样性,进而导致算法寻优速度缓慢。
针对基本鸟群算法存在的局限性,人们充分重视鸟群寻优过程产生的寻优信息,研究种群寻优时表现出的种群特性,并添加人为影响寻优空间多样性的更新机制,构建改进的高效鸟群优化算法。新算法在原算法的基础上添加挑食行为,即在鸟群开启群体行为之前,通过挑食行为选择鸟群中的个体最优值与群体最优值,避免算法一开始就陷入比较坏的情况;在鸟群的迁徙行为中,加入智能学习寻优行为,有效地避免鸟群寻优过程中的盲目性;同时构建能够更好地避免群体智能算法早熟的双高斯函数更新法[11-13],对于鸟群每次迭代之后,在保留群体最优个体的基础上,将会淘汰一部分不具有优势的弱势个体,然后通过双高斯函数生成新一代鸟群个体,拓展种群多样性,提高算法的全局搜索能力。
本文构建基于双高斯函数的高效鸟群优化算法,并通过对具备不同测试特性(单峰/多峰、低维/高维、可分/不可分)的多种典型标准测试函数(Benchmark)进行最优化寻优仿真。仿真结果表明,改进的智能鸟群算法在对各种类型标准函数寻优时均具备稳定性,同时可以较好地避免算法早熟。
1 基本鸟群算法
鸟群算法(BSA)[9]是通过模仿鸟群的觅食行为、警觉行为和迁徙行为的一种新型生物启发式算法。鸟群算法模仿的生物行为可简化为如下规则:
1)鸟群中的每一只鸟可自由选择觅食行为或警觉行为。
2)鸟群处于觅食状态时,每只鸟即时记录并更新其所经过的最佳觅食位置,并记录种群最佳觅食位置,同时将此信息分享至整个鸟群。
3)鸟群处于警觉状态时,每只鸟试图飞往种群的中心,这种行为会因种群间的竞争而受到影响,食物储存多的鸟比储存少的有更大的几率飞往鸟群中心。
4)鸟群会按周期性地飞往另外一区域。种群中食物储存最多的称为生产者,储存最少的称为乞食者,其他的鸟随机选择作为生产者或乞食者。当鸟群从一个区域飞往另一个区域,各只鸟的角色都将发生改变。鸟群之间会分享所寻觅的食物信息,这一习性使得种群更有利地生存下去。
5)生产者积极寻找食物,乞食者随机跟随一位生产者寻找食物。
假设有N只鸟在D维空间中飞行觅食,第i只鸟Xi在j维空间t时刻的位置为xti,j,i=1,2,…,N;j=1,2,…,D,规则1)可被表述为一个随机决策过程。以均匀概率在(0,1)之间产生的一个随机数,同时设定一个常数P∈[0,1],若随机数大于常数P,鸟觅食,否则保持警觉。
1.1 觅食行为
基于规则2),鸟群的觅食行为服从每只鸟自身积累的经验以及群体经验,觅食行为的位置更新公式为:
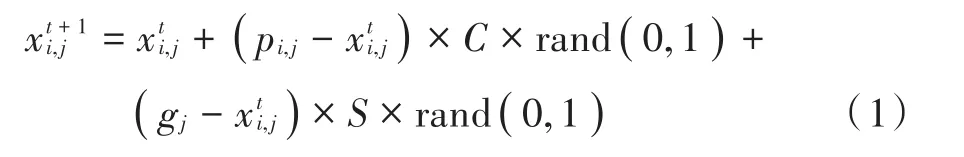
式中:rand(0,1)表示[0,1]范围内独立均匀分布的随机数;为鸟更新的位置;为鸟当前所在位置;pi,j为第i只鸟经过的最佳位置;gj为种群最佳位置;C,S为两个正的常数,分别称为认知系数及社会进化系数。觅食行为在每一次更新时都依赖于已求得的个体最佳位置和种群最佳位置,当已知的个体最优或种群最优值陷入局部极值点或者鞍点[10]时,算法易陷入局部最优或者徘徊于当前迭代值。
1.2 警觉行为
对于规则3),鸟群在保持警戒状态下竞争地尝试飞往种群中心,这种行为的数学表达式如下:

式中:meanj为整个种群平均位置的第j个元素;a1,a2是[0,2]之间的常数;k(k≠i)是[1,N]之间的随机整数;pk,j为第k只鸟所经过的最佳位置;pFiti为第i只鸟的适应度值;sumpFit为整个种群的适应度之和;N为种群的规模;ε用来避免零分割,是计算机里最小的常数。A1的含义是其中一只鸟向种群中心移动过程中由环境引发的间接作用,而A2阐述的则是由某个具体竞争冲突而引发的直接作用。由上述可知,警觉行为也严重依赖于之前迭代求得的个体最佳位置。
1.3 迁徙行为
针对规则4)和规则5),鸟群因为逃避追捕或寻找食物等原因,会定期飞往其他区域。当到达另一区域后,它们会重新觅食,一些作为生产者的鸟开始寻找食物,其他鸟跟随生产者寻觅食物。生产者和乞食者可由规则4)从种群中筛选,生产者和乞食者的行为可描述为:
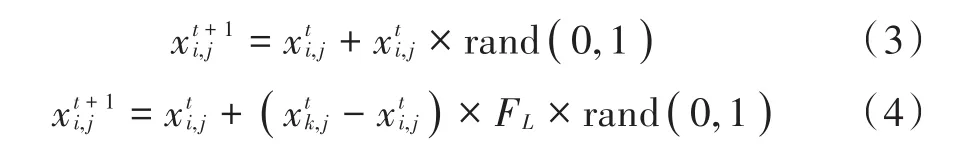
式中:rand(0,1)代表服从期望值为0,标准差为 1的高斯分布的一个随机数;k∈[1,N],且k≠i;FL(FL∈[0,1])为乞食者随同生产者觅食的概率。鸟群的迁移有一个固定的周期,设为FQ,FQ为正整数。迁徙行为仅依据简单的随机函数,不能依据当前寻优空间的变化而变化,浪费了寻优资源。
分析整个基本鸟群算法可知,鸟群个体的寻优趋势为向当前生产者的寻优方向靠近,这可能导致算法下一次迭代的寻优方向很难摆脱上一次生产者的寻优方向,致使种群缺乏多样性,进而导致算法寻优速度缓慢。
2 高效鸟群优化算法
高效鸟群优化算法(EBSA)在原算法的基础上添加挑食行为、智能学习行为和双高斯函数更新法则,保障鸟群优化算法拥有更佳的寻优能力和收敛性质。
2.1 挑食行为
在鸟群处于觅食行为与警觉行为时,鸟群算法依赖于当前的个体最优位置pi,j与种群最优位置gj,原始的鸟群算法只简单选取了当前最优值,若其处于比较坏的情况时(局部极值点、鞍点),则严重影响算法的寻优方向。在本文中添加一个挑食行为,即令鸟群在每一次迭代过程中对当前最优值再进行一次小范围的寻优,避免上述情况的发生。当前鸟群最优个体i在第j维空间时第m个挑食位置的计算公式为:
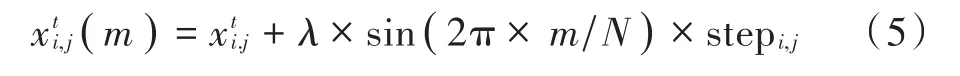
式中:m∈{1,2,…,N}为挑食次数;随机因子λ为[-1,1]均匀分布的随机数;stepi,j为第j维的挑食步长,一般取0.1。
根据当前最优值的小范围扩散准则,当前最优鸟群个体Xi在t时刻第j维上生成的m个挑食点位置可用集合表示为选择适应度最大值,设为并与当前最优鸟群个体的适应度值fpi,j和当前最优种群适应度值fgj相比较,若挑食最大适应度值pFitmaxi大于fpi,j,则个体最优位置pi,j更新为pFitmaxi对应位置,个体最优适应度值fpi,j=pFitmaxi。若鸟群个体的最优适应度值大于种群最优个体所对应的适应度值,则该个体将代替种群最优个体,即gj=pi,j,fgj=fpi,j。若pFitmaxi<fgj,则保持原种群最优个体不变。挑食行为可重复进行,最多不超过Tmax。挑食行为结束时,确定种群最优个体位置及其适应度值,进入下一步。
2.2 智能学习行为
为了更好地利用优化算法当前已产生的寻优信息结构,在鸟群的迁徙行为中加入智能学习行为,即当生产者确定后,生产者通过信息告诉乞食者自己的位置及适应度值,乞食者Xi通过判别自身位置的适应度值与生产者Xk的位置及其适应度值的差距,以智能学习步长逼近生产者所在的位置。乞食者第j维空间位置由智能学习前位置、智能学习步长和学习方向决定,即:
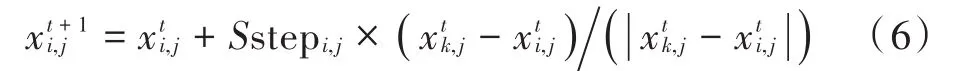
式中:Sstepi,j为乞食者Xi进行智能学习时第j维的智能步长;k表示生产者中随机选择的一个个体。智能学习步长表示乞食者Xi在学习空间中向具有最优适应度值的生产者趋近的移动幅度。为了获得更好的寻优效率,乞食者自身适应度值与生产者适应度值之间的差距越大,则学习步长越大;反之,当乞食者自身适应度值与生产者适应度值之间的差距越小时,学习步长越小;当乞食者自身适应度值与生产者适应度值之间无差距时,乞食者根据适应度值环境限制以最小步长进行寻优。以寻优空间和寻优空间中最优适应度值与最劣适应度值之差为基准,取乞食者智能学习步长与乞食者适应度值和生产者适应度值差形成正相关关系来构建智能学习步长,即:
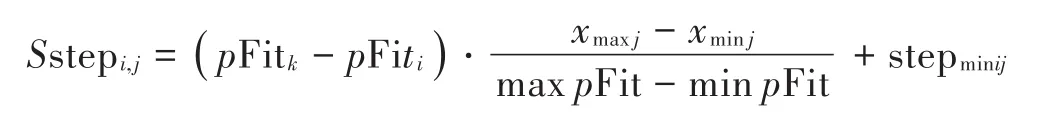
式中:xmaxj,xminj分别为鸟群在当前第j维寻优空间最大、最小边界值;maxpFit,minpFit分别为xmaxj,xminj对应的鸟群最优食物资源和最差食物资源;stepminij为乞食者寻优过程中受环境等原因限制时的最小步长,为非负数。
2.3 基于双高斯函数的鸟群更新规则
为了更好地保持鸟群多样性,避免陷入局部最优,在进行智能学习行为后,根据寻优空间的状态平衡,以“优胜劣汰”自然法则淘汰其中最差的Q只鸟,并重新生成与淘汰个体同等数量的鸟群个体数,这里Q取[N(2β),N β]之间的随机整数,β为群体更新比例因子。为了更好地提高鸟群的种群多样性,设计一种双高斯函数更新法,通过构建双高斯函数,使得新生个体的位置远离原淘汰个体所处的不具备良好种群多样性的位置。定义新生个体第j维的位置为:
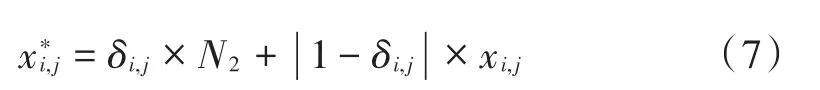
式中:δi,j为新生个体第j维更新系数,该系数为随机生成的0或1,用以确定该维位置是否更新;N2为基于双高斯函数的新生个体位置更新系数。从概率统计的角度来看,鸟群新生成个体之间的差别是许多微小的独立随机因素影响的结果。根据中心极限定理可以认为,新生成鸟群位置差别具有正态分布特性。同时,为了促使新生成个体更好地逃离原淘汰个体所处的位置,本文通过双高斯函数生成新鸟群个体,越是远离原个体位置的点,成为新生个体的概率越高,即:

式中:σ1和σ2为双高斯函数的均方差;e为符合标准正态分布的随机数;r1为隶属于[0,1]间的随机数,用以促使新生成个体倾向于向更加远离原区域的位置逃离;θ(x)为阶跃函数,具体定义如下:
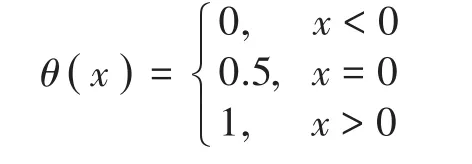
一旦新生成个体的第j维位置超出寻优空间的范畴,则重新进行双高斯位置更新,直至新生个体第j维新生位置处于寻优空间内。
2.4 高效鸟群优化算法步骤及时间复杂度分析
2.4.1 高效鸟群优化算法的步骤
高效鸟群优化算法的步骤如下:
Step1:初始化鸟群X和相关参数。
N:鸟群个体的数目;M:最大迭代次数;Tmax:最大挑食次数;FQ:鸟群迁徙周期;P:觅食的可能性;C,S,a1,a2,FL,step,β七个常数。
Step2:评估N个个体的适应度值和最优解,而且令t=1。
Step3:鸟群最优个体以式(5)进行挑食行为。
Step4:判断t%FQ≠0,若成立,则对鸟群的N个个体分别在rand(0,1)里取随机数,若随机数小于P,则该个体以式(1)形式进行觅食;若随机数大于P,则该个体以式(2)形式进入警觉行为;否则,进入下一步。
Step5:求出鸟群N个个体中的生产者和乞食者,并且乞食者以式(6)形式向生产者进行智能学习。然后,生产者以式(3)形式进行迭代;乞食者以式(4)形式进行迭代。
Step6:针对上述更新得到的N个鸟群个体,挑出最差的Q个个体(Q≪N),按式(7)的双高斯函数形式进行迭代更新。
Step7:判断得到的最优解是否优于已有最优解,若满足,则更新鸟群最优值;否则,进入下一步。
Step8:令t=t+1,判断t≤M是否成立,若成立,转Step2;否则,算法终止。
2.4.2 高效鸟群优化算法的时间复杂度
基于双高斯函数的高效鸟群优化算法时间复杂度可以根据2.4.1节的算法详细步骤求得。高效鸟群优化算法的时间复杂度[14-15]主要花费于解在寻优空间里的产生、评估和更新,其所需要的最大计算量可称为时间复杂度,而其他简单计算可忽略。基本鸟群算法[9]的时间复杂度为O(MN)(详见参考文献[9]),影响其主要复杂度的因素为最大迭代次数和鸟群个体数目。为了提高高效鸟群优化算法的收敛性能和处理复杂函数的寻优能力,引入挑食行为、智能学习行为和双高斯函数更新法则,致使算法在时间复杂度上有一定的提高。挑食行为由于在算法的每次迭代中增加了最多Tmax次运算,其时间复杂度为O(Tmax),且Tmax一般取N的20%左右,增加幅度并不大。由于智能寻优行为只针对每一次迭代的生产者和乞讨者,其增加的复杂度可忽略不计。对于双高斯函数更新法则,其在算法的每一次迭代时选择Q个劣等个体进行更新,Q一般取N的25%左右。综合上述行为,由增加的时间复杂度可得高效鸟群优化算法的时间复杂度为O(MN2),由于N≪M,因而这种程度的计算开销增加是完全可以接受的。
3 仿真实验及算法测试
为了验证本文提出的EBSA的有效性和实用性,选用具有不同特性的9个标准测试函数进行算法有效性测试。
3.1 标准测试函数
标准测试函数包括单峰函数与多峰函数、可分函数与不可分函数、低维函数与高维函数。单峰函数仅有一个极值,即局部极值就是全局最优值[16],可以很好地验证算法寻优的快速性;多峰函数一般有多个局部极值,在验证算法逃离局部极值、避免早熟收敛等方面有较好的测试能力。函数的维数越高,运算复杂度越大,因而选用高维函数可以验证智能算法的寻优性能是否足够好。本文所选标准测试函数如表1所示。
3.2 仿真实验结果及分析
为了验证本文算法的有效性和可行性[17-18],将EBSA与5种经典的群体智能优化算法(包括基本鸟群算法)分别在标准测试函数上进行多次测试。由于不同文献对智能优化算法进行有效性测试时采用的测试参数有差别[3-9],本文在通用参数设置相同的基础上,对各个优化算法的参数采用参考文献中的默认设置。设最大迭代次数M=1 000,种群规模(初始鸟群、粒子群、鱼群等)N=30。粒子群算法(PSO)、人工鱼群算法(AFSA)、布谷鸟搜索算法(CS)、蝙蝠算法(BA)、鸟群算法(BSA)的其余参数设置如表2所示。

表1 标准测试函数Table 1 Standard test function
为了实验的准确性,对6种智能优化算法按表1所示9个典型测试函数分别进行50次独立实验。仿真实验环境为:运行内存8 GB,Win7 64位操作系统,Matlab R2016a。评价指标里的BEST,MEAN,WORST,STD,SR值分别代表50次试验中结果的最优值、平均值、最差值、标准差以及寻优成功率(寻优差小于10-5认定为寻优成功)。实验仿真结果如表3所示。由表3可知:对于函数f1,f2,6种智能优化算法具有良好的寻优能力,即都能够找到全局最优解,而BSA和EBSA拥有比其他算法更好的寻优效果,它们的最优值BEST、最差值WORST、平均值MEAN、标准差STD都比其他6种算法提升了一个数量级。对于函数f3~f5,只有BSA和EBSA能准确找到函数最优值,可见具有较理想的寻优结果,而其他4种算法的寻优率并不理想。对于复杂函数f6~f9,基本鸟群算法拥有良好的最优值BEST,但其最差值WORST、平均值MEAN、标准差STD和寻优成功率SR较差,表明其在寻优计算中易陷入局部极值从而影响算法整体寻优性能。而高效鸟群优化算法在最优值BEST,最差值WORST、平均值MEAN、标准差STD和寻优成功率SR这五个指标都表现出了优异的效果,寻优成功率提高10%左右。为了更加明显地体现高效鸟群优化算法对复杂函数的收敛效果,画出6种智能优化算法对于9个测试函数达到收敛时的平均迭代次数条形对比图,如图1所示,图中收敛次数置顶说明该算法对目标函数的收敛成功率为0。从1图中可以看出对于复杂函数,EBSA达到收敛时的迭代次数较BSA有了明显的提升,基本上可以达到原始鸟群算法次数的50%。综上可知,改进的EBSA对不同类型的单峰/多峰、低维/高维、可分/不可分测试函数具有较好的寻优能力,比原鸟群算法拥有更好的寻优能力和收敛速度,尤其是在较复杂函数寻优时较好地避免了早熟收敛、落入局部极值点。
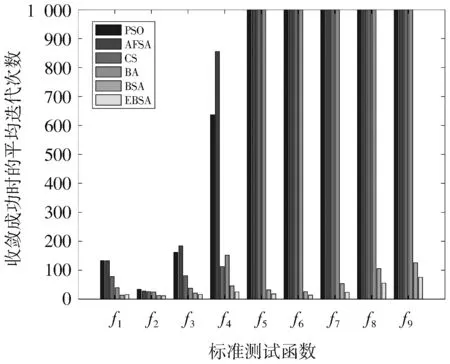
图1 六种算法针对9个标准测试函数的迭代次数图Fig.1 Diagram of iteration times of six algorithms for nine standard test functions

表2 智能优化算法参数设置Table 2 Parameter setting of intelligent optimization algorithm
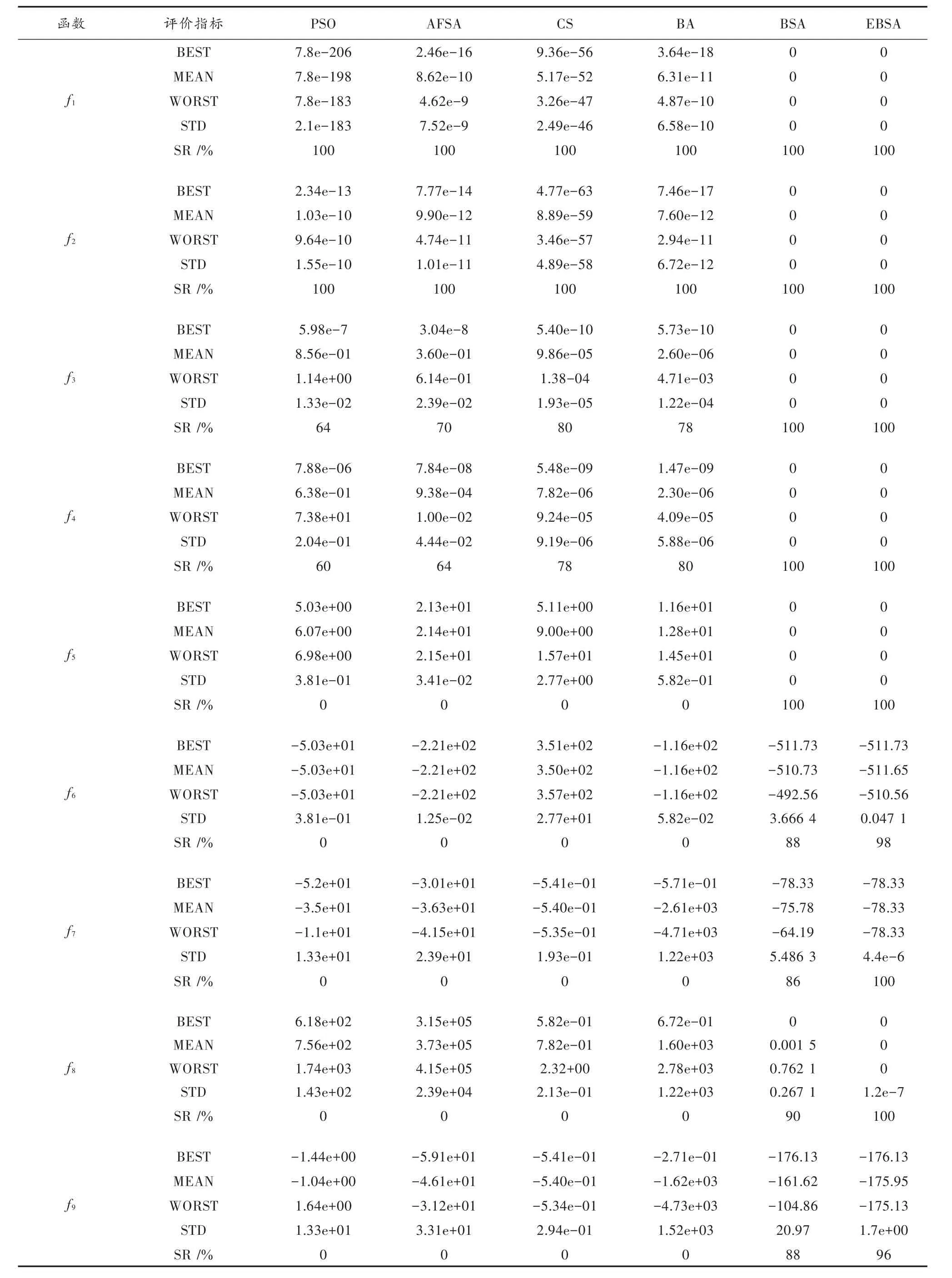
表3 不同智能算法之间的性能比较Table 3 Performance comparison of different intelligent algorithms
4 结 语
为了提高鸟群算法在群智能进化过程中的寻优特性,本文在BSA中加入挑食行为、智能学习行为,提高算法寻优的能力;同时将双高斯函数引入鸟群更新行为,人为干预寻优空间内鸟群的多样性,构建双高斯函数更新行为,进一步提高算法在求解复杂函数时的全局寻优性能,较好避免了算法早熟而陷入局部极值。
对具备不同测试特性(单峰/多峰、低维/高维、可分/不可分)的9个典型标准函数进行寻优仿真。仿真结果表明,本文提出的EBSA的收敛性能和寻优能力均优于(或针对部分测试函数不亚于)BSA,PSO,AFSA,CS,BA等群体智能优化算法,尤其在对复杂度更高的函数进行寻优仿真时,收敛速度和收敛精度远远优于其他几种智能算法,并有效提高了鸟群算法的全局寻优性能。
