一种频率约束的高效用模式挖掘算法

张全贵 曹 阳 李志强

(辽宁工程技术大学电子与信息工程学院 辽宁 葫芦岛 125105)

0 引 言

传统的频繁模式挖掘只考虑项在事务中是否出现[1-3]，而忽略了项本身所拥有的效用信息。如:商场中钻石和牛奶的效用信息差距较大，二者不能同等对待。因此，基于支持度的频繁模式挖掘已很难适用于实际问题。从而高效用项目集挖掘方法得到更多的重视[4-8]。效用模式将赋予每个项不同的权重并且同一项可以在各个事务中重复出现，这更符合现实社会的供应和需求。

虽然基于效用的框架大大增强了所得模式的实用性[9]，但是当效用被认为是选择模式的唯一指标时，挖掘出来的项集有可能是低频的，这往往对商家并没有太大意义。例如，在商场中，钻石的利润比普通银饰高得多，但其销量要远低于普通银饰。传统的高效用模式挖掘可能认为销售钻石是高效用的模式，但是从实际营销来看，如果很长时间才卖出一件商品，虽然利润很高，但是从长远的角度来看对商家并不一定有太大好处。在现实生活中，仅仅关注单件商品的利润是不够的，顾客购买的商品频率对商家来说也很重要。商家要将两者综合考虑来对商品进行摆放和管理。

因此本文提出了一个新的高效用模式挖掘算法，目的是将一些频繁出现的，但因为效用值偏低而被传统的高效用模式过滤掉的模式挖掘出来。这样在零售业的经营中，可以帮助零售商和店主发现最有利可图的产品或产品组合，以便更好地建立能够获得高利润的营销策略。

1 相关工作

目前，已经有很多算法对高效用模式挖掘进行了研究。文献[10]在2004年第一次引入了高效用模式挖掘的概念。随后，文献[11]提出了Two-Phase算法，并且提出了TWU(Transaction weighted utilization)模型。该算法通过层次的方式产生候选项，需要对数据集进行多次扫描，时间和空间的代价较大。文献[12]提出IHUP算法，其在增量数据库中挖掘高效用模式，采用模式增长的方式生成候选项集，虽然没有多次重复扫描数据库，但候选模式的数量还是很多。为了克服这个问题，文献[13]提出的UP-Growth算法针对建树的方法给出了改进策略，减少了候选项的数目，算法的时间效率得以提高。

然而，现有的高效用模式挖掘算法[14-16]都不适用于解决本文提出的问题。因此，本文针对UP-Growth算法进行改进，提出了一种频率约束的高效用模式挖掘算法。通过同时考虑频率因素和效用因素，对高效用模式的定义和事务加权效用值的计算公式进行了修改，以便能挖掘出更为高效的模式。并通过优化策略，缩小候选项集，提升高效用模式的生成效率。

2 问题定义

给定的I={i1,i2,…,im}是数据库中的项集。设D={T1,T2,…,Tn}为包含n个事务项集。每个事务Tc∈D是由I中的项目组成。每个项ik∈I(1≤k≤m)都包含内部效用和外部效用，内部效用是指项目的数量，记作q(ik,Tc)∈(1,2,3,…)。外部效用是指项目的单位效用，记作p(ik)。在数据集D中可以用|D|表示事务的个数。表1给出的是数据集片段，表2是效用表。

表1 数据集片段

表2 效用表

定义1项目ik在事务Tc中的效用值u(ik,Tc)为:

u(ik,Tc)=p(ik)×q(ik,Tc)

(1)

定义2项集X在事务Tc中的效用值u(X,Tc)为:

(2)

定义3项集X在整个数据库D中的效用值u(X)为:

(3)

定义4一个事务Tc的事务效用值TU(Tc)为:

(4)

定义5在一个事务数据库中，一个项集X的频数是项集X在数据库中出现的次数，表示为SN(X)。

项集X的频率SUP(X)为:

(5)

定义6高效用项集是指项集的效用值乘以项集的频率不低于用户指定的最小效用阈值(记作min_uti)的项目集，找到这些项目集就是高效用模式挖掘的目标。

定义7一个项集X的事务权重效用值TWU(X)为：

(6)

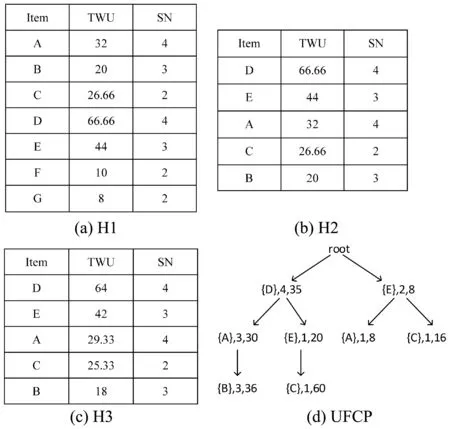
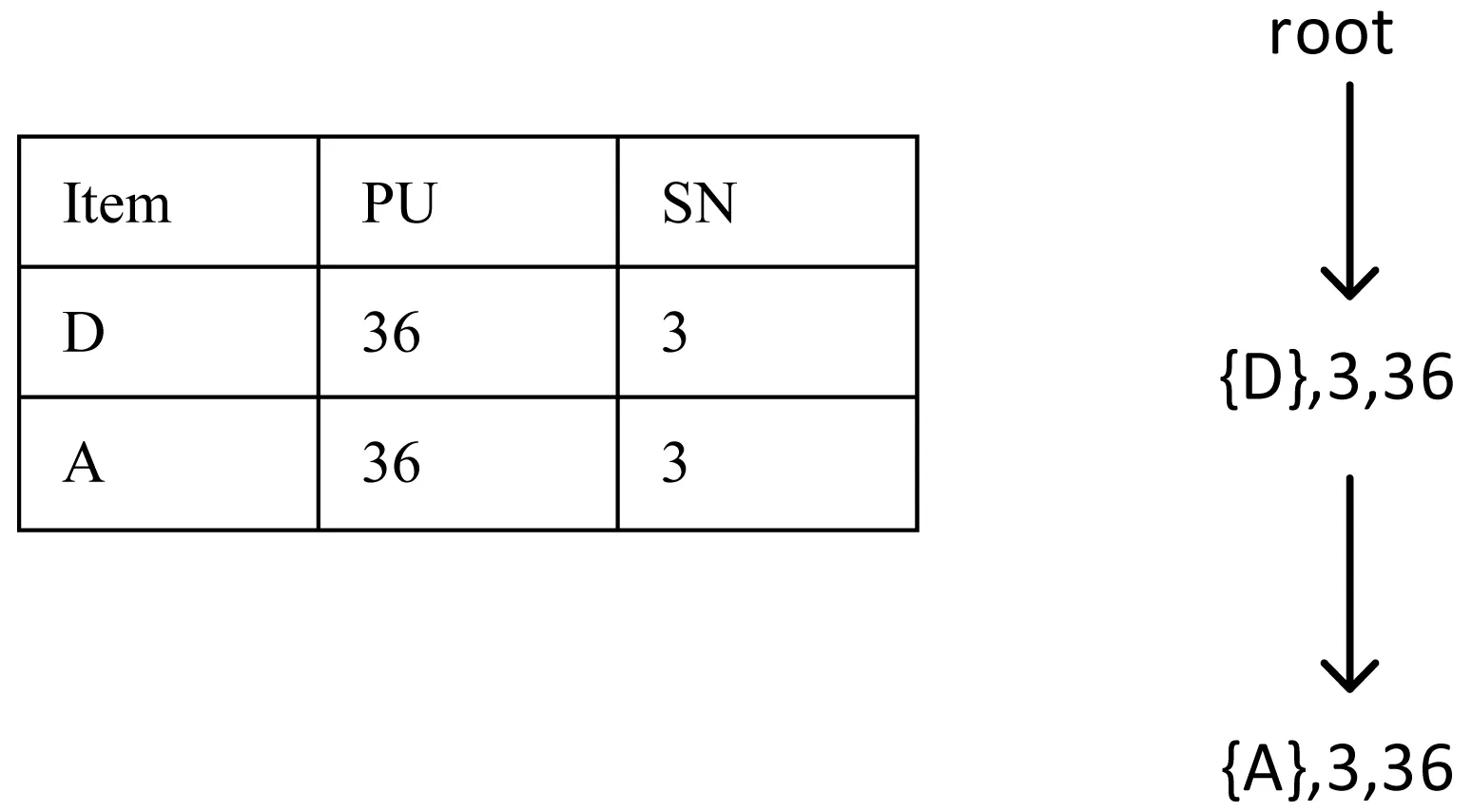
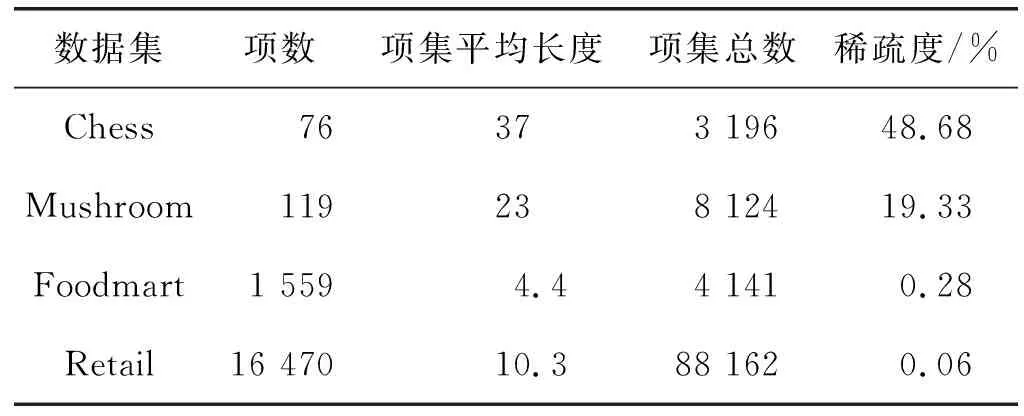
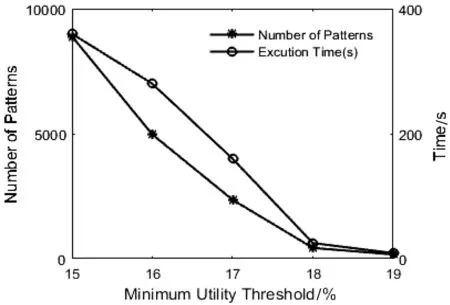
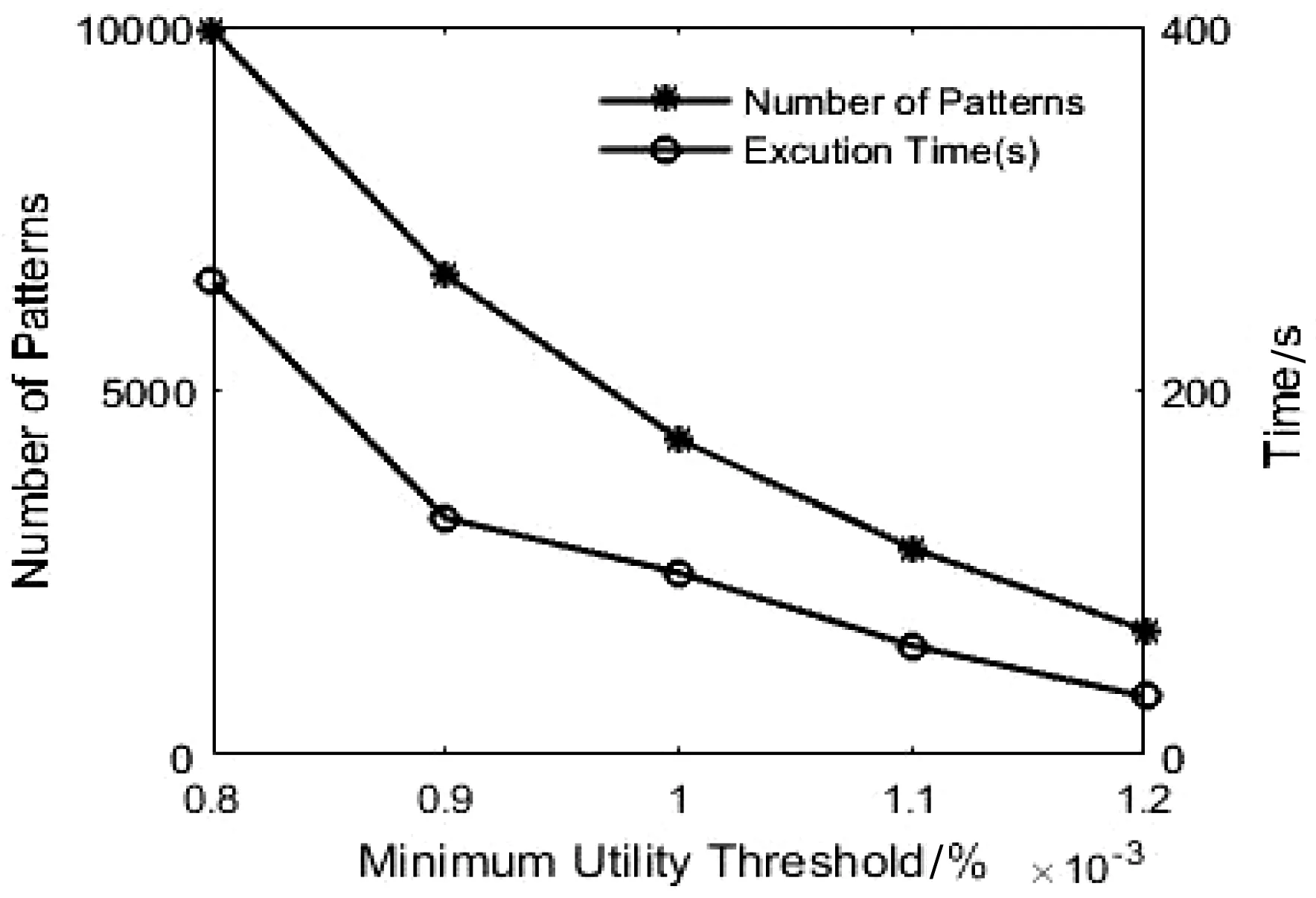
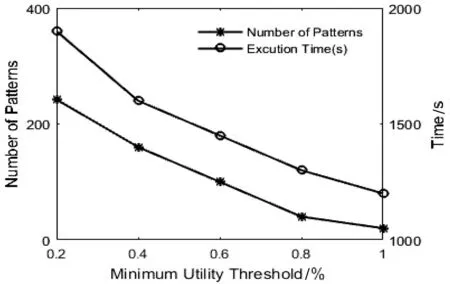
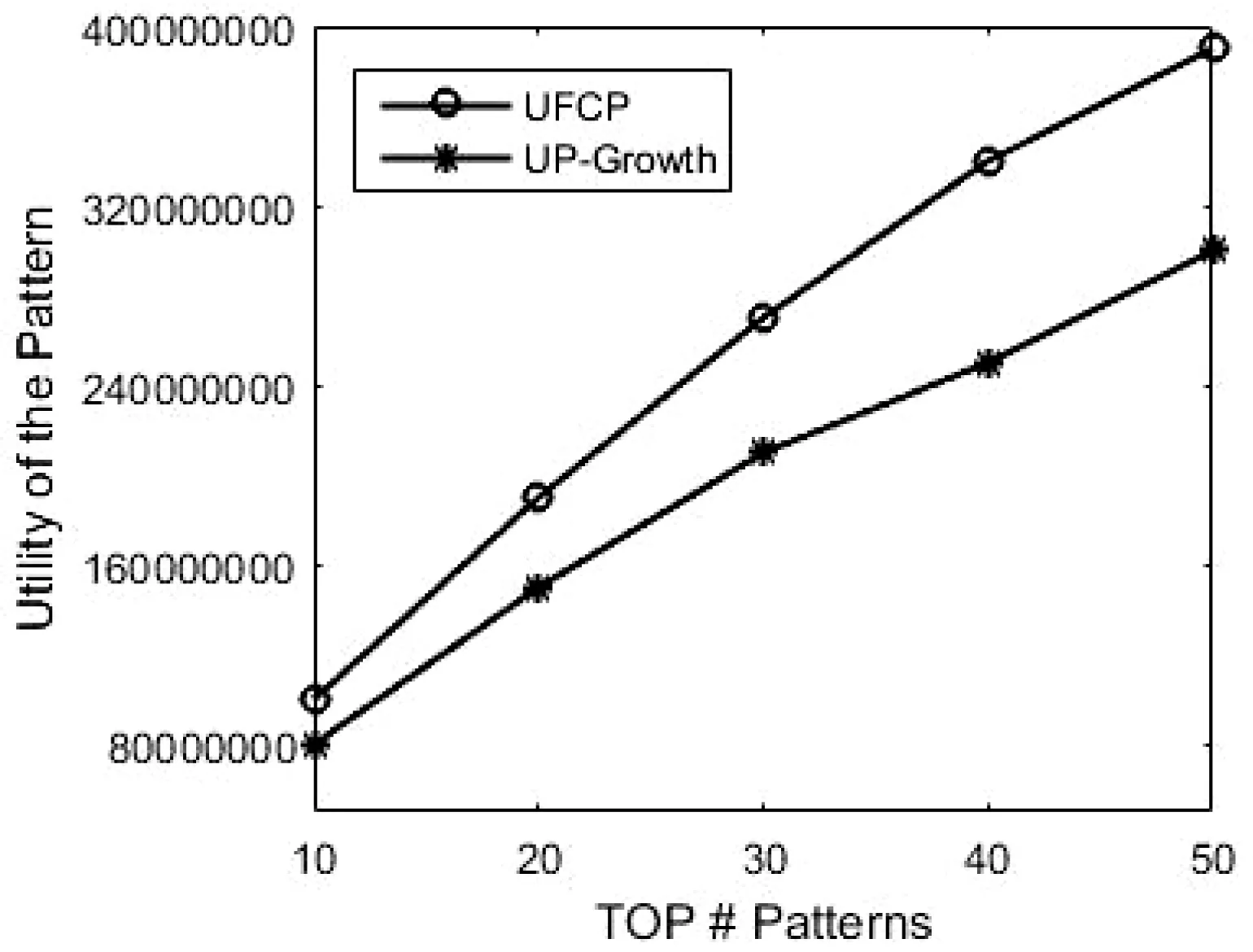
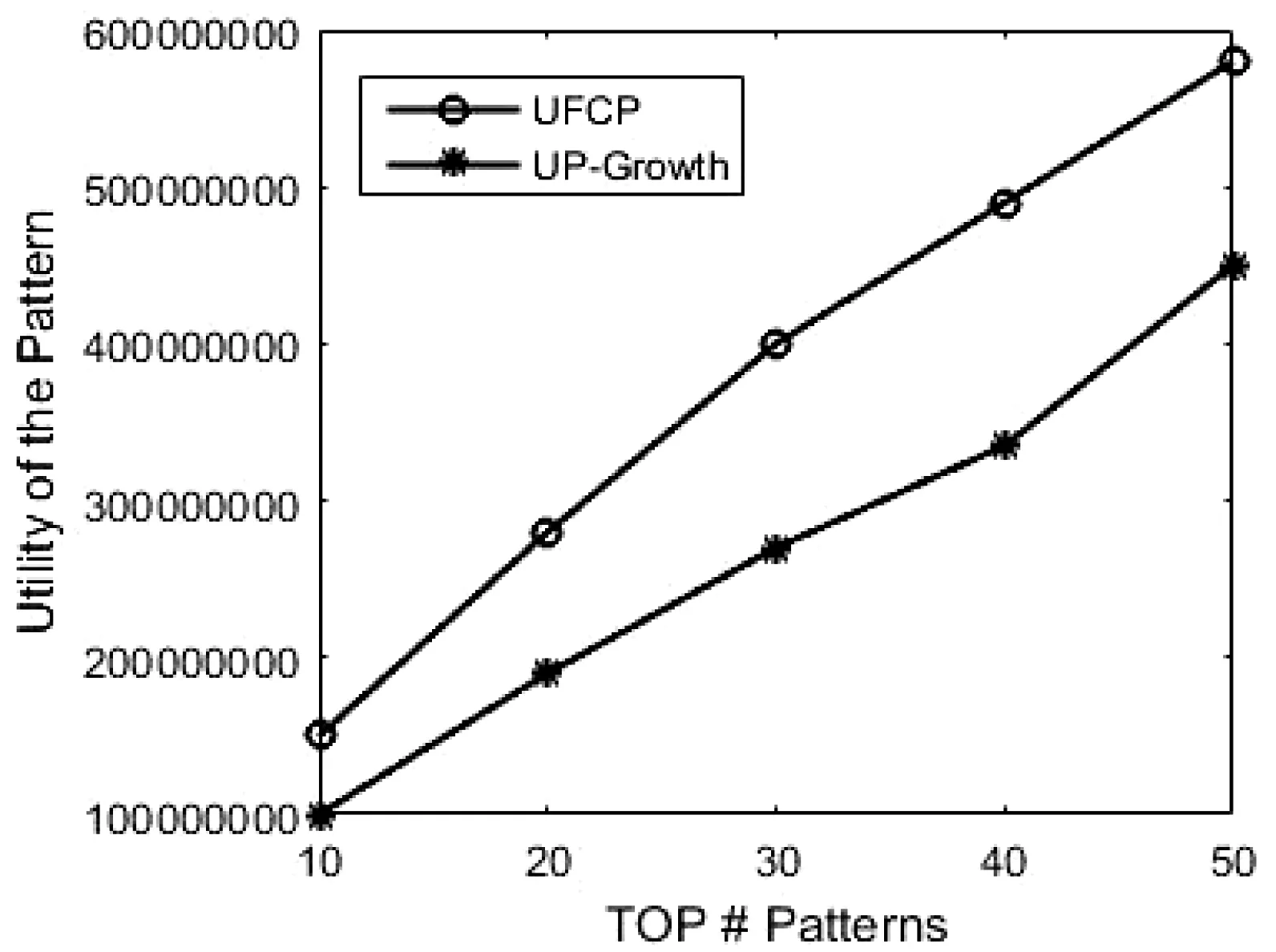
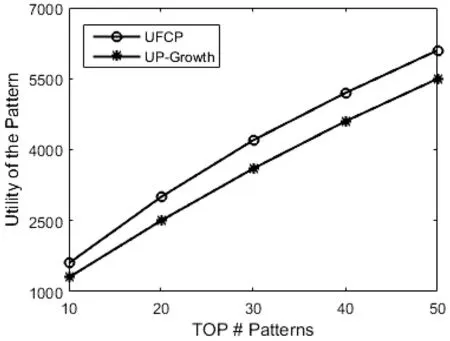
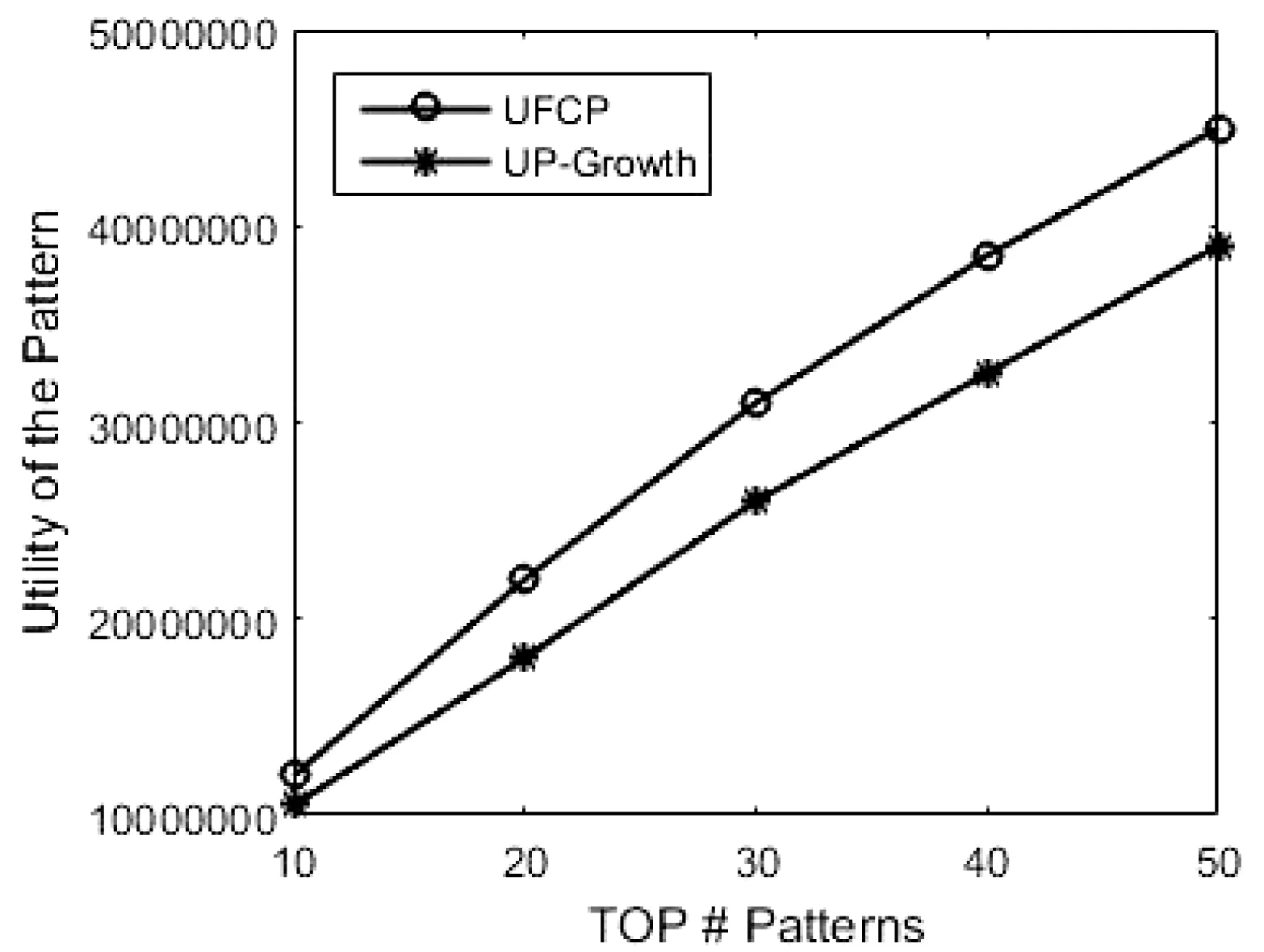
定义8若TWU(X)≥min_uti，X是候选项集；若TWU(X)

定义9如果不存在u(ik,Tc′)>u(ik,Tc)的事务Tc′，那么项目ik在交易Tc中的效用被称为项目的最大效用max(uik)。

性质1项集的事务权重效用值TWU符合闭包属性[10]:如果某个项集是候选项集，那么其非空子集也是一个候选项集；如果某个项集是非候选项集，那么其超集也是一个非候选项集。

性质2同一个项目在不同事务中的效用可能是不同的，因为需要考虑到每一个项目数量。

例如，在表1中，假设给定的最小效用阈值是50，传统的高效用模式会将交易T4中的项集挖掘出来，而其他项集会被过滤掉。然而，在本文定义的高效用模式中，因为项集{CDE}在整个数据集中只出现一次，所以u(CDE)=60×1/6=10，而项集{ABD}在数据库中出现3次，u(ABD)=(16+8+12) ×3/6=18。假设将最小效用阈值设置为15，{ABD}是一种高效用模式。

3 UFCP-Miner算法

本文提出的算法是基于UP-Growth算法进行改进的，将改进后的算法记为UFCP-Miner算法。由于UFCP-Miner算法将频率因素和效用因素同时考虑进高效用模式挖掘中，因此在创建UFCP-Tree的过程中，通过第一次扫描数据集，按照定义5给出的公式计算每项出现的频数及其频率，在计算TWU时，根据定义7将项目频率和效用值相乘。这样可以将传统算法挖掘出来的低频高效用模式直接过滤掉。并且在高效用模式的判断过程中，重新计算真实效用值和频率的乘积，这样也保证了结果的准确性。此外，算法在产生候选项集的过程中，通过对项目最大效用值的计算，可以直接排除一些非候选项,以提高算法的性能。UFCP-Miner算法按三个步骤来执行：

(1) 通过两次扫描数据集计算效用值，并将事务项集整理到UFCP-Tree上。

(2) 通过创建条件模式基依次从UFCP-Tree中找到候选项目集。

(3) 从得到的候选项目集中判断哪些是高效用项目集。

3.1 创建UFCP-Tree

算法采用树结构来保存项目集的所有信息。通过一个头表来实现树的遍历。节点的第一个位置存储的是项目名，第二个数代表项目对应的频数，第三个数代表项目对应的效用值。创建UFCP-Tree的过程算法如下：

算法1

输入：事务数据库D；

用户最小效用阈值min_uti。

输出：UFCP-Tree。

1) 扫描D中所有事务，计算每项的SN，SUP，TWU;

2)forD中的每个事务Tcdo;

3)forTc中的每个项ikdo;

4)If(twu≤min_uti)then;

5) 删除该项;

6)Endfor

7)Endfor

8) 对Tc中剩余项按TWU值降序排序;

9) 将D中不在头表中的项删除;

10) 将D中保留下来的项按表中的顺序进行排序;

11) 重新计算每项的TWU值;

12) 将事务项集按顺序添加到UFCP-Tree上;

13)End

例如，本文以表1和表2中列出的数据为例, 这里设定15为最小阈值。通过第一次扫描数据集，结果如图1(a)所示。因为F、G的TWU值小于15，所以，F、G被删除。排序后的结果如图1(b)所示。删除不在H1中的项，重组后的事务如表3所示。图1(c)给出了重新计算后的TWU值。然后将表3中的事务依次添加到UFCP-Tree上，如图1(d)所示。

图1 UFCP-Tree的构建

表3 重组的数据集

在扫描数据集的过程中，UFCP-Miner算法还计算了各项在数据库中的最大效用值[17]，如表4所示。

表4 项最大效用表

3.2 产生候选项集

创建好UFCP-Tree之后，就是如何产生候选高效用项目集。算法首先从头表底部开始依次处理每一项,若其估计效用值高于min_util，为项目创建条件模式基，并为当前条件模式基创建子头表。根据子头表中的数据，为其创建条件效用子树，然后统计每一项的最大效用，若最大效用小于假定的最小效用阈值，该项就不是一个候选项集[17]，同时删除子头表中小于最小效用阈值的项。最后按顺序依次处理子头表中的所有项，直到挖掘出全部候选项集。算法如下：

算法2

Input: A UFCP-TreeTx, a header tableHxforTxand an itemsetX

Output: All PHUIs inTx

ProcedureUFCP(Tx,Hx,X)

1)ForeachitemikinHxdo

2)Foreachentrynjfor the itemikinTxdo

3) estimate utility+=nj.utility;

4)Endfor

5)If(estimate utility≥min_uti)then

6) Generate a PHUIY=X∪ik;

7) Construct Y’s conditional pattern base Y-CPB;

8) Calculated Y’s maximum utility according to maximum item utility table

9) Remove unpromising items inHy;

10)IfTy≠nullthencallUFCP(Ty,Hy,Y);

11)Endfor

例如，根据图1(c)，首先考虑项{B},由于其估计效用值(即36)高于min_uti，因此为B创建条件模式基。B的最大效用是将项目B的最大效用值乘以项目B的频数，再乘以项目B的频率，即3×3×0.5=4.5，由于4.5<15，则{B}不是一个候选项集。通过扫描UFCP-Tree上节点“B”到根节点路径上的所有项，一条路径{B-A-D}被发现，计算出每项的路径效用，即重组的数据集中包含项集(BAD)的事务效用和，记为PU。为了方便起见，因为每条路径中都必须包含“B”，所以表中只保存除了“B”以外的其余项。如图2所示。最终可以得到和项“B”相关的候选项集有{BA}{BD}{BAD}。

图2 子头表和子树的构建

3.3 得到高效用模式

第三次扫描数据库，将所有候选项集的真实效用值统计出来，并将其与项集的频率相乘，若结果大于给定的最小效用阈值，该项集就是高效用项集。

4 实 验

4.1 实验介绍

为了检验算法的性能，本文将提出的算法和经典的UP-Growth算法进行了对比分析。实验采用的系统是64位的Windows 7，内存为4 GB，处理器Intel Core i5-2450M CPU 2.50 GHz，算法是由Python语言编程实现。

实验采用四个典型数据集对算法进行实验分析，表5列出了各个数据集的参数。由于所选数据集都不包含项的内部及外部效用值, 因此采用文献[18-19]中的方法，每个事务中项目的个数由1到5随机生成，项目的单位效用值由1到1 000随机生成。由于在现实生活中，相对来说单位效用值高的项目较少，这里随机产生的单位效用值的数量服从对数正态分布。为了确保实验结果的客观性，每个实验结果都是采用运行多次取其平均值的方法。

表5 数据集特征

4.2 实验结果分析

图3给出了在四个不同的数据集上，通过设置不同的最小效用阈值，挖掘出高效用模式的数量和运行时间。很明显随着最小效用阈值的提高，候选项的数量随之变少，因此需要更少的运行时间。在图3(a)的实验中，当阈值从30%提高到35%的时候，算法的运行时间会急剧减少，这是因为随着阈值变化生成的候选项数量明显变少，所以在最后判断时只需要计算少量的项集频率。而在稀疏数据集Foodmart上进行测试时，如图3(c)所示，随着阈值的提高候选项数量也在减少，但时间增长的相对平稳，主要是因为该Foodmart中事务项集平均长度只有4.4，所以计算候选项集的频率的时间会远少于事务项集平均长度较长的数据集。因此，算法的运行时间变化相对平缓。

(a) Chess

(b) Mushroom

(c) Foodmart

(d) Retail图3 运行时间和候选项数量

因为本文是为了挖掘出更高效用的项集而重新定义了高效用模式，所以将提出的算法和经典的高效用挖掘算法UP-Growth在挖掘结果的效用值上进行了对比分析。首先将UP-Growth算法挖掘出来的高效用项集与项集对应的频率相乘，然后取两种算法挖掘结果的前10、20、30、40、50个模式的效用和在两个稀疏和两个稠密数据集上进行对比，如图4所示。由图可以很明显看出，提出的算法和UP-Growth算法在所得模式的效用值上有较大差异，并且数据越稠密，项集平均长度越大，差异越明显。主要是因为UP-Growth算法挖掘出来的模式可能是低频的，所以乘以频率之后结果要小于UFCP算法得到的结果。UFCP算法挖掘出的结果是具有高频率的高效用模式，使最终结果会优于UP-Growth算法。此外，随着模式的增多，效用值差距也会变大。

(a) Chess

(b) Mushroom

(c) Foodmart

(d) Retail图4 模式的效用

综上所述，UFCP-Miner算法在传统高效用模式的基础上加入频率因素，从而获得更为高效的模式。此外，在产生候选项集的过程中，通过优化算法，过滤掉了一些非候选项集，使得运行时间相对减少。但UFCP-Miner算法在计算项集频率时仍会消耗一定的时间。

5 结 语

本文通过对现有高效用模式挖掘算法的分析，提出了一种频率约束的高效用模式挖掘算法。基于实际问题重新定义了高效用模式，在挖掘过程中考虑项集在整个数据库中出现的频率，将那些出现频率较高但因效用值偏低而被过滤的模式挖掘出来并过滤掉低频的模式。实验采用4个典型数据集，实验结果也证明了本文提出的算法在挖掘结果上不同于传统的高效用模式挖掘，这样的挖掘结果对商家来说更有意义。未来的工作是进一步优化算法的时间复杂度，并将此算法迁移到高效用序列模式挖掘领域。