一种基于分块主成分分析的存储器容错方法研究

方嘉言 邵翠萍 李慧云

1(中国科学院深圳先进技术研究院 深圳 518055)

2(西安电子科技大学 西安 710071)

1 引 言

自集成电路问世以来，该行业就一直按照摩尔定律以一种惊人的速度发展着。随着集成电路工艺水平的飞速进步，深亚微米时代已经到来，集成电路的规模越来越大，密度也越来越高[1]。同样，存储器内部存储单元的尺寸也越来越小，存储单元的密度随之增加。这使得存储单元更易受到温度、电磁干扰、辐射等影响而发生参数变化和软错误等故障[2]，从而严重威胁器件功能的正确性，很可能会对生产、生活造成严重的影响。

随着信息社会产生的数据量呈现爆炸性增长，人们对可靠且大容量存储系统的需求也在急剧增加[1]。截至 2017 年，部分芯片内部存储器占据了约 70% 的面积，这将进一步增加发生故障的概率[3]。

为了保持存储设备中数据的正确性，国内外目前常用纠错码(Error Correcting Code，ECC)[4]，如 Hamming 码(汉明码)和低密度奇偶校验码(Low Density Parity Check Code，LDPC)作为纠正故障的手段。卜雷雷[5]采用扩展汉明码和三模冗余结合的纠错检错方式，实现了一种可以选择检纠错模式的星上随机存储器。与原有经典设计相比，该设计增加了修正数据的回写功能，并且在应用上具有较好的灵活性。但是，在存储单元的尺寸越来越小，存储器中数据位数不断增加的前提下，实现“纠一检二”功能的 Hamming 码不再能满足增长的对纠错能力需求。王方雨等[6]将里所码(Reed-Solomon Codes，RS)应用于闪存存储器中，该设计在其相机项目中很好地保护了存储器的数据，但需要经过复杂的计算，影响数据保护效率。Lee 等[7]采用非对称的密度演化来优化 LDPC 码，显著降低了 LDPC 编解码过程的复杂度，但对硬件资源的消耗并没有得到显著降低。许志宏等[8]将 RS 码和 LDPC 码结合应用于星上存储器，采用扩展校验码的方式增强了 RS码的纠错能力，并通过改变编码方式在一定程度上减少了 LDPC 码的资源消耗，但对硬件资源消耗过大的问题并没有得到解决，而且还增加了执行时间。

为了限制硬件资源的消耗，许多应用都采用了近似容错的方法，并放宽了对数据 100% 精确的限制[9]，如近似计算等领域。张罡和董朝领[10]针对目前标准蒸发器环形管板设计计算没有统一标准的情况，提出了一种用于环形管板厚度的近似计算方法。与 SW6-2011 软件的计算结果相比，该方法得到的结果更加安全可靠。Venkataramani 等[11]提出了一种用于近似计算的可编程平台，该平台显著提高了处理数据的效率。

本文以数据块为单位，采用主成分分析(Principal Component Analysis，PCA)方法对原始数据进行特征提取，并将得到的不同块的特征作平均，获得一个平均的特征数据，然后采用该平均特征数据作重构恢复，最后将重构的块结果作为原始数据的近似估计。当检测到原始块中数据发生故障时，可用这个近似估计矩阵的相应位去替换块中的故障数据，达到对原始数据容错保护的目的。该方法的优点是：首先，采用分块 PCA极大程度地降低了算法复杂度，减少了算法运行时间；其次，利用分块 PCA 作特征提取能够有效地保留数据的局部特征[12]，进而提升原始数据重构的精度；最后，采用重构的子块仅对原始数据中的故障数据作容错替换，能够极大地保留原始数据的精度。该方法利用数据的特征对数据进行容错，能够对块数据中的单比特位或者多比特位的翻转故障进行容错纠正[9]。与现在普遍使用的 ECC 方法相比，该方法不需要增加硬件开销，所需的执行时间和消耗的内存都较少。

本文内容组织如下：第 2 部分介绍了主成分分析和现有容错方法的背景；第 3 部分具体阐述了基于分块主成分分析的存储器容错技术；第 4部分对所提出的容错技术进行实验验证；第 5 部分将本文结果与国内外相似研究进行对比分析；第 6 部分总结。

2 背 景

2.1 主成分分析

PCA 是一种基于 Karhunen-Loeve 变换的统计分析方法，是寻求有效的线性变换的经典方法之一。它的原理是使高维数据通过一个特殊的特征向量矩阵投影到一个低维空间，从而达到数据降维的目的，并且能够消除数据之间的相关性。其中，所用到的特征向量是一个低维向量矩阵，通过高维数据投影后的低维表示和特征向量矩阵，可以近似重构出该高维数据[12]。

主成分分析算法的降维步骤如下[13]。设原始高维数据X的尺寸为m×n，用向量可表示为[x1,x2, …,xn]。其中，每个列向量中包含m个元素。

首先，对于矩阵X中的所有列向量作中心化处理，使其平均值等于 0。均值中心化处理后，使用矩阵X来计算协方差矩阵S。然后，求取协方差矩阵S的特征值λ1,λ2, …,λn和特征向量v1,v2, …,vn。最后，将这些特征值从大到小依次排列后，按照贡献率选取所需的主元。

设Vk是S中前k个主元所对应的特征向量矩阵，经过中心化处理的数据X在特征空间中的投影Y可由公式(1)得到。

通过投影Y可以重构出原始数据，重构公式如下：

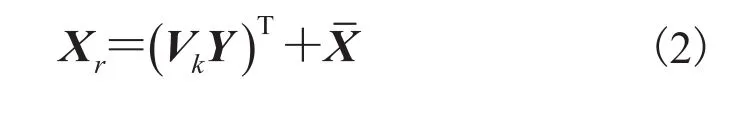
2.2 现有容错加固技术

随着存储芯片容量的增大，器件的成品率呈指数规律下降。通常人们一方面从工艺角度入手，改良制造工艺以提高成品率；另一方面从设计角度入手，如电路级、门级和系统级，在电路设计时通过增加冗余的方式来实现可靠性的提高。这些方法都是为了从不同角度入手达到降低故障发生率、修复已发生故障的目的。具体的技术有：基于工艺级容错加固技术、基于版图级容错加固技术、基于电路级容错加固技术、基于系统级容错加固技术和基于软件级容错加固技术[14]。

(1)基于工艺级容错加固技术

工艺级容错加固技术是指在集成电路的生产制造过程中，使用特殊的工艺技术来降低故障的发生率。采用的主要技术是绝缘体上硅(Silicon On Insulator，SOI)技术。采用 SOI 工艺制造的集成电路具有寄生电容小、短沟道效应小、速度快、集成度高、抗辐射能力强等优点，但其生产制造成本要远高于互补金属氧化物半导体工艺。虽然工艺级加固技术可以很好地提高存储器抗单粒子翻转的能力，但由于需要使用特殊的工艺技术改进生产线，提高了生产成本。

(2)基于版图级容错加固技术

版图级加固技术是指通过调整电路的版图结构、隔离或者重排列晶体管等方式，抑制电路中敏感节点的软错误。版图加固技术主要基于隔离、源漏扩展、版图优化和脉冲窄化等。保护环和保护漏是最典型的两种隔离技术，这两种方式分别在 P 型金属氧化物半导体和 N 型金属氧化物半导体上增加冗余结构，防止了敏感节点的电荷收集，能够很好地抑制单粒子翻转对晶体管的影响。版图级加固需要对已有版图设计增加冗余，改变布局结构，重新进行布局布线，增加了后端设计的工作量。

(3)基于电路级容错加固技术

电路级容错加固技术是指采用特殊的电路结构，以提高电路抵制各种类型瞬态故障的能力。其中，静态随机存取存储器、寄存器、锁存器等基本单元及组合逻辑门的容错属于电路级加固的研究热点。一般是在原有电路的基础之上，不改变电路的功能，通过优化电路结构、改变电路连接方式或者插入冗余部分来实现对故障的预防。该种加固技术的容错单元需要进行全定制设计，增加了生产制造的时间和成本，不利于该技术的应用和实现。

(4)基于系统级容错加固技术

系统级加固技术是指通过信息冗余的方式，检测并修正已发生的故障来提高电路对故障的抵制能力。存储器采用纠错编码的方式，自动检测并纠正故障，是提高存储芯片成品率和可靠性的有效措施[15]。常用的检纠错码有奇偶校验码、汉明码及其改进码、RS 码和 LDPC 码。系统级容错加固技术极大地提高了存储器的可靠性，而且并不需要在工艺流程或设计方法上作任何改变，是比较常用的保护存储器的方法。但该方法纠错性能受限，并且也占据了较多的面积、消耗了很高的功耗和执行时间[16]。

(5)基于软件级容错加固技术

软件级加固技术是指采用软件的方式，检测并纠正存储器中的故障数据，提高存储器的可靠性。软件级的方法根据数据类型的不同，主要分为两类：一类是通过重复或并行执行从存储器中读出的程序数据，并对结果进行比较，以检测数据中是否存在故障；另一类是基于算法的方式，通过相应的容错算法得到计算结果，并和预留参考信息对比，实现故障的检测和纠正[14]。软件级的容错技术，能够充分利用现代计算机多处理器的硬件资源，配置方便，对硬件没有特殊要求，成本低，应用范围广。

综上所述，工艺级容错加固技术需要改变现有工艺技术，提高了生产成本和生产周期。版图级容错加固技术需要对电路结构作出调整，重新进行布局布线，增加了后端设计的难度。电路级容错加固技术需要采用新的设计单元，增加了生产成本，不利于技术推广。系统级容错加固技术虽然不用在设计上或工艺流程上做出改变，较前几种方法具有较大优势，但该方法需要消耗较大的硬件资源，执行时间长。而本文采用分块主成分分析的容错方法，是基于软件级的容错加固技术，不用改变工艺技术或现有设计，利用数据的特征对其作容错保护，可以纠正多比特位翻转的故障，硬件资源开销小，算法的可移植性强。

3 基于分块主成分分析的存储器容错方法

本文提出的基于分块 PCA 的存储器容错方法是基于软件级的，容错方法如图 1 所示。

3.1 生成校验位

在故障检测模块中，对于m×n维的原始数据X，每一个数据都是 32 位的，本文对每个 32位数据都产生 1 位的奇偶校验位，得到校验位矩阵Xpar。该方法能够很好地检测到数据发生奇数个比特位翻转故障的情况。原始数据X产生奇偶校验位的方法如图 2 所示。其中，xij(0＜i＜m，0＜j＜n)代表X中的具体数据；Pij代表xij对应的奇偶校验位。

图1 基于分块主成分分析的存储容错方法Fig. 1 Fault-tolerant method based on modular principal component analysis

图2 数据校验位产生方法Fig. 2 Parity bit generation method for data

3.2 特征提取

分块 PCA 是在 PCA 的基础上，对需提取特征的数据进行分块预处理：先将其等尺寸分割为若干子块数据，然后对这些子块数据分别应用PCA 进行数据降维和数据重构。该方法既能在降维过程中很好地提取原始矩阵数据的局部特征[17]，又能加快图像的降维和重构，减少硬件资源的消耗。与 PCA 相比，分块 PCA 重构出的数据质量较高[18]。

分块 PCA 对于所分子块数据的尺寸是敏感的。如果子块数据的样本维数较高，则会增加数据的降维时间；如果子块数据的样本个数较多，那么会增加数据的重构时间，最终导致分块 PCA的整体总降维或总重构时间增加，这是由 PCA算法的属性决定的。

分块 PCA 的总执行时间主要受子块数据维数高低的影响，数据维数越高，执行时间越长。但如果维数过小，随着子块数据数目的增多，执行时间反而会增加。这是由于此时子块数目增加对执行时间的影响超过维数降低对执行时间的影响所致。并且，当分割维数过小时，降维获得的主元数目也会很少，实验中可用的结果就会变少。所以分块数据的维数一般选择较小的数，如4 维或 8 维，这样既可以控制执行时间，又可以得到较多的实验结果。在占用内存差距不大的情况下，保留同样比例主元时，重构数据的质量与子块数据的维数成正比；而子块数据样本个数为了简便，选为原数据的一半即可。

对于原始数据为X，分块 PCA 的具体实现方法如下：首先，对于需要做降维处理的原始数据X，将其等尺寸分割为p×q个r×c维的小尺寸数据。其中，p×q＝m，p×c＝n。然后，对位于X中的第一块r×c维的数据x1应用 PCA 进行降维，提取该块数据的特征，得到块降维结果y、块特征向量矩阵vk和块均值距阵。最后，按照前述方法依次实现对X中其余子块数据的降维，并得到这些降维数据各自块的y、vk、

分块 PCA 实现对X中的任意块数据xi的降维过程如图 3 所示。

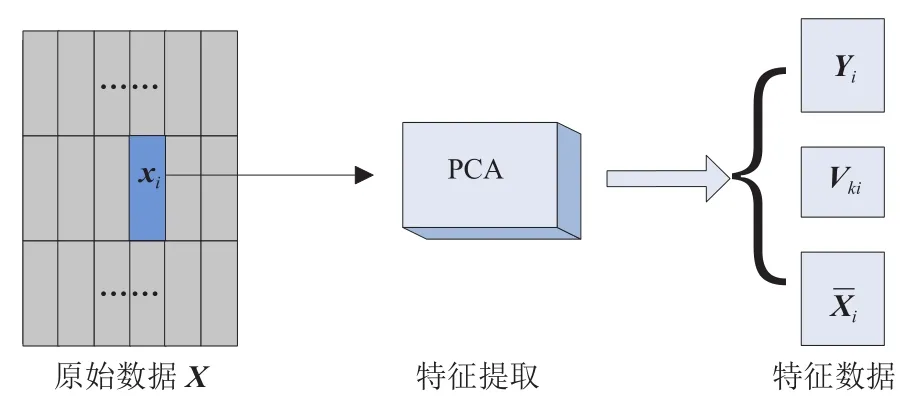
图3 分块主成分分析的降维过程Fig. 3 Dimension reduction process of modular principal component analysis

3.3 容错块计算

容错块即最佳估计矩阵，就是当校验位检测到故障时，采用容错块中的数据对原始矩阵中的故障数据进行替换，达到容错的效果。容错块的计算方式首先通过采用类似卷积神经网络中的池化层处理特征的方式得到每一个块的平均特征，然后利用这些平均特征做数据重构，进而得到容错块。

在卷积神经网络中，池化操作可以降低图像的尺寸，从而减少训练参数，降低计算量，防止过拟合[19]。常用的池化方法包括 mean-pooling、max-pooling 和 stochastic-pooling。其中，meanpooling 使用上一层每个邻域的平均值作为新特征；max-pooling 使用上一层每个邻域的最大值作为新特征；stochastic-pooling 介于两者之间，通过对上一层每个邻域的值按照数值大小赋予概率，再按照概率进行亚采样获得新特征。一般地，mean-pooling 能够限制由于邻域尺寸受限造成估计值方差增大的情况，保留更多的背景信息；而 max-pooling 能够限制由于卷积层参数误差造成估计均值偏移的情况，保留更多的纹理信息[20]。

由于该容错方法使用r×c维的容错块数据，替换X中任意子块对应位置上的故障。所以这些用于替换的数据可能会出现在多个数据块的对应位置。为了使容错后的数据和原始数据间的误差的平方和最小，选择使用类似 mean-pooling求均值的方法得到容错数据。获得容错块Xr的具体步骤如下：

(1)利用分块 PCA 方法对原始数据X进行特征提取，得到降维结果矩阵Y、特征向量矩阵Vk和均值矩阵。

(2)从分块 PCA 的降维过程可知，降维结果矩阵Y、特征向量矩阵Vk和均值矩阵都含有多块数据。在降维结果矩阵Y的每块数据中，将对应位置 32 位数求和取平均，可得到一个Y的均值矩阵，该过程如图 4 所示。按照相同的方式，也对特征向量矩阵Vk和均值矩阵每块数据对应位置数求和取平均，得到相应的均值矩阵和。

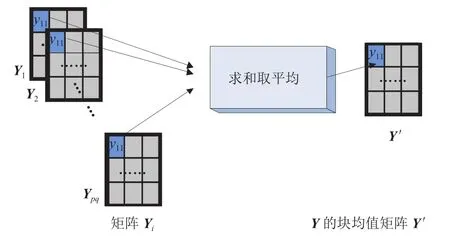
图4 从降维结果矩阵 Y 得到均值矩阵(和同理)Fig. 4 The mean matrixis obtained by the dimensionality reduction result matrix Y(andsimilarly)

3.4 容错替换

当校验位检测到数据X中子块Xwu(0＜w＜p，0＜u＜q)的数据xij(0＜i＜r，0＜j＜c)发生故障时，使用重构的块数据Xr的对应位置数据xij替换该子块中的故障数据xij，然后逐次完成对每个子块中故障数据的容错替换，达到对数据X容错保护的目的。使用Xr对X进行容错保护的流程如图 5 所示。

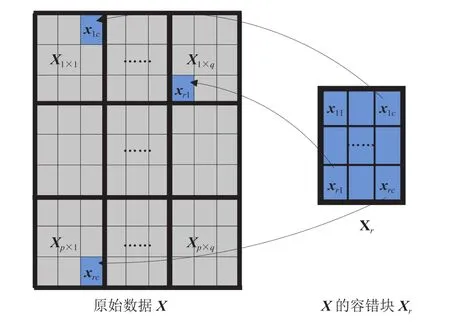
图5 用容错块数据 Xr 替换对应位置的原始数据 X 中的故障数据Fig. 5 The fault data in the original data X of the corresponding position is replaced by the fault-tolerant block data Xr

4 结果分析

4.1 实验建立

采用图片作为实验分析的对象，这样可以更直观地体现出本文容错方法对故障数据的保护效果。通常，峰值信噪比(Peak Signal to Noise Ratio，PSNR)是衡量图像失真或者噪声水平的客观标准，所以本文采用 PSNR[21]来评判经过处理的图片的质量。该值越大，则表明两张图片越相似，一般认为 PSNR 的典型值为 30 dB。

实现图像数据容错保护的具体步骤如下：

(1)对原始数据X中的每一个 32 位数据生成1 位的奇偶校验位；

(2)按照 3.3 节中介绍的获得容错数据的方法，求得容错块Xr；

(3)将Xr、X及X的校验位存入存储器中；

(4)用 rand 函数产生的随机数作为坐标，随机地选中存储器中的数据并进行故障注入；

(5)当需要从存储器中读取数据时，需对数据进行校验位检查。如果检测到故障，用Xr中相应位置的数将故障数据替换；如果没有检测到故障，就可直接读取图片。

本文实验平台基于 Ubuntu 16.04.1 LTS，使用的软件工具有 GCC 5.4.0 和 QMake 2.01a。基于分块 PCA 的容错系统使用 C＋＋实现，其伪代码如算法 1(表 1)所示。

作为对比，下文也使用得到广泛应用的格式为[38,32]的扩展汉明码(纠一检二码)来保护原始数据X。其中，38 位数据为一组，有效数据占32 位，校验位占 6 位。下文的纠错码(ECC)均指纠一检二码。

4.2 实验结果

实验采用 512×512 大小的图片数据为例来展示该容错方法的有效性。图 6 为在不同分割尺寸情况下，各自保留一半主元数目时所对应的执行时间和信噪比统计图。由图 6 可知，将图片切割为 256×8 的子块时，重构效果和执行时间能够得到较好的折中。

表1 基于分块主成分分析的容错方法的伪代码Table 1 The pseudo code based on the fault-tolerant method of modular principal component analysis

图6 执行时间和信噪比统计Fig. 6 The statistics of execution time and peak signal to noise ratio

4.2.1 质量评估

图7 注入不同故障数目时采用容错方法和不采用时的图像结果Fig. 7 Image results of using fault-tolerant and not using fault-tolerant under different numbers of faults injection

由图 7 可以看到，当注入不同数目的故障时，本文提出的容错方法的容错效果明显。如图7(a)、(c)所示，在注入 500 和 1 000 个故障的情况下，由于未受到容错保护，图片质量很差。而当采用本文容错方法之后(图 7(b)、(d))，在注入相同故障数目的情况下，图片质量得到提升，PSNR 值均大于 30 dB。当注入 1 200 个和 1 500个故障时，对比图 7(e)和(f)、(g)和(h)可知，采用本文容错保护方法后，图片保护效果并不是很理想。这是因为此时注入故障数目过多，两个(或偶数个)故障出现在一个数据中的情况逐渐增多，致使检测模块失效所致。

在图 8(a)中，将本文容错方法和 ECC 对图片保护的实验结果做了统计。对于未采用任何保护措施的数据，随着故障数目的增加，图片质量持续下降。对于采用 ECC 保护的数据，在故障数目较少时，图片能够得到较好地保护；在故障数目增多时，图片质量也开始下降。而采用本文的容错方法时，图片质量随着故障数目的增加下降幅度很小。其中，由于 ECC 码会为每个 32 位数据生成 6 位的校验位，所以随着故障数目的增多，故障出现在校验位中的概率也会增加，致使校验位发生比特位翻转的情况增加，有可能将正确的数据改错或导致故障不被纠正，使得图片质量迅速下降。

对于本文容错方法，由于降维数据矩阵Y只保留了原始数据X的主要特征，所以用容错块Xr去替换原始数据中的故障数据。虽然块数据只是原始数据中的近似值，但在故障率为 0.003 5(相当于有 1 000 个数发生故障)时，本文方法仍然能使图片的 PSNR 超过 30 dB。

除了上述单比特故障外，本文还测试了多比特位翻转故障的情况。实验在 0.000 35 错误率的情况下(相当于有 100 个数发生故障)，对这些数据分别注入 0～10 个位翻转的故障，然后统计采用不同保护方式时的图片质量，结果如图 8(b)所示。其中，PSNR 值为 100 时代表图像无损失。当未采用任何保护措施时，随着数据中翻转位数的增加，图片质量迅速下降。若对图片数据采用ECC 保护措施，当只发生 1 位翻转时，能够保持较高的图片质量；而发生多于 1 位翻转时，图片质量迅速变差，这体现了 ECC 方法对于多位故障检测和纠正的局限性。如图 8(b)所示，在发生多个奇数位翻转故障的情况下，经容错后的图片的 PSNR 都大于 30 dB，这体现了本文方法较ECC 方法在多位故障检测和纠正上的优越性。值得一提的是，由于本文对每 32 位数据只生成 1位奇偶校验位，所以只能检测到奇数个位翻转情况，进而当发生偶数个位翻转故障时，图片质量下降。后期可以通过改善故障校验方法来弥补偶数位故障的漏检。

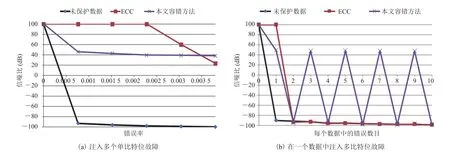
图8 未采用容错保护、采用容错保护和采用 ECC 保护的信噪比结果统计Fig. 8 Statistics on peak signal to noise ratio under no fault-tolerant protection, fault-tolerant protection and error correcting code protection

4.2.2 性能分析

表2 比较了不同图片尺寸情况下，采用不同容错算法的执行时间。从表 2 中可以看出，随着图片尺寸的增加，采用 ECC 的执行时间一直高于本文中的容错方法。这是因为 ECC 是以每个32 位数据为单位进行容错的，而本文提出的容错方法是以数据块为单位对数据作保护的，算法的执行效率较高。

另外，本文也对这两种方法在内存资源消耗方面做了比较，结果如表 3 所示。采用本文的容错方法时，消耗的内存资源明显小于采用 ECC所消耗的内存资源。具体来说，本文所提方法的内存消耗比 ECC 方法减少了约 12%。

综上所述，在数目较少的单比特位翻转情况下，ECC 对数据的保护效果优于本文容错方法，但在对数据精确度要求不高的领域，这是可以忽略的。在纠正多比特位翻转故障、执行时间和内存消耗等方面，本文容错方法均优于 ECC。

表2 本文容错方法和 ECC 的执行时间统计Table 2 The execution time statistics of the fault-tolerant method and error correcting code

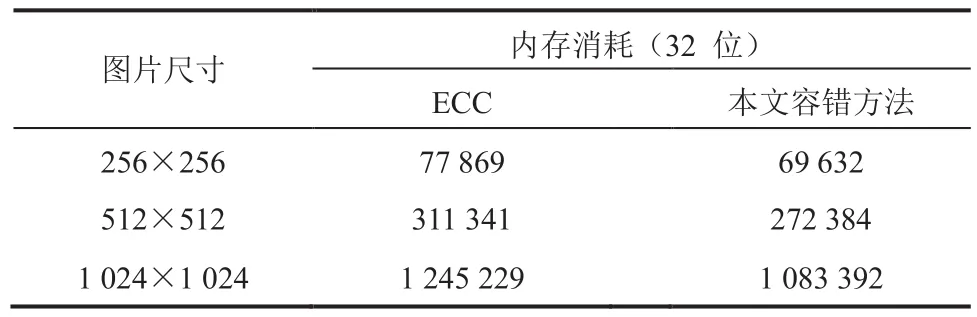
表3 本文容错方法和 ECC 的内存消耗统计Table 3 The memory consumption statistics of the faulttolerant method and error correcting code

5 与国内外相似研究的对比分析

现有级联编码方案虽然可以弥补单一编码方案的缺陷，但增加了计算复杂度，加大了硬件开销。例如，采用基于 RS＋LDPC 码的方案[8]，虽增强了纠错能力，提高了编码效率，但却增加了对于寄存器资源的消耗。

与混合纠错码方式相比，本文所提方法虽然不能精确纠正数据，但在对数据精确度要求不高的领域，如人脸识别等领域，本文方法可以降低计算量，更高效地实现对数据的容错保护，并且不需要消耗寄存器资源，减少了约 6%的硬件资源。

6 结 论

本文提出了一种能够通过容错替换有效保护数据的方法，利用了数据的数学特性，通过特征提取的方式获得该数据的最佳估计，用于替换故障数据。实验结果表明，与基于传统 ECC 容错方法相比，本文提出的容错保护方法可以在不增加硬件开销情况下，获得较好的保护效果，且算法的执行时间和内存消耗都较少。未来拟对故障检测方法及容错保护精度作进一步的研究。