一种有效的图像降噪方法应用研究

聂黎生

（江苏师范大学智慧教育学院，徐州 221116）

0 引言

数字图像作为一种重要的信息形式，通过编码、压缩和传输后会存在不同形式和不同级别的失真，从而降低图像的质量，影响对图像信息的解读。因此在对采集到的图像进行处理前，需要先对图像进行降噪处理。

当前图像降噪方面的研究出现了两大发展主流：基于小波变换理论的图像处理和基于偏微分方程的图像降噪。小波变换作为一种新的多分辨分析方法，可以构造一种既能降低图像噪声，又能保持图像细节信息的方法，解决了传统降噪方法可能破坏图像结构以及边缘细节信息的问题；基于偏微分方程（Partial Dif⁃ferential Equations，PDE）的图像降噪算法，根据图像的特征结构，采取与之相适应的平滑策略，能够保持图像的纹理信息、纹理结构和纹理光滑，取得较为满意的图像降噪效果，在图像去噪、图像增强以及图像分割等领域都得到了很好的应用，成为当前研究的热点[1]。

偏微分方程理论在图像降噪中应用的关键是对偏微分方程的求解，求解方法是一种基于宏观连续模型的自上而下的方法。利用偏微分方程的相关优点，力图解决图像传输过程中的降质问题。通过构建偏微分求解方程，设计出一种适用于图像处理的同步降噪增强算法，实现图像处理中的同步降噪与反差增强功能，从而使图像呈现更加清晰、细腻的视觉效果，达到优化图像的目的。

1 图像降噪

图像降噪与反差增强是图像处理研究的重要内容及改善图像质量的常用手段。图像降噪与反差增强是对立概念，存在一定矛盾性，若先降噪后增强，容易加大图像边缘结构模糊度，并且当降噪不充分时，反而会导致噪声污染更加严重[2]。若先增强后降噪，则容易加大噪声污染程度，对图像质量产生负面效果。

1.1 直方图均衡化方法

直方图均衡化（Histogram Equalization，HE）亦即灰度均衡化，是利用某种灰度映射使输入图像变换为在每一灰度级上都有近似效果的输出图像。在经过均衡化处理后的图像像素占有尽可能多的灰度级并且均匀分布，从而使得图像的立体感、层次性、对比度具有大幅提升[3]。这里利用HE方法，采取以下公式进行求解：

其中，Dy为转换后的灰度值，Dx为转换前的灰度值，H(i)为第i级灰度的像素个数，A0为图像的面积，即像素总数。

1.2 直方图规定化

直方图均衡化通过自动确定灰度转换函数，从而获取具有均匀直方图的输出图像。直方图均衡化对于增强动态范围较小的图像对比和丰富图像的灰度级具有明显的改善效果。但是在某些特定情况下，需要人为控制和设定直方图形状，有选择地增强某个灰度值范围内的对比度或者使图像灰度值满足某种特定条件的分布。

直方图规定化可以用于产生具有特定直方图的图像。在运用均衡化原理的基础上，通过建立原始图像和期望图像之间的某种联系，使原始图像的直方图匹配特定的形状，可以弥补直方图均衡化不具备交互作用的特性。

其匹配原理是首先需要对原始图像作均衡化处理，相应转换和处理公式如下：

同时对待匹配的直方图的图像进行均衡化处理，公式如下：

由于都是均衡化，因此可以令s=v，则有如下关系：

于是，可以按照如下步骤输入图像得到一个具有规定概率密度的图像：

（1）求得变换关系 f(x)。

（2）求得变换关系g(u)。

（3）令 f(x)=g(u)求得变化关系g-1(s)。

（4）对输入图像进行g-1(s)变化，从而出图像。

2 偏微分方程降噪模型

偏微分方程是近年图像降噪方法研究热点之一，其基本思想是根据图像的矢量演化或形变过程进行数学建模，构造一个合适的得到偏分微分方程，然后对微分方程进行求解输出结果图像。偏微分方程的应用是一种基本的迭代格式，通过随时间变化的更新，使得图像逐渐逼近所期望得到的视觉效果。

为了有效抑制图像噪声，同时保护图像边缘结构和纹理信息，达到改善图像质量以便满足更高层次的处理需求，可以考虑在不同区域实现不同程度的扩散。在图像平滑区域，利用较大的扩散速度来尽可能地消除噪声；而图像边缘具有精细结构，往往携带着大部分的纹理信息，这部分应该采用较小的扩散来保留图像的边缘纹理信息。基于P-M方程的图像降噪模型，通过随梯度自适应变化的扩散系数实现去除噪声的同时保护图像边缘特征，进一步提高了图像视觉效果。该方法利用局部特性来控制图像的热扩散方程，提供了一种基于偏微分方程滤波法的新思路。P-M模型可以表示为：

式（5）中，div为散度算子，| ∇u|表示梯度的幅值，g(x)为扩散函数，是梯度幅值| ∇u|的函数，用来规定扩散程度。P-M模型是热扩散的改进，通过扩散函数g(x)来自适应扩散速率，g(x)是梯度幅值| ∇u|的函数，而梯度幅值的大小对应了图像的不同区域，在平滑区域，| ∇u|的幅值较小；在图像边缘细节区域，| ∇u |的幅值较大。由此可知，通过扩散函数g(x)实现了不同区域不同程度的扩散。理论上希望g(x)是单调减函数，提出了两种不同的边缘函数：

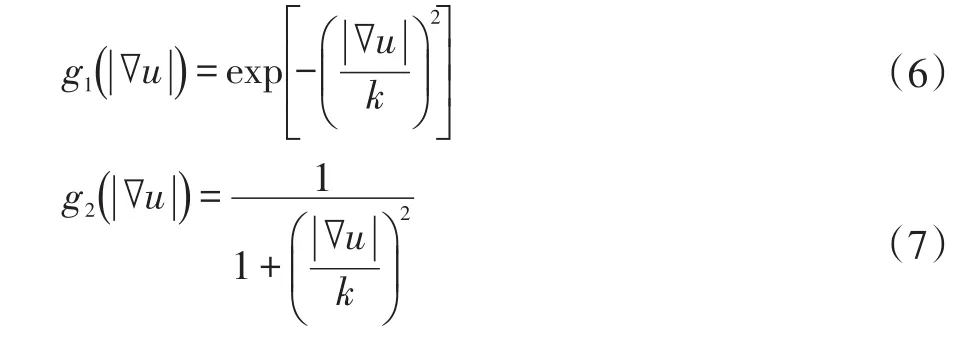
上述表达式中，常数K可以预先设定，在扩散系数函数中作为一个边缘强度阈值，用来调节平滑程度，对图像降噪结果的影响很大。若K的取值过大，扩散过程过度平滑，导致产生的图像信息严重模糊；若K取值太小，则扩散过程过早地停止平滑，导致不能有效去除图像噪声。

P-M模型利用图像的梯度幅值，将图像滤波与图像结构边缘检测进行结合，利用扩散系数来调控扩散量，使扩散主要发生在图像的非边缘区域[4]。P-M模型的局部坐标表达式为：

其中，当扩散函数为（6）时，切线与法线系数gξ和gη分别为：

从式（8）中可以看出，各个方向上的扩散强度随图像梯度幅值| |

∇u的变化而变化，切线方向和法线方向的扩散系数不同，P-M模型将边缘检测和扩散滤波结合起来，实现了自适应滤波。

3 仿真实验

传统算法在图像降噪过程中，图像纹理信息容易受到影响，尤其是纹理的边缘线状结构很容易被破坏。为了说明P-M降噪模型算法的有效性，实验采用分辨率为512×512，每个像素深度为8bit的标准灰度Lena图像，通过MATLAB进行仿真实验研究，如图1（a）至（d）所示。通过偏微分降噪算法与传统算法降噪效果对比，主观上可以看出通过该算法降噪后图像曲率结构保持较好，边缘细节光滑且清晰可见，视觉效果良好。

为了进一步说明算法对抑制噪声的有效性，本文采用两种常用的全参考图像质量评价指标峰值信噪比（PSNR）和图像结构相似度（SSIM）对处理后图像的质量进行客观、定量的评价。表1为本算法与其他算法降噪结果评价指标比较。

实验结果显示，相比基于稀疏表示算法和小波变换算法，其测试的PSNR指标分别提高了5.61%和8.74%；SSIM指标分别提高了7.32%和12.10%，说明本算法从不仅在主观视觉效果上有较好体现，在质量评价标准上也具有优势。

图1

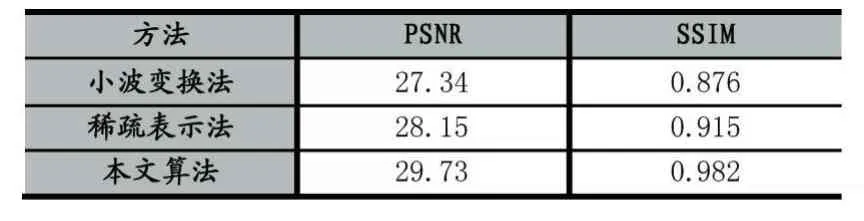
表1 不同算法降噪结果评价指标比较（dB）

4 结语

本文通过仿真实验并通过对实验数据对比分析可知，基于P-M模型偏微分方程降噪方法对图像的边缘部分和内部区域进行了不同程度的扩散，在低噪声密度的图像降噪处理中取得了较好的效果，能够克服传统算法导致的边缘细节信息丢失、边缘模糊及阶梯效应等缺点。接下来还需要对该算法模型作更进一步的研究。