刚性植物对波高衰减和水流结构的影响
2018-11-28刘曙光李小林
陈 明,刘曙光,娄 厦,李小林
(1.同济大学土木工程学院水利工程系,上海 200092; 2.上海市政工程设计研究总院(集团)有限公司,上海 200092)
滨海湿地作为陆地和海洋之间的过渡段,对海岸带环境和生态系统具有重要的影响。湿地植物可以增加水流阻力,削弱波浪冲击,具有固滩护岸的作用;同时能够减轻风暴潮、海啸等极端水文灾害对海岸带的影响;还能够吸收水体中氮、磷等污染物,从而降低进入海洋的污染物浓度,缓解水污染情况。然而因特殊的地理位置和复杂的水动力条件,湿地植物对水动力的影响机理尚未明确,植物分布方式、高度和密度等因素对波浪传播和水流紊动的影响仍需进一步研究。
目前,国内外学者对植物消浪能力开展了大量的研究,对影响波高衰减的关键因子进行了深入分析。Knutson等[1]通过室内试验研究了波浪通过植物区后的波高损失,结果表明波浪在含有互花米草的沼泽地中传播2.5 m后波高衰减了40%,传播距离超过30 m后波高衰减达到94%。杨建民[2]研究发现当植物没有被水流完全淹没时,其被淹没的高度越大,消浪效果越明显,但当波周期与植物摆动周期趋于一致时,植物带基本失去消浪能力。刘达等[3]依据华南沿海的实际情况,模拟了防浪林带不同宽度下的消浪能力,结果表明随着防浪林带宽度的增大,消浪系数在一定范围内线性增大,增大到一定程度后,消浪系数趋于稳定。Luhar等[4]将海草作为研究对象,发现柔性植物对波浪衰减的影响远小于刚性植物;波浪强度越高,海草运动越剧烈;植物与波浪的相对速度越小,波浪的能量损耗越少。Bradley等[5]通过实地监测,发现波浪通过海草植物群时,在前5 m区域内波高增加0.02 m(20%),通过该段区域后波高以指数形式衰减;同时研究发现,海草具有低通滤波器的效果,通过植物区后,波浪频率越高,其能量损耗越多。
植物对波浪的阻碍作用主要体现为植物拖曳力的大小,可通过拖曳力系数CD、植物高度、直径、密度及水流流速来表示,其中CD是一个尤为重要的参数。Dalrymple等[6]利用动量守恒定律,通过研究波与植物的交互作用,提出了关于CD与其他影响因子的波高衰减方程;基于Dalrymple等[6]的结果,Mendez等[7]把研究的波类型由单调的规则波扩展到不规则波,建立了数学模型来分析阻尼系数和CD之间关系,该模型考虑了波浪在不同深度的能量耗散和破碎损失,能够对试验中得到的波高衰减数据进行合理的解释;Sumer等[8-11]也相继开展了CD与水深、波高、波周期、雷诺数Re、KC等参数之间关系的研究。KC是表征阻力大小的重要参数,可以用来描述植物在振荡流场中所受阻力和惯性力之间的相对关系。KC小表示惯性力的影响比阻力的影响要大;反之,紊流阻力的影响比惯性力大。CD与KC关系的研究由Keulegan等[12]开始,他们分析了不同波浪条件下(KC不同)单个植物和植物区分别产生的CD,研究结果表明:在一定范围内,CD随KC的增大而减小,当KC增大到一定程度后,CD趋于恒定值。之后,许多研究都得到了与Keulegan等[12]相同的结论,同时也有研究发现在KC小于10的情况下,CD呈现先增大后减少的规律。目前的研究大多只是对CD与KC的相关性进行定性分析,没有涉及两者在一定变化范围内的具体函数关系。因此,针对CD与KC之间的定量关系,需要开展进一步研究。
波浪通过植物区时,在植物的影响下,水体受到扰动,紊动强度增加,从而影响物质输运和泥沙起动。Pujol等[13-15]对水流在植物群中的紊动能量ETK的规律开展了大量研究,发现波浪通过植物后产生的涡流将水流的平均动能转化为紊动能量,增加了水流的紊动强度,但由于涡流尺度小,冠层内紊动扩散强度较弱。张英豪等[16-17]以含苦草水流的水槽试验数据为基础,选取典型流速剖面,利用象限分析法,研究了苦草对水流结构的影响,发现切应力产生的剪切紊动使得紊动能量在冠顶附近最大,并向冠层内部进行垂向传输;受传输距离的限制,冠层底部水流以每根植物后的涡流紊动为主,紊动能量大幅度减小。目前,对于植物影响下紊动能量分布规律的研究大多针对恒定流及柔性植物,振荡流及刚性植物条件下的紊动能量分布的研究相对较少。因此,本文开展了植物影响下的水动力研究,分析了不同植物密度和淹没类型条件下,波浪通过植物区时紊动能量在纵向和垂向的分布规律。

图1 不同植物区长度的试验布置 (单位:m)
1 试验设计
1.1 试验装置
试验在同济大学水利港口综合实验室的波流水槽中进行,水槽全长50 m,宽0.8 m,高1.2 m。水槽首端设有造波机,造波机的推波板及机械框架安装在距水槽首端约3 m处;水槽末端设有消浪网,用于消除波浪,防止反射波对试验的影响。试验中利用浪高仪(WG)测量波高和波周期,利用三维声学多普勒测速仪(ADV)测量3个不同方向的瞬时流速,两种仪器的布置如图1所示。使用ADV在垂向上分别测量距离底面0.5 m、0.4 m、0.3 m、0.2 m处4个点的流速。为了保证ADV测得数据的有效性,结合Carollo等[18]的研究,本研究将信噪比小于15 dB或相关性小于70%的数据作了删除处理。
1.2 试验方案
试验中选用直径为8 mm的圆柱形木棒模拟刚性植物,将其固定在有机玻璃底板上,放置于水槽中。试验水深为0.8 m,植物区宽度为0.8 m,长度分别为2 m和6 m。选用高度为1.0 m的木棒模拟植物不完全淹没的情况,高度为0.4 m的木棒模拟植物完全淹没的情况。
当模拟低密度分布植物时,木棒横向间距为5 cm,纵向间距为10 cm,植物密度为162.5株/m2;当模拟高密度分布植物时,木棒横向间距及纵向间距均为5 cm,植物密度为325.0株/m2。5组试验植物区布置方案如表1所示,各植物区布置方案下的4组波要素条件如表2所示。
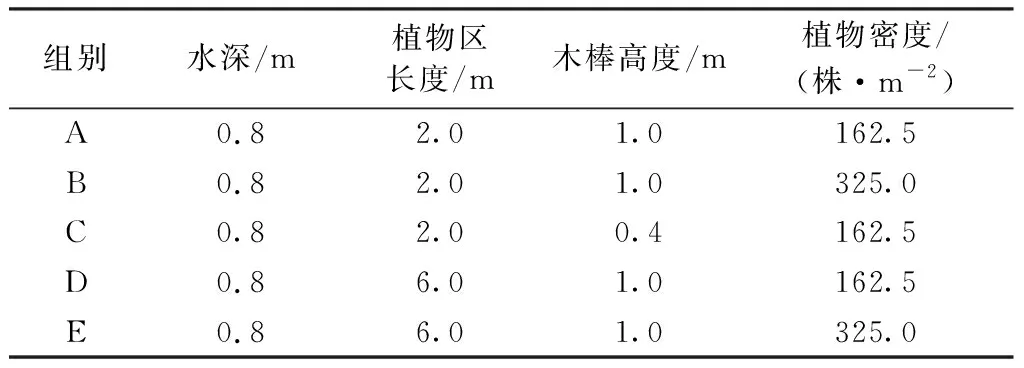
表1 植物区布置方案

表2 波要素条件
2 分析方法
2.1 拖曳力系数CD
Keulegan等[12]提出,水流流经植物群时,在水流运动方向上单位高度植物对水流的拖曳力F可以表示为
(1)
式中:Cm为惯性力系数;ρ为水流密度;A0为木棒截面积;d为木棒的直径;U为水流速度。
由式(1)可以看出,CD是求F的关键参数。根据Dalrymple等[6]的研究成果,结合本文中试验的实际情况进行相应的修改,得到CD的计算公式如下:
(2)
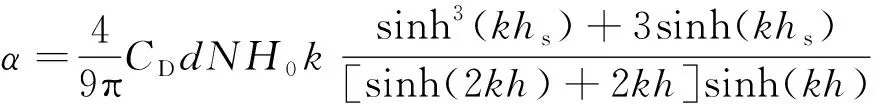
(3)
式中:Kv为相对波高;Hx为距离植物区入口x处的波高,H0为植物区入口处的初始波高;N为木棒种植密度;k为波数;hs为淹没在水中的木棒长度,木棒不完全淹没时其值等于水深h,完全淹没时等于木棒高度hv。
2.2 低科勒冈-卡朋特数KC
Mendez等[7]提出,当植物布置方式比较规则时,CD与KC的相关性比CD与雷诺数Re的相关性更好,因此本文分析了CD与KC的关系。
KC的计算公式如下:
(4)
式中:T为波的周期;Uw为波的最大轨道速度,对于规则波而言:
(5)
式中:a1为振幅;ω为角速度;H为波高。
2.3 紊动能量ETK
波浪传播过程中,植物会对水流结构造成很大影响。规则波的纵向瞬时速度u可以分解为

(6)
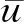
(7)
利用式(6)就可以求出一个波周期内各时刻所对应的纵向脉动流速u′的值。
同理可以求得横向和垂向上的脉动速度v′和w′的值,从而由式(8)可以得到每个测量点处ETK的值:
(8)

3 试验结果与分析
3.1 波高衰减
为了研究植物密度及植物区长度对波高衰减的影响,分析了A、B、D、E这4组植物区布置方案在不同波要素条件下的波高衰减,并利用式(2)(3)计算相对波高Kv和拖曳力系数CD。图2为4组植物区布置方案下不同波在植物区传播时Kv值的沿程变化。
图2(a)为2 m长度的植物区在低密度不完全淹没植物条件下的波高衰减情况。当波浪传播至植物区后端x=2.0 m处,4组波要素条件(工况W1~W4)下的Kv值依次为0.77、0.86、0.89、0.91。随着波高和周期的减小,Kv呈减小的趋势,波浪衰减越剧烈。图2(b)至图2(d)中的波高衰减规律与图2(a)类似,即不同的波在相同布置方式的植物区中传播时,相同位置处短波(工况W1)的Kv值比长波(工况W4)的小,相同的植物条件下短波的波高衰减更多。
在植物区长度相同的情况下,植物密度对波高衰减有很大的影响。在第1组波要素条件(工况W1)下,当植物区长度为2 m时,植物区后端x=2.0 m处,低密度植物影响下的Kv值为0.77(图2(a)),高密度植物影响下的Kv值为0.73(图2(b));当植物区长度为6 m时,植物区后端x=6.0 m处,低密度植物影响下Kv值为0.61(图2(c)),高密度植物影响下Kv值为0.41(图2(d))。高密度植物影响下的Kv值小于低密度植物的Kv值,表明高密度植物具有更强的消波能力。在其他组波要素条件(工况W2~W4)下,植物密度对波高衰减的影响规律与第1组波要素条件(工况W1)下相同。
由图2可以看出,Kv值在植物区前半段减小的程度明显大于后半段,即在各组试验中,随着波在植物区传播距离的增加,Kv值变化的幅度越来越小。由此可以认为,植物对波浪的消减作用在植物区的前段最为显著。

图2 4组植物区布置方案下不同波在植物区传播时的Kv值
3.2 CD与KC的关系
波浪在植物群中传播时,受到植物拖曳力作用,水流结构发生变化,波浪的能量出现了损耗。由式(1)可知植物拖曳力系数是描述拖曳力大小的重要参数,对分析流速变化和波能衰减具有重要意义。
图3为A、B、D、E这4组植物区布置方案下的CD-KC关系曲线,这4组方案中KC的变化范围为4.5~23.0,CD值的变化范围为2.2~5.3。由图3可见,4组曲线的CD都随着KC增大而单调递减,但是减小的速率逐渐变缓,当KC达到20左右时,CD稳定在某一常数附近。该现象与Keulegan等[12]得出的CD随着KC的增大先减小后趋于稳定的研究结论是一致的。
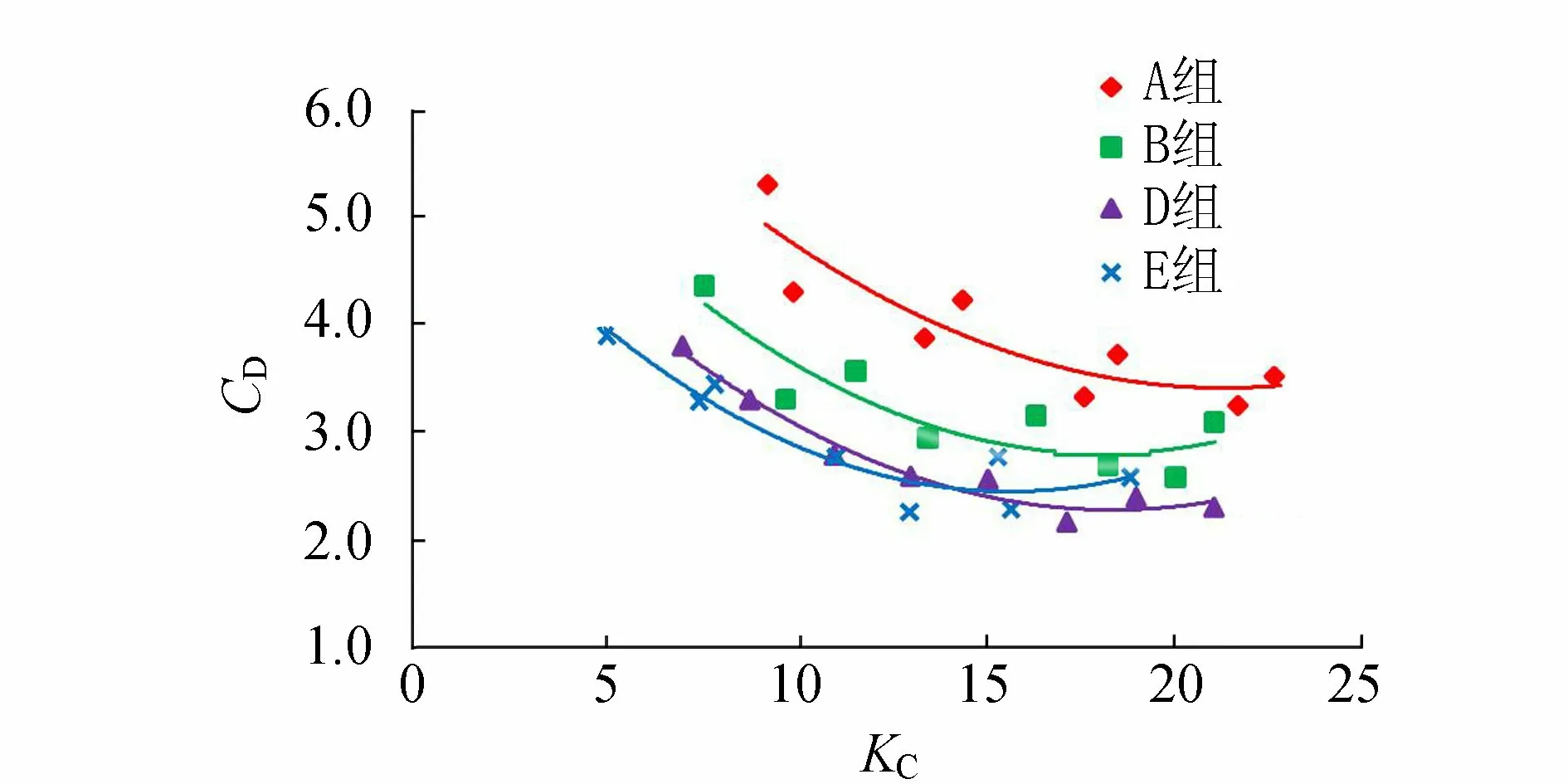
图3 4组植物区布置方案下的CD-KC曲线
对4组试验结果进行回归分析,发现CD和KC之间符合二次函数关系,如式(9)所示,且相关系数的平方值R2均不小于0.79,各项系数见表3。
(9)

表3 4组植物区布置方案下的CD-KC曲线拟合函数的系数
在KC的取值范围为4.5~23.0,不完全淹没植物的密度为162.5株/m2及325.0株/m2的条件下,各组拟合方程的二次项系数均在0.012左右,一次项系数均接近-0.423,仅常数项差别相对较大。由此可见,在不同植物区布置方案下,CD-KC关系曲线变化趋势类似,植物特征主要反映在CD-KC关系曲线的常数项上。在本试验的植物区布置方案和波要素条件下,植物区内部的CD-KC关系可通过取4组拟合方程中系数的平均值来进行快速估算,如式(10)所示。表3中4组方案的二次项系数、一次项系数和常数项系数与式(10)的误差范围分别在16.7%、5.4%、21.2%之内。同时,在表3中可以看到4组实测数据与式(10)的均方根误差ERMS≤0.85,所以用式(10)来拟合4组的CD-KC关系是可行的。
(10)
植物区长度为2 m时,A和B组的CD在2.6~5.3的区间内变化;植物区长度为6 m时,D和E组的CD在2.2~3.9的区间内变化。当KC相同时,A和B组的CD值均比D和E组的大。A、B组拟合曲线的R2值分别为0.80、0.79,D、E组拟合曲线的R2值分别为0.97、0.89,表明D、E组CD和KC的相关性更高。由于水流的发育程度不同,植物区长度对CD存在一定影响,从而影响了CD和KC的相关性。
3.3 紊动能量ETK
为了检验流速数据的准确性,对每组数据进行能量谱密度分析,图4是工况W4下x=3.0 m,y=0.3 m处的数据分析结果。由图可以看出,在0.85 Hz左右存在一个很明显的波峰,而工况W4的波周期是1.2 s(频率为0.83 Hz),2个频率值是相近似的。在5~100 Hz范围内(非波峰段),可以用一段直线模拟紊流速度谱密度的斜率变化,该段直线的斜率为-5/3,即波浪流速的波谱特征满足能谱的-5/3次方定律。所以,图4的能量谱密度分析可以证明所测流速数据的可靠性。

图4 工况W4下x=3.0 m,y=0.3 m处的速度能量谱密度
图5为A、B、C、D这4组植物区布置方案及第2、3组波要素条件(工况W2、W3)下ETK在垂向的变化,其中纵坐标z代表测点距离底面的高度,ADV测点位置如图1所示。
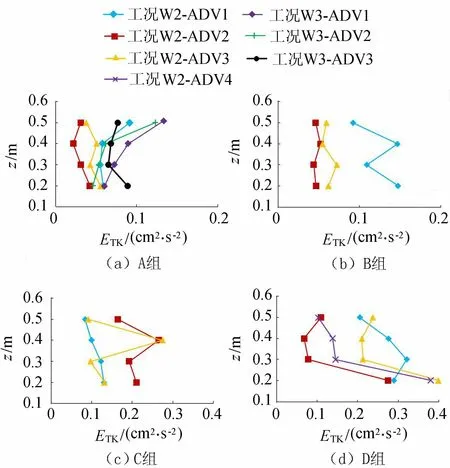
图5 4组植物区布置方案及工况W2、W3下ETK的垂向分布
在图5(a)中,ADV2测量得到当z从0.5 m变化至0.2 m时,第2组波(工况W2)的ETK依次为0.03 cm2/s2、0.02 cm2/s2、0.03 cm2/s2、0.04 cm2/s2,而第3组波(工况W3)的ETK依次为0.12 cm2/s2、0.06 cm2/s2、0.05 cm2/s2、0.05 cm2/s2。由此可以看出,在各个垂向测点上,工况W3的ETK均比工况W2的大,即波高越大,相同植物区布置条件下各位置处的ETK越大。
对比图5(a)和图5(b),波要素相同的条件(工况W2)下,植物密度对ETK有一定影响。低密度植物条件下(图5(a)),ADV2和ADV3测量得到植物区内ETK的变化范围是0.02~0.05 cm2/s2;高密度条件下(图5(b)),ETK的变化范围是0.04~0.07 cm2/s2。由此可见,ETK随着植物密度的增大而增大。这是因为植物密度越大,引起的单根植物尺度上的紊动越剧烈,从而导致ETK越大。
图5(a)和图5(c)分别为工况W2下,不完全淹没植物和完全淹没植物影响下的ETK分布。植物不完全淹没时(图5(a))的ETK(0.02~ 0.09 cm2/s2)明显小于完全淹没时(图5(c))的ETK(0.11~ 0.35 cm2/s2)。由图5(c)可见,在完全淹没植物的影响下,ETK最大值出现在z=0.4 m处,即植物顶端。当植物完全淹没时,在植物顶端附近存在一个剪切层,其剪切力会导致水流在该处产生流速差,从而紊动情况有明显的增强。这一点与张英豪等[17]通过研究柔性植物在水流条件下得到的结论一致。
由图5(a)、图5(b)、图5(d)可以看出,当植物不完全淹没(植物高度为1.0 m)时,在植物区入口前方0.25 m处(ADV1)的ETK比植物区内部的大,即植物区对前方0.25 m处(x=-0.25 m)区域的水流紊动情况有很大影响。可以将植物区前方一段区域视为紊流增强区,波浪在即将进入植物区时,由于突然受到植物的阻力影响,流速降低,形成一个流速梯度,紊流情况得到加强,表现为该段区域ETK增加。
在图5(d)中,z=0.3 m处,ADV2、ADV3、ADV4测量得到的ETK分别为0.08 cm2/s2、0.21 cm2/s2、0.15 cm2/s2;z=0.2 m处, ADV2、ADV3、ADV4测量得到的ETK分别为0.27 cm2/s2、0.40 cm2/s2、0.38 cm2/s2。当植物区长度为6.0 m时,在接近水槽底部一定距离时植物区内的ETK会出现增大的现象。水流流过植物区时,会在每根植物后形成涡流,而这部分涡流主要集中在植物根部,导致相应的ETK较大。但在图5(a)至图5(c)中,这种现象并不明显。这与3.2小节中得出的结论一致,即植物区长度不同所造成的水流发育程度的差异对ETK的分布规律具有一定影响。
4 结 论
a. 对于规则波而言,波高和周期越小,通过植物区时波高衰减越快。植物密度及植物区长度越大,波高衰减越多。波浪在植物区传播时,波高衰减主要在植物区前段,之后衰减速度越来越慢,所以增加植物区长度有助于植物对波高的消减,但其消波效果随着植物区长度的增大而逐渐减弱。
b. 当KC在4.5~23.0之间变化时,植物区内拖曳力系数CD随着KC的增大而不断减小,但是减小的速率逐渐变缓。对于不完全淹没植物,两者之间的关系可以用二次函数CD=0.012KC2-0.423KC+c进行拟合,其中常数项c的值由植物区布置方式决定。
c. 波高、植物密度的增大均会导致植物区内部ETK的增大。和不完全淹没相比,植物在完全淹没时ETK更大,且从水面至底面ETK呈先增大后减小的规律,并在植物冠层处达到最大值。植物区前方一段距离内存在一个紊流增强区,该区域内的ETK明显增大。植物区长度为6 m时,在接近植物根部会出现ETK增大的现象。植物区长度不同所造成的水流发育程度的差异对ETK的分布规律具有一定影响。
