基于GRA-LSSVM密度法的配电网空间负荷预测方法研究
2018-11-28,
,
(1.辽宁省数控机床信息物理融合与智能制造重点实验室, 辽宁 抚顺 113122;2.沈阳工学院 机械与运载学院,辽宁 抚顺 113122; 3.沈阳音乐学院 艺术管理系,沈阳 110168)
0 引言
配电网是电力系统的重要组成部分,在电力系统中起着连接电力用户和发电厂的作用,配电网的结构对其电力系统的供电质量和效率有很大的影响,因而配电网设计是一项重要的工作。配电网的结构主要包括电网设备的容量、分布位置和联接方式,其涉及到的参数很多,因而相应的设计难度很大。目前我国的配电网的网络建设水平和社会的电力需求方面还存在一定的差距[1]。对一些供电很复杂的城市配电网经常出现,供电瓶颈,电网设备过负荷相关的问题[2]。这些都从一定程度上说明了配电网和实际的电力需求之间还存在一定的差距,从而对生产和生活带来一定的影响。因而很有必要提高配电网规划水平,对其进行合理的规划和改造、以此来有效的提高供电质量和效益、为满足电力需求起到帮助作用。
在进行配电网设计时首先需要做好电力需求预测工作,这是确定电力系统发展规划基本条件,此种预测结果和电力系统规划和设计有密切的关系,可也为电力系统的安全、可靠、提供良好的支持,且对电力市场交易也可以起到一定的参考作用,因而准确的预测出电力需求结果有多方面的作用[3]。
此种电力需求预测可以具体划分为总量负荷预测(GLF)和空间负荷预测(SLF)两种类型的,前一种主要是预测出一个区域的电量,在预测时主要是参考相应的历史电量、负荷等数据,并通过相关预测函数确定出未来一定时间目标区域内的总电量。这种预测属于战略层次的,所得的结果可也为发电计划的制定起到一定的参考作用。而后一种预测方法主要是通过空间负荷预测的,在预测时先将规划区域细分为各小区,然后具体预测出各小区未来的电量值,并求和而得到空间电量。此种预测所得结果可也为相应的变电站的容量、型号、开关设备等参数的确定提供参考[4]。
薛远天等围绕着如何减小电网负荷规划中预测误差过大问题,提出以加强系统稳定安全运行为前提,讨论了电网的安全结构问题[5]。刘思等针对电网负荷密度的地区差异性,提出了一种电网负荷的分类校验和精选方法,该方法是基于电网的日负荷曲线[6]。刘思针对电网负荷预测问题,结合目前应用较广的数据挖掘技术中的聚类技术,实现对电力系统中日负荷曲线的精确分析,并基于此提出了日负荷曲线聚类算法,该算法是基于负荷特性指标降维实现的[7]。彭玉芹为实现电网负荷的精确预测,采用的方式是将用电总量负荷预测和地域空间负荷预测相结合的方式。并采用人工神经网络的方法进行总量负荷预测,目的是消除负荷预测的不确定性[8]。黄强认为只有对需要的配电的各个区域的负荷非常明确的情况下,才能够实现对配电网的合理规划,进而确定变电站的位置、对应的体积和线路的走向[9]。黄晓晖围绕着电网空间负荷预测的方法进行了分析,阐述了预测的种类和流程,同时结合相关实例阐明了应用效果[10]。
本文针对配电网空间负荷预测,设计了一种新型的电网负荷密度预测算法,在算法中将支持向量机引入到基于灰色关联度分析的负荷预测模型。通过实际数据对这种算法的性能进行实例分析,依据分析结果表明,本文提出的算法与不采用本文方法对配电网空间负荷预测的精度有显著差异,本文方法可以有效的提高配电网负荷密度预测的精度。
1 负荷预测种类及相关因素分析
现有的电力负荷预测方法数量非常多,如果按照负荷预测的一般原理进行分类,主要分为用地仿真类的空间负荷预测方法、基于密度指标的负荷预测方法、基于趋势类的空间负荷预测方法、基于多元变量法的负荷预测方法。另外,还可以根据负荷预测过程能否写出解析表达式进行分类,主要分为解析类用电负荷预测方法和非解析类用电负荷预测方法;第三种方式是从确定元胞负荷与总量负荷的先后顺序进行的,主要分为两类:一种是自上而下的负荷预测方法,另一种是自下而上的负荷预测方法。具体分类情况如下:
1)根据负荷总量进行预测,也就是依据目标区域内相关的历史分类负荷来预测出未来一定时间的分类负荷。
2)在历史分类负荷基础上利用相关方法推算出各类负荷的相关性,然后通过总负荷按比例进行划分。也可以根据目标区域的实际情况来确定出分类负荷所占的比例。也可以在比例基础上根据总电量来预测出分类用电量,再通过这种比例方法进行分配时,应该确保各类负荷同时率,这样所得结果才是可行的[11]。
3)用地仿真类的空间负荷预测方法。该种方法主要有以下8种方法:基于模糊逻辑控制技术的用地仿真法、基于粗糙集理论的用地仿真法、基于元胞自动机的用地仿真法、基于蚁群算法的用地仿真法、基于负荷细分与SVM技术的用地仿真法、基于系统动力学与运输模型的用地仿真法、非均匀区域用地仿真法、考虑不确定性因素的用地仿真法。
4)负荷密度指标法。该种方法主要有传统、智能算法和发展曲线等三大类方法。传统方法又可分为直观预测法也称之为涂色法和分类负荷平均密度指标法等两种方法。智能算法可划分为:基于双层贝叶斯模型的负荷密度指标法、基于模糊理论的负荷密度指标法、基于AHP和TOPSIS的负荷密度指标法、基于ANFIS的负荷密度指标法和基于LS-S VM的负荷密度指标法。发展曲线预测方法主要有:基于VAI的负荷密度指标法、基于饱和密度与相对系数的负荷密度指标法和计及元胞属性及发展时序的负荷密度指标法。
5)用电负荷的多元变量预测法,主要是基于经济计量模型的负荷指标预测方法。
6)趋势类预测法。该种方法主要以下几种方法:元胞负荷转移招合法、负荷规律性分析法、空区推论法(或模板法)、元胞负荷聚类分析法。负荷预测的外推算法主要有:回归分析法、指数平滑法、增长速度法、生长曲线法、灰色理论法、马尔可夫法、灰色马尔可夫法等7种。
在进行配电网规划时,还应该确定出目标区域的分类负荷,可以根据此结果为各类小区的负荷总量控制提供依据,在修正总量负荷预测时也用到此结果。总量和分类负荷存在密切的关系,二者之间可以进行相互校核,这样可以使得预测结果的精度更高。二者的关系具体如图1所示。
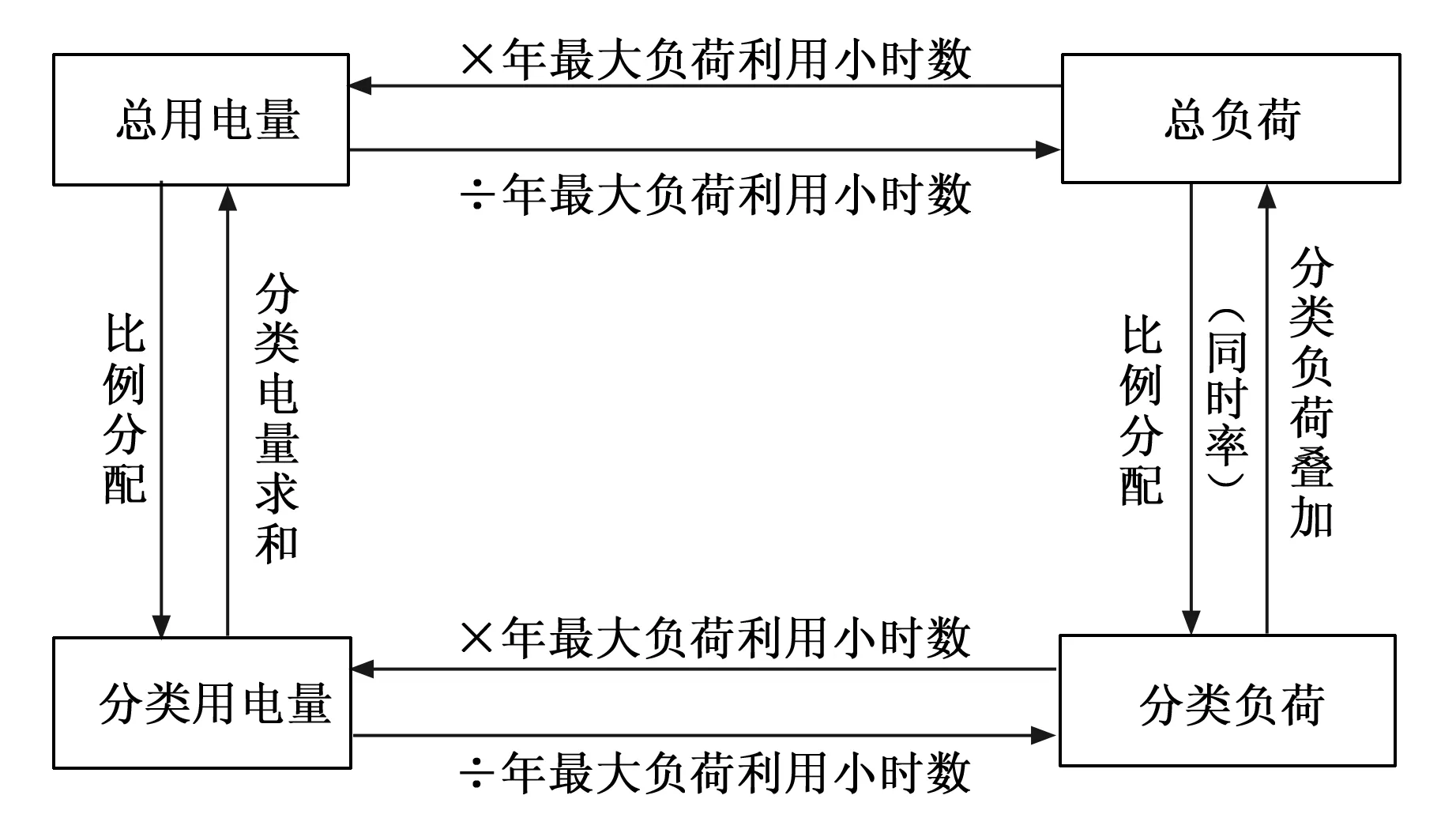
图1 总量负荷与分类负荷内在联系图
总用电量通过各个小区用电量的比例分配可以得到每个小区的分类用电量,每个小区分类用电量的和就是总用电量。总用电量和总负荷之间的关系是:总用电量/年最大负荷利用小时数就是总负荷,总负荷乘以年最大负荷利用小时数就是总用电量。分类负荷和总负荷之间的关系为:总负荷按照各个小区的分配比例进行分配,得到分类负荷,分类负荷叠加得到总负荷。总用电量和分类负荷之间,总负荷和分类用电量之间没有直接的关系。
可以对比分析以上方法所得的分类负荷预测值,在所得结果基础上再通过专家干预来得到最终的目标值。
2 基于 GRA-LSSVM 负荷密度法的空间负荷预测
2.1 基本原理
在进行电量预测时,也可以以用到支持向量机工具,其属于一个三层结构的学习机器,其总体架构情况见图2。
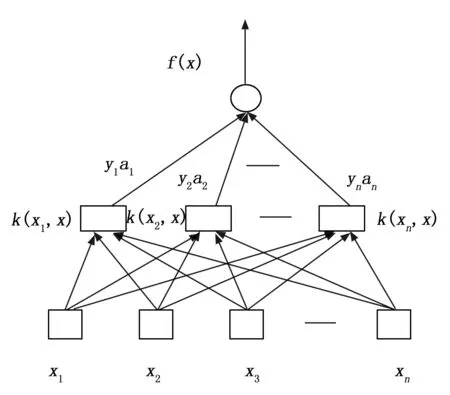
图2 支持向量机的体系结构
此架构中最底层的x1,x2,x3,...,xn是输入样本,K(xi,x)(i=1,2,...,n)是样本x与支持向量的内积,αi(i=1,2,...,n)是拉格朗日乘子。通过支持向量机进行分析时,先依据其相应的逻辑概念框架,确定出对应的输入,之后在此基础上确地出合适的核函数,之间输入样本,并在优化基础上确定出相应的决策函数,通过这种方法求解和传统的神经网络有一定的区别和联系,二者的区别表现为:神经网络结构有很多是根据经验选取的,不能很好的得到相应泛化的置信空间界限,因而其推广性能较差,且在求解过程中可能出现过学习的现象。而支持向量机在进行求解时主要用到了最小化归纳原理,并通过这种原理来控制学习单元的VC维的边界,这样可以使学习单元控制在一定的范围内,就不会出现过学习的缺陷[12]。
最优分类面可以将两类很好的区分开,且可以确保分类间隔最大。如果利用风险最小化原则进行分析,也就是通过一定的分类使得VC维最小,等价于使界中的置信范围最小,以便得到最小的风险结果,且VC维最小。
假定给出一个样本集(xi,yi),i=1,...n,x∈Rd,y∈{+1,-1},满足:
yi[(ωtxi)+b]-1≥0,i=1,...,n
(1)
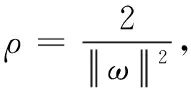
(2)
s.t.yi[(ωtxi)+b]-1≥0,i=1,...,n
(3)
为了确定出式(2)的最小值,可以通过如下拉格朗日函数求解:
(4)
其中:αi≥0为各样本相关的拉格朗日乘子。为得到式(4)的极值,可以通过此泛函对ω、b求偏导,这样就可以确定出式(4)相关的对偶函数:
(5)
(6)
根据式(6)的相关的约束,确定出式(6)的唯一解αi,这样不等于零的拉格朗日乘子αi相关的样本为支持向量。

(7)
(8)
其中:x*(1)、x*(-1)分别表示两类中之一的支持向量。
通过以上方法确定出的参数ω、b可确定出相应的决策函数:
(9)
2.2 算法设计
2.2.1 建立负荷密度指标体系
在进行算法设计时,建立负荷密度指标体系可以得到不同类型负荷的影响因素和这些因素相应的样本库,这样可以为预测小区电量提供参考和依据。这种指标体系可也为预测模型提供相应的训练样本集,为得到更精确的预测结果提供支持,相应的建立过程具体如下:
1) 结合城市规划,确定出不同负荷的分类:如果规划区已经设计出相应的城市规划图,则区域内的负荷可以总体上划分为 10 类,也就是商业负荷、居民负荷、设施负荷、市政设施负荷、绿化和照明负荷[13]。
2) 确定出影响这些负荷密度值相关因素,这可以通过电力系统的抄表系统和建筑规划部门的数据库得到。统计分析出不同类型负荷密度相关的影响因素,对这些因素值的数据资料保存处理。
3) 确定出负荷密度相关的指标体系:得到不同类型负荷的样本数据,确定出负荷相应的密度值和与之对应的样本数据库。这样可以帮助进行电量预测。
通过以上方法就可以确定出相应的负荷密度指标体系,具体情况见图3。
通过这种体系可以为相应的预测模型提供支持,从而有效的提高预测精度;也可以为模型修整提供支持和帮助。
2.2.2 选择 LSSVM 预测模型的训练样本
确定出相应的待预测小区的影响因素,然后将这些因素的属性值当做预测样本,确定出此体系中目标区域内预测样本和因素样本的灰色关联度,并依据此所得界确定出训练样本,本文在研究时选择了分辨系数ρ=0.5 条件下,二者的灰色关联度大于 0.95的样本作为与此相应的训练样本。
2.2.3 预测待预测小区的负荷密度值
本文对小区的负荷密度通过这种优化后的LSSVM 模型来预测,相应的预测步骤如下:
1)数据预处理:也就是归一化处理相应的原数据样本,然后将相应的影响因素属性值当作为此模型的输入,输出结果为负荷密度值,这样能就可以得到如下的公式:
(10)
其中:xmax表示不同各影响因素属性值对应的最大值。
2)选取核函数:确定出相应的径向基函数,然后将其当过此模型对应的核函数。
3)通过 PSO 算法对此模型参数进行优化。
4)将优化所得的参数C和σ 输入此种模型中进行预测分析 ,这样就可以得到相应的密度预测值。
小区未来负荷Wi可以通过负荷密度值和小区的面积乘积来表示,具体表达如下:
Wi=yi*si
(11)
基于 GRA-LSSVM 方法进行预测的流程具体如下:
具体见图 4 所示。
3 仿真实验
接下来主要是以实际的居民小区为例进行负荷密度值的预测,并对本文提出模型的有效性进行验证,在验证前先收集此小区电力负荷和相应的样本数据,具体结果见表1。在此表中:A1为人口密度;A2为人均收入;D 为负荷密度值,相应的样本数据如下。
通过数学实验软件平台确定出相应的预测模型,此模型的参数具体为:粒子群规模为 40,混沌最大迭代步数为20,学习因子c1和c2都是2。通过优化之后得到C=23.475。
而根据实际结果表明,本小区实际负荷密度值为 7.54千瓦每平方千米,本文通过这种模型预测所得结果为8.10千瓦每平方千米,误差只有0.019 5。如果样本没有通过灰色关联度训练,则相应的预测值为 8.70 千瓦每平方千米,相对误差达到了很高水平,而在没有利用混沌 PSO 优化算法情况下,所得预测值为 8.20 千瓦每平方千米,对应的误差为 0.036 5。据此可以看出将这两种算法引入进行预测,可以显著的提高预测准确度。

图4 空间负荷预测总流程示意图

序号A1/(人/km2)A2/元A3/(kwh)A4/%D/(kw/km2)13065113511.011.0622161504838.010331627.032930911221.010.034257011000.083431320.05173032881.063660511.06166001222.010192632.07158552609.06286929.08319501269.054277211.09176534919.099411722.0………………120258531013.081527221.0
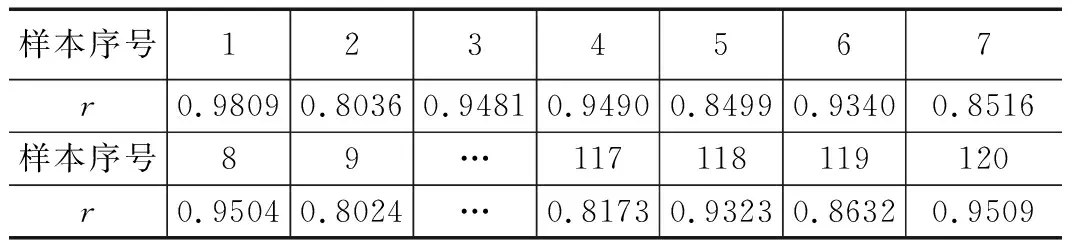
表2 预测小区样本与各参考样本的灰色关联度r

表3 三种不同方法预测结果比对
4 结论
本文主要是设计了一种新型的电网负荷密度预测模型,在研究时将灰色关联度引入到基相应的配电网空间负荷预测中,这样可以更好的预测出负荷密度值。随后本文对这种算法的性能进行了实例分析,根据所得结果表明,这种方法和不引入两种算法的预测精度有显著差异,可以有效的提高负荷密度预测的精度。
