电传飞机飞行品质低阶等效系统算法研究
2018-11-28,,
,,
(中国飞行试验研究院 飞机所,西安 710089)
0 引言
电传操纵系统现在已广泛应用于新型军民用飞机,极大地改变了飞机动力学系统的特性。电传飞机飞行品质的评价和验证面临着新的技术挑战。
飞行品质规范[1]普遍建议使用低阶等效系统的方法评定电传飞机的飞行品质。用具有固定形式的低阶等效系统代替高阶系统,使用优化方法给出低阶等效系统的参数,计算飞行品质指标,评定飞行品质等级。[2-3]采用低阶等效系统的方法评定电传飞机飞行品质必须确定电传飞机的低阶等效系统模型,然后寻找合理的寻优算法,保证低阶等效系统能够合理有效地反应电传飞机动力学系统的特性。
对于早期没有电传操纵系统的飞机,由于飞机动力学系统的输入即为飞行员的操纵,飞机舵面与飞行员操纵基本呈线性关系,从飞行动力学方程简化得到的小扰动方程即可反应飞机动力学系统的模型。小扰动方程为典型的线性系统,模型结构简单,没有时间延迟,辨识方法较为成熟,国内已经传统机械操纵飞机的飞行品质评定中总结出了有效的辨识算法。但是,电传操纵系统的使用使得飞行员的操纵输入与飞机舵面不再是简单的线性关系。电传操纵系统的引入使得飞机动力学系统不再是简单的线性系统,反馈控制、滤波器等控制环节的引入极大地增加了飞机动力学系统的阶次,时间延迟的引入也增加了系统的非线性。传统的辨识算法已不能够满足电传飞机飞行品质评定的需求,存在时间延迟干扰大、参数初值敏感性高、辨识结果可靠性低等问题。
本文在飞机小扰动方程线性系统模型的基础上,添加时间延迟项,建立以气动导数和时间常数为待辨识参数的飞机动力学系统传递函数模型,以某型电传飞机飞行试验数据为模型输入和输出,对高阶系统进行频域分析,综合运用方程误差法、输出误差法和单纯形法等多种频域寻优算法,辨识飞机的低阶等效系统模型参数,计算电传飞机飞行品质指标,评定飞行品质等级,为飞行品质评定提供技术支持。
1 低阶等效系统模型
电传飞机纵向动态特性包括长周期和短周期模态,横航向动态特性包括荷兰滚、滚转和螺旋3种模态。其中纵向长周期模态和横航向螺旋模态均为弱模态,本文主要研究纵向短周期和横航向荷兰滚、滚转等复杂模态。
根据小扰动理论,飞机的纵向短周期模态可以用式(1)表示[6][12],其中,ɑ为迎角,q为俯仰角速率,Nz为法向过载,δe为飞机的纵向杆位移。由于迎角的测量误差较大,在飞机的纵向短周期模型中,将迎角作为系统的状态量,将俯仰角速率和法向过载作为系统的输出量,纵向杆位移为系统的输入量。将式(1)所示的状态空间模型进行拉普拉斯变换,可以获得飞机纵向短周期模态的传递函数模型,以[a0,a1,b0,b1,c0,c1]代替复杂的拉普拉斯变量系数,增加时间延迟项,可以得到如式(2)所示的纵向短周期模态传递函数模型。
(1)
(2)
同理,飞机的横航向小扰动方程可以用式(3)表示[2-3],其中β为侧滑角,p为滚转角速率,r为偏航角速率,Ny为侧向过载,δa和δr分别为横向杆位移和脚蹬位移。对式(3)进行相似的处理,以滚转角速率和偏航角速率为系统输出,可以得到如式(4)和(5)的荷兰滚、滚转模态的传递函数模型。
(3)
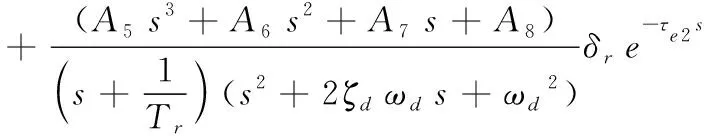
(4)

(5)
基于以上传递函数模型计算其特征根,从而得到飞机的纵向短周期无阻尼自然频率、阻尼比,荷兰滚无阻尼自然频率、阻尼比,滚转模态时间常数等飞行品质指标。用特征根计算飞行品质指标的计算方法详见参考文献6,本文不再赘述。
2 频域相干性分析
频域参数辨识方法需要对系统的输入输出进行频谱分析,而相关函数则是一种重要的检查输入输出因果关系的方法。相干性分析可以为频域参数辨识方法确定辨识的频率范围。对于已知的系统输入和系统输出,根据快速傅立叶变换(FFT)方法,可以得到输入输出的频谱[4]:
X(f)=FFT(x),Y(f)=FFT(y)
(6)
自相关函数定义如下:
(7)
其中:T表示记录的时间段长度,互相关函数定义如下:
(8)
根据以上公式,可以得到各个频率点的相干系数定义如下:
(9)
相干系数分析可以确定辨识的频谱信息范围,以下列输入输出信息为例,如图1~2所示。
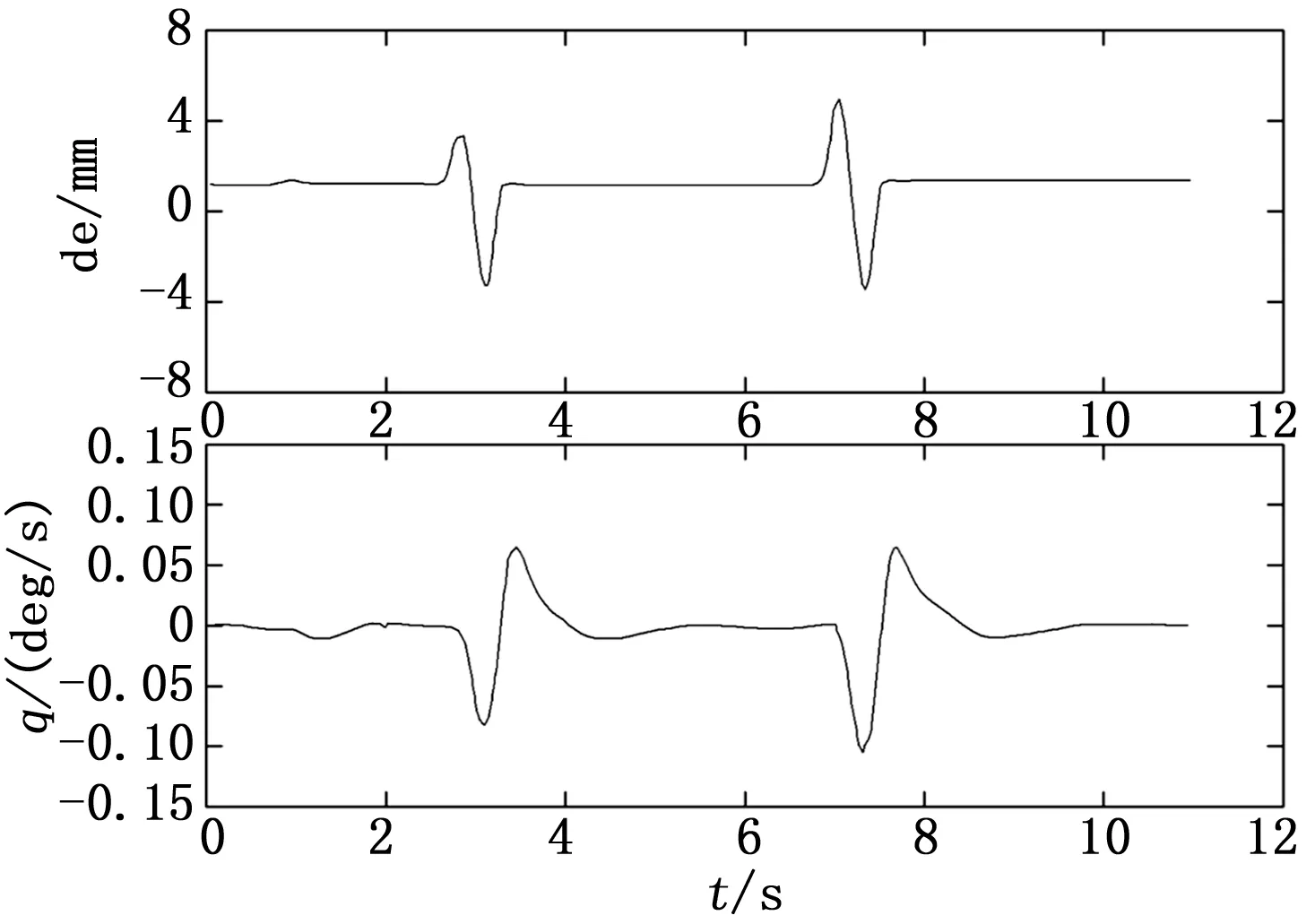
图1 输入输出时间历程

图2 相关系数
根据图1和图2所示,在2~15 rad/s的频率范围内,输入输出的相关度较高,而飞行品质关心的频率范围为0.1~10 rad/s,因此确定频域参数辨识的频率范围为2~10 rad/s。
3 高精度有限傅立叶变换
高精度有限傅立叶变换[5]可以对有限长度的时域信号在指定的频率范围内进行分解[2]。结合本文第二节的相关性分析结果,可以得到指定频率范围内的精确的频谱信息。
假设所选择的频率范围为f∈[f0,f1),并且取定M个离散频率点
fk=f0+kΔf,k=0,1,2,…,M-1
(10)
其中:f=(f1-f0)/M。因此离散傅立叶变换可以写为如下形式:
k=0,1,2,…,M-1
(11)
定义
Φ0=2πf0Δt,ΔΦ=2πΔfΔt
A=ejΦ0,Z=ejΔΦ
代入上式可以得到:
(12)
随着k的增加,AZk表示在Z平面上单位矢量画出的轮廓线。Ф0表示单位矢量的初始位置的角度和位置,和初始频率f0有关;△ Ф表示沿着单位圆随着频率的增加而导致的角度和位置增量,和△f与k有关。对以上形式使用参考文献[2]中的修正方法,即可得到准确的高精度有限傅立叶变换。
4 参数辨识算法
本文使用频域方法计算低阶等效系统的参数值。根据试验数据的高精度有限傅立叶变换得到的频谱信息,利用频域方程误差法和单纯形法可以得到合理的待辨识参数的近似值,进一步使用输出误差法进行迭代,可以得到最终的参数值。
根据时域极大似然法原理[6],对于飞行器动力学系统而言,极大似然函数形式:
(13)
其中:R为加权矩阵,无特殊要求时,无差别的定义R为单位阵。根据傅立叶变换的帕斯瓦尔定理,以纵向短周期模型为例,可以定义频域极大似然函数如下:
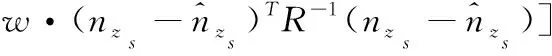
(14)
其中:w为加权系数,用以平衡似然函数中俯仰角速率与法向过载之间的权重。一般情况下,我们定义加权系数如式(14)所示。加权系数可以根据拟配计算的实际情况进行调整以获取更好的拟配效果。
(15)
4.1 方程误差法
频域方程误差法计算方法简单,可以为输出误差法提供迭代待初始值。以纵向单拟配为例,将式(2)纵向短周期传递函数模型中的拉普拉斯变量s替换为jω,改写为:
(16)
(17)

(18)
代价函数为:
(19)

⟹θ=(XXT)-1XTY
(20)
方程误差法需要给出时间延迟的初始值。实际计算中,可以取输入数据和输出数据第一个峰值之间的时间差作为时间延迟的初值。方程误差法可以通过简单的一步迭代获取待辨识参数的初步估计值,提高后续迭代计算的效率。
4.2 单纯形法
单纯形法在多参数优化函数最值问题中有广泛的应用。单纯形法的计算原理在参考文献[4]中有非常详细的介绍。单纯形法的优点是对于初值的选取不敏感,且迭代收敛特性好;缺点是迭代收敛速度比较慢,计算量大,对于未知参数较多的情况,单纯形法往往不能得到合理的解。综合使用单纯形法和方程误差法,可以为输出误差法提供非常接近最优解的初值,为保证输出误差法的迭代收敛提供很好的前提。
4.3 输出误差法
频域输出误差法是利用牛顿-拉夫逊法[7]对极大似然函数优化的算法。极大似然函数一般是待辨识参数的函数,假设其形式为J(θ),对J(θ)进行泰勒展开如下:
(21)
θk+1=θk+Δθ
(22)
(23)
(24)
其中:θ为待辨识模型参数向量,k表示当前的迭代步数,M和N分别是在θk的基础上计算得到的系数矩阵。式(24)即为牛顿-拉夫逊法给出的待辨识参数迭代算法。其中M矩阵为极大似然函数J(θ)对待辨识参数向量的二阶导数矩阵,其形式复杂,数值计算耗时,不适用于数值迭代。比较实用的迭代算法是一种改进的算法,这种算法将M矩阵做了近似处理,以纵向短周期模型为例,其最大似然函数为:
(25)
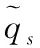
(26)
(27)
(28)
这种方法称为改进的牛顿-拉夫逊方法。在数值迭代过程中,需要不断的对M矩阵求逆,尽管M为对称矩阵,但是由于数值误差的累积作用,迭代过程中,会出现M矩阵的各个特征根量级差别较大,产生由于数值误差而引起的奇异现象,导致迭代发散。因此在程序中还应当采取迭代控制来保证M矩阵求逆顺利进行。采用Levenberg-Marquardt方法可以解决这种数值发散问题。该方法通过增大M矩阵的主对角元素值的大小来改善矩阵的奇异性,使矩阵求逆更加容易。具体方法是:
M-1=(M0+kA)-1
(28)
其中:M0为原信息矩阵,k为非负标量,A为一个正定矩阵,通常取为单位矩阵。k的取法有很多种。在A取为单位矩阵的情况下,建议取为M0矩阵所有元素的平均值的绝对值,即:
(29)
采用这种方法改进后,输出误差法在保证迭代效率的前提下,解决了迭代过程容易发散的问题,取得了较好的效果。
5 算法应用
频域输出误差法具有良好的迭代性能,但对初值的敏感性较高,使用方程误差法和单纯形法得到的初值进行迭代,输出误差法可计算得到精确的最优参数解。计算流程如图3所示。

图3 计算流程图
以某型电传飞机气压高度11 km 、马赫数0.9的试飞数据为例进行辨识。该型飞机的典型试飞数据时间历程如图4所示。按式(2)的纵向短周期模型,使用方程误差法、单纯形法和输出误差法进行参数辨识计算,获取[a0,a1,b0,b1,c0,c1,τ1,τ2]等参数值,再进一步求取式(2)中传递函数的特征根,即可获得该型飞机在气压高度11 km、马赫数0.9的纵向短周期无阻尼自频率ωsp、阻尼比ζsp和时间延迟τe。拟配得到的结果如图5所示,飞机的纵向短周期响应和低阶等效系统的响应重合度较高。飞行品质指标计算结果如表1所示,飞行品质指标与设计值相符,辨识结果合理有效。
以某型电传飞机气压高度5 km 、马赫数0.80的飞行状态下的试飞数据为例,进行横航向低阶等效系统参数辨识计算,辨识结果如图7所示。飞机的横航向响应和低阶等效系统的响应重合度较高。根据辨识结果计算飞机的横航向荷兰滚模态无阻尼自然频率ωdr、阻尼比ζdr、滚转模态时间常数τR等,计算结果如表2所示,飞行品质指标与设计值相符,辨识结果合理有效。

图4 某型飞机纵向短周期模态时间历程

图5 某型飞机纵向短周期模态拟合结果
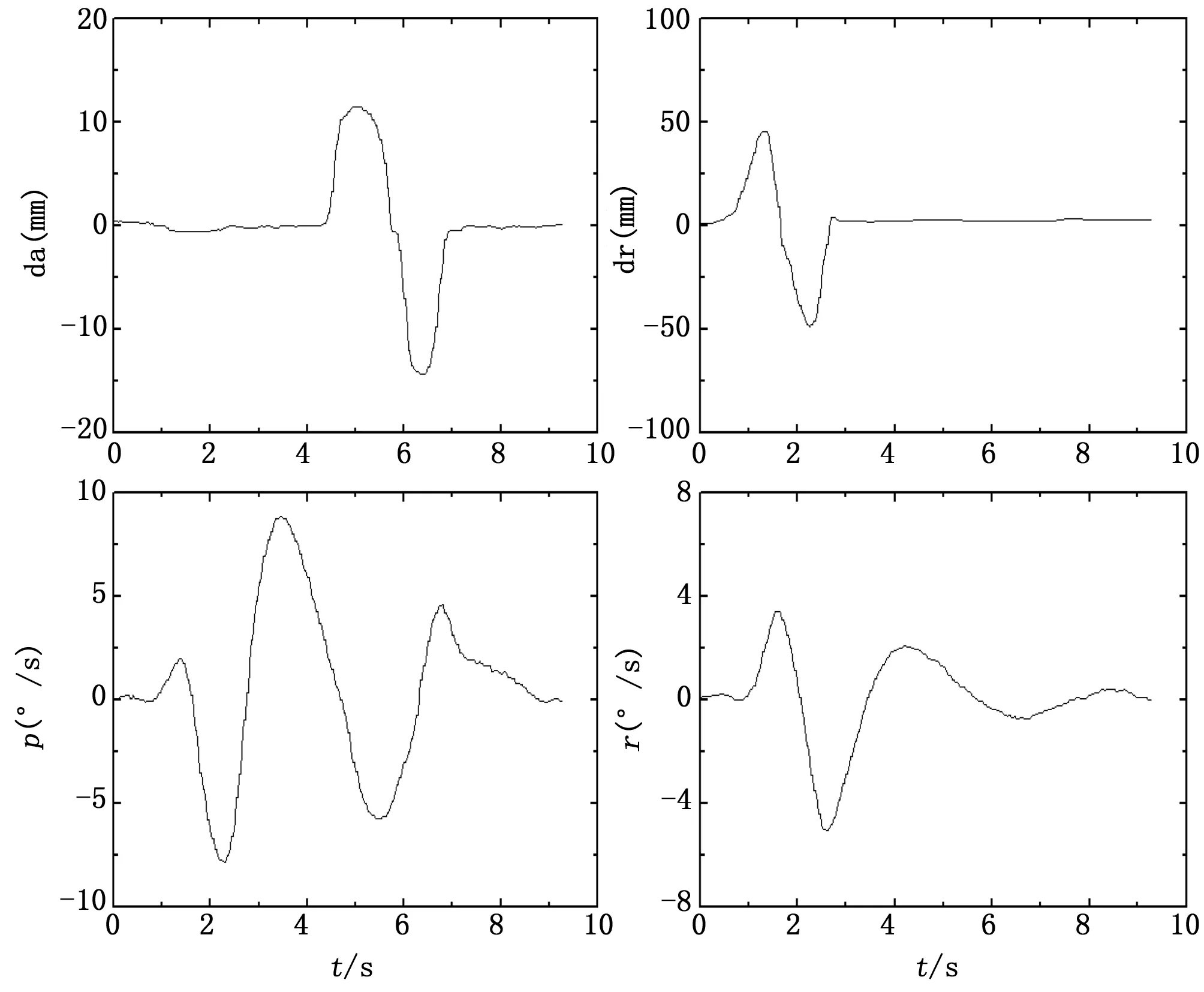
图6 某型飞机横航向时间历程
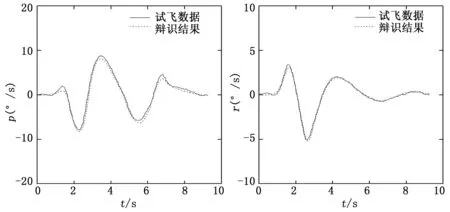
图7 某型飞机横航向辨识结果

飞行品质指标设计值参数辨识值ωsp(rad/s)2.0~3.02.75ζsp0.75~0.850.80τe(ms)100~150118
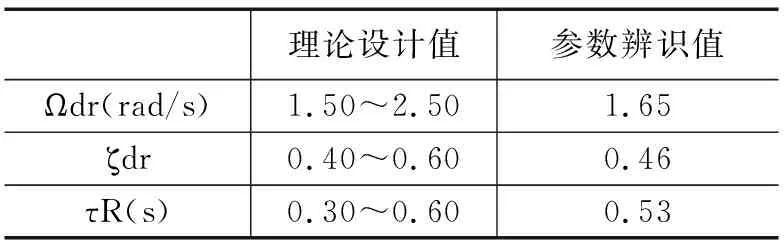
表2 横航向飞行品质辨识结果
6 结论
本文提出了实用的低阶等效系统模型,采用频域相关性分析方法确定辨识频率范围,采用高精度有限傅立叶变换方法对试验数据进行频谱分析,综合运用频域方程误差法、输出误差法和单纯形法,对某型电传飞机的低阶等效系统模型进行参数辨识,准确地计算了该型飞机的飞行品质指标。本文采用的方法为电传飞机飞行品质的评定提供了有效的技术支持[8-11]。
