自由飞行下基于集成学习的概率型冲突探测算法

蒋旭瑞，吴明功，温祥西，霍丹，张怀中

(1.空军工程大学 空管领航学院，西安 710051)(2.国家空管防相撞技术重点实验室，西安 710051)(3.中国人民解放军95133部队，武汉 430000)

0 引 言

近年来，传统的航路航线飞行越来越难以满足日益增长的飞行需求，空域资源利用率较低。自由飞行[1]概念的提出可以解决此问题：飞行员在保持安全间隔的前提下，自由选择航线和速度使飞行代价最少。该运行模式大幅提高了空域利用率，节省了飞行时间，节约了燃油消耗，但同时也给空中交通安全带来了巨大压力。航空器不按照航路航线飞行，无法事先从飞行计划中发现冲突后预先调配，只能通过判断航空器间位置关系实时探测冲突。因此，研究一种具有处理多目标能力的实时冲突探测技术尤为关键。

国内外学者围绕自由飞行条件下的冲突探测展开了大量研究。国外，Sameer Alam等[2]提出了多种冲突探测技术的集成方法，并利用数据挖掘技术识别该方法误报和漏报的隐性特征；CEV Daalen等[3]使用概率流理论求解了总体飞行冲突的概率上界；Marco Porretta等[4]提出了一种最大程度利用飞机意图信息和航迹预测模型的冲突探测算法，能够在解脱中考虑飞机性能；Damien Jacquemart等[5]提出了用马尔科夫链模拟飞机运动轨迹，并使用重要抽样方法计算冲突概率。国内，崔德光等[6]、梁海军等[7]、刘洋等[8]提出了冲突概率的近似解析算法；赵元棣等[9]提出了基于K-近邻(KNN)的冲突探测算法，利用KNN方法建立距离矩阵，并通过冲突判定规则进行探测；石磊等[10]提出了基于布朗运动的总体冲突探测算法。以上算法具有一定局限性：①部分模型对多目标处理复杂；②部分算法人为设置告警阈值，主观性大；③计算精确度不高，虚警较高甚至存在漏警；④对于转弯过程不适用。

飞行冲突探测的实质是一个二分类问题：存在冲突和不存在冲突。机器学习分类算法可以解决这一问题，但主要缺点是：对模型拟合不好、分类准确性不高，存在虚警现象。

为了提高冲突探测准确率，降低虚警和漏警率，本文从提高分类器性能的角度出发，提出基于集成学习的冲突探测算法。在训练各弱分类器后，以支持向量机(SVM)作为第二级分类器，通过Stacking策略形成分类效果好的强分类器，提升分类器性能。此外，该探测算法在分类器训练中加入转弯信息的特征，适用于路径中包含转弯的飞行过程。以期通过以上方法为自由飞行条件下的多机实时冲突探测提供思路。

1 数据集产生

在基于集成学习的飞行冲突探测模型中，需要大量飞行数据用于训练与测试，而实际飞行中冲突很少，导致负类样本(冲突样本)稀缺影响分类效果。通过对飞机运动模型和保护区模型建模，对飞机冲突场景进行仿真，收集飞行样本并判断冲突情况。

1.1 飞机运动模型

飞机在自由飞行时，航迹受雷达探测精度、风等不确定因素的影响，不能认为是沿直线飞行的，飞机运动模型需对若干不确定干扰因素建模。大量研究结果表明，预估航迹的误差是由许多微小而独立的随机变量组成的，且整体误差满足均值为零的Gauss随机分布[9]，其运动方程可以表示为

(1)

式中：X(t)为t时刻飞机的位置；u(t)为t时刻飞机的空速；ω(t)为均值是0的高斯分布的随机变量。

设t时刻飞行方向在水平面的投影与惯性坐标系x轴正向夹角为θ(t)，则飞机运动方程可以表示为如下随机微分方程形式：

dX(t)=u(t)dt+R[θ(t)]∑dB(t)

(2)

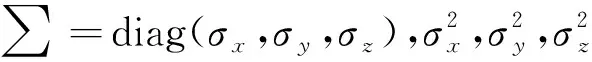
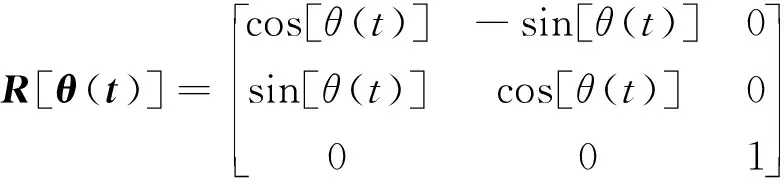
1.2 保护区模型

针对飞机预估航迹存在不确定性误差的情况，细微的外界干扰也可能影响探测结果。因此，不能笼统地按照飞行间隔规定判断是否存在冲突，而应为飞机划设更加精细的保护区。目前应用比较广泛的有模型E和模型V，本文采用椭球模型E(如图1所示)。模型E冲突域可以表示为

(3)

式中：(x0,y0,z0)为椭球中心目标机坐标，(x,y,z)为潜在冲突机坐标。为了符合ATC标准，取椭球体的长焦距a=5 n mile，短焦距c=2 000 ft[10]。

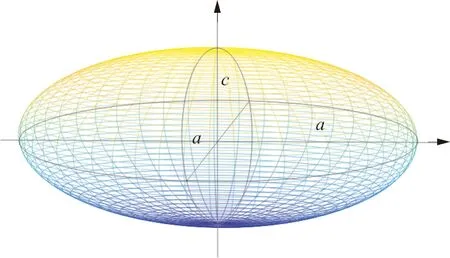
图1 E模型冲突区域

以上模型用于判断飞机在向前看时间内是否存在冲突，其流程为：在向前看时间t的任一时间步长内，任意两架飞机位置关系不满足保护区的约束，则认为这两架飞机存在总体飞行冲突，从而判定多机飞行冲突。大量实证表明，因误差的积累作用，上述误差的建模在15 min内与实际情况基本相符，适用于中、短期冲突探测。

2 集成学习

2.1 Stacking集成学习法

与Bagging和Boosting[11-12]集成学习法不同，Stacking[13]引出了元学习(meta learning)的概念，是一种用于集成不同类型学习器的集成学习法。其基本思想是：根据基本分类器中的分类结果创建元数据集(meta dataset)，用元数据集代替特征量，训练出第二级分类器。通常，单个分类器选择得当，集成学习分类效果相较于单个分类器提升显著。Stacking方法可以表述为以下五个步骤：

步骤1 将原始数据集分成三部分；

步骤2 在第一部分数据集上训练多个弱分类器，获得第一级基本分类器；

步骤3 将第二部分数据集分别在基本分类器中测试，获得不同形式的类别输出，并将输出结果组成元数据集；

步骤4 选择合适的分类算法，在元数据集上训练出第二级分类器；

步骤5 将第三部分数据集作为测试集重复上述训练过程，获得最终分类结果。

各个分类器的参数设置差异越大，分类效果越理想。若基本分类器的分类准确率低于50%，则集成学习将失去价值[14]。

2.2 SVM元分类器构造与后验概率

SVM是一种优秀的二分类机器学习算法，具有良好的推广能力和避免收敛到局部极小点等优点，已在面部识别和网络异常检测等多领域被成熟应用。本文选择SVM作为二级分类器。

假定n个样本的训练集合D={(xi,yi)|i=1,2,…,n}，x∈Rn，y∈{+1,-1}能被一个超平面没有错误的分开，求解广义最优分类超平面，可转化为

(4)

式中：C为惩罚因子，通过参数C实现对错分样本的惩罚。

通过构造拉格朗日函数求解，其对偶形式可以表示为

(5)

根据式(5)可以求得决策函数：

f(x) =sgn{(w·x)+b}

(6)

标准的SVM通过决策函数f(x)与0的关系，判断样本种类为正例或负例，是标准的硬输出。文献[15]提出通过Sigmoid函数把SVM的硬判断输出映射到[0,1]，实现后验概率输出，其形式为

(7)

式中：f为SVM的标准输出结果；P(y=1|f)为在该输出下判断为正样本的概率。

A和B决定了Sigmoid函数的平滑程度及估计μ的准确度，可通过最小化训练数据的负对数似然值得到：

(8)

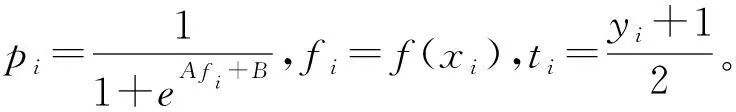
3 集成学习冲突探测模型

为了构造元分类器，本文将仿真获得的原始飞行数据集分为三部分，第一部分用于训练基本分类器，第二部分用于构造元数据集，第三部分用于测试。在基本分类器的选择上，本文采用不同学习算法相结合的异质分类器。选择KNN、朴素贝叶斯、BP神经网络和SVM作为基本的学习算法。其基本流程如图2所示。

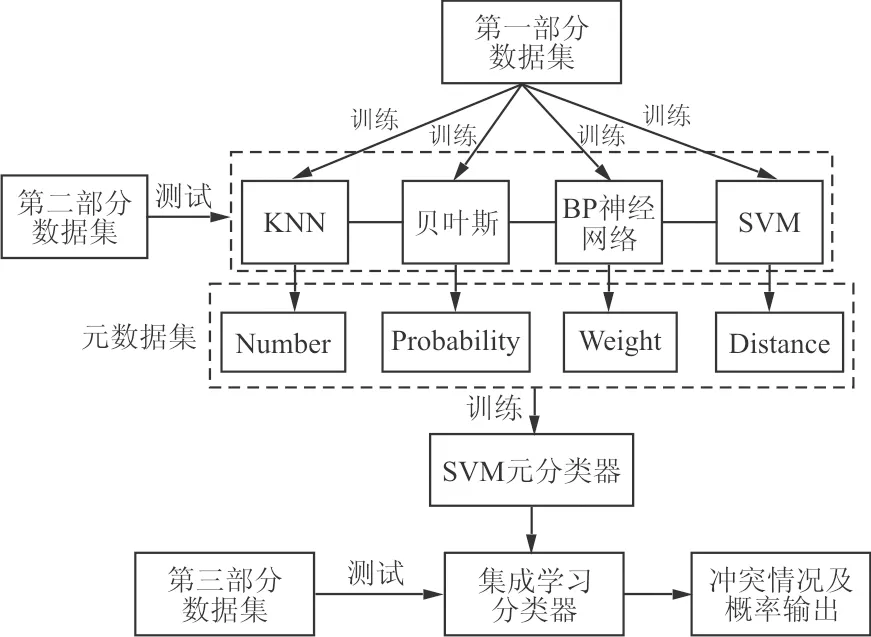
图2 集成学习冲突探测模型

四个基本分类器的输出分别为“属于正负类的样本点数量”、“后验概率”、“权值”以及“点到超平面的距离”。它们构成了元数据集，用于训练SVM元分类器，这个元分类器将多个基本分类器的分析结果进行二次学习，预测出最终冲突情况，并输出飞行冲突概率。单一分类器的学习过程如图3所示。

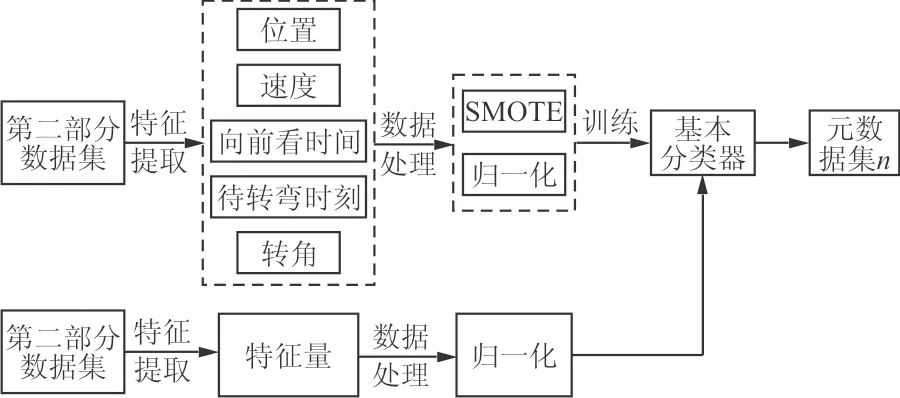
图3 单一分类器获取元数据集流程

(1) 数据采集

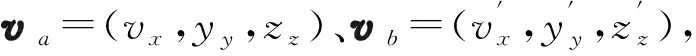
(xr,yr,zr,vxr,vyr,vzr,t)

若需预测飞行中的转弯阶段，则训练样本中需提取两机转弯时刻t1、t2和转弯角度θ1、θ2，构成11维特征量：

(xr,yr,zr,vxr,vyr,vzr,t,t1,t2,θ1,θ2)

(2) 数据处理

在容量限制内，空域中自由飞行的飞机发生冲突是小概率事件，收集的样本中正样本(无冲突)占多数。为了避免样本数量不平衡影响冲突探测效果，应使正、负样本数量大致均衡。采用SMOTE重采样方法提升处理不平衡样本的分类能力，具体做法为：通过在邻近的负类样本间插入虚拟样本，以减少过适应现象的出现[11]。另外，为了避免各维度间数据分布差异过大影响分类效果，将数据进行归一化处理：

(9)

式中：X为样本特征量；Xmin和Xmax分别为变量X，取最大值和最小值；Y∈[-1,1]为归一化后的变量。

4 仿真分析

数据采集阶段，模拟双机飞行，记录飞机特征量，根据飞机航迹预测与保护区模型判断向前看时间t={t|t∈(0,15],t=N*}内是否存在飞行冲突，获得类别标签(存在冲突为-1，不存在冲突为1)。以直线飞行和转弯飞行两种情况作为仿真场景，分别选择2 000组、300组和100组数据作为第一、二、三部分数据集。

4.1 直线飞行场景

将第三部分数据集输入各分类器后，各基本分类器分类结果如表1所示。

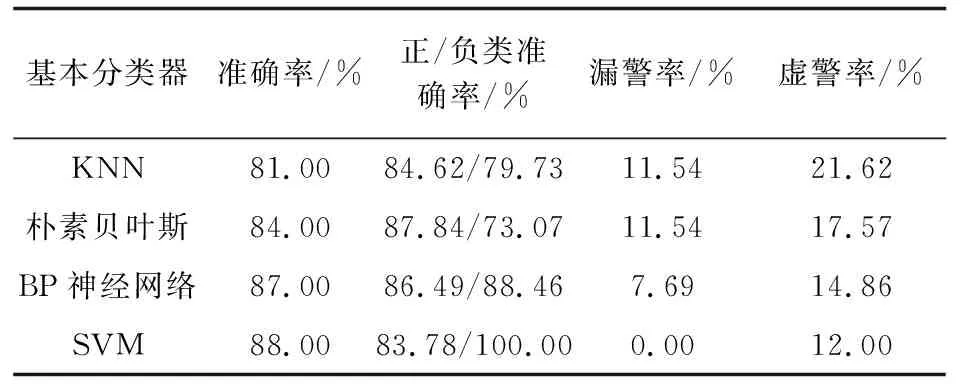
表1 各基本分类器识别率

从表1可以看出：四种分类器识别准确率接近，且为80%～90%，分类准确率从高到低依次是SVM、BP神经网络、朴素贝叶斯和KNN。特别地，SVM基本分类器在参数调整后能准确识别负类样本，无漏警，将其作为二级分类器效果较好。虽然四种单一分类器对冲突探测识别率较高，但虚警率为10%～25%，甚至存在漏警(10%左右)，而探测准确率直接关系到飞行安全。为了提高冲突探测准确率，本文采用Stacking集成学习方法提升分类器性能。测试数据集在集成学习分类器中的分类结果如图4所示。

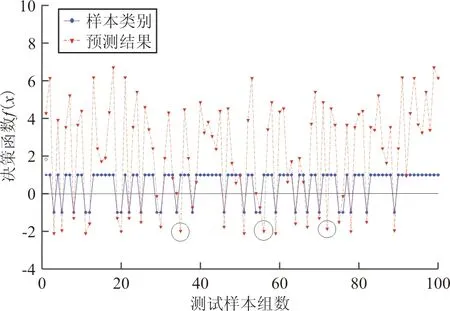
图4 直线飞行冲突探测结果

图4中，圆表示样本类别(+1/-1)；三角为决策函数值，表示样本在SVM元分类器中分类结果。决策函数由式(6)给出，当f(x)>0时，分类结果为+1；反之，f(x)<0时，分类结果为-1。图4中圈出了判断错误的样本，共3个，均属于虚警，无漏警现象，元分类器识别直线飞行冲突准确率为97.00%，虚警率为4.05%，探测效果较好。

4.2 转弯飞行场景

在自由飞行条件下，飞机通常难以通过直线飞行到达目的地，而转弯飞行是冲突探测的难点。在集成学习中，将转弯信息作为特征量训练基本分类器，并将训练好的集成学习分类器在飞行前封装在飞机冲突探测系统中。进入自由飞行空域后，只要输入各飞机当前位置、速度信息，预计转弯时刻及转弯角度，即可预测指定向前看时间内的飞行冲突。该算法是协作式的，需要掌握全面的空中态势信息。对100组转弯飞行数据进行测试，结果如图5所示。

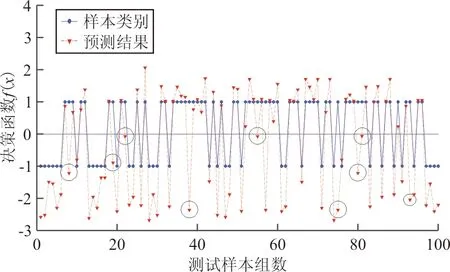
图5 转弯飞行冲突探测结果

图5中，100组测试样本，探测准确率为91.00%，虚警率为22.50%，无漏警现象。可以看出：基于集成学习的冲突探测算法在转弯飞行中仍然适用，但探测效果要劣于应用于直线飞行的探测中。

为了验证集成学习方法对模型探测效果的性能提升，将四种单一分类器作为对照组，绘制接收机工作特性曲线(ROC曲线)，得出虚警率与检测概率的关系如图6所示。ROC曲线应用在分类算法性能评估中，曲线上的点代表同一分类算法在阈值不同时的虚警概率和检测概率，是衡量分类性能的重要指标。

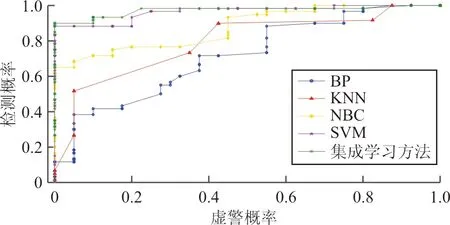
图6 ROC曲线

以虚警概率为x轴，检测概率为y轴，绘制六机预测航迹(如图6所示)，曲线1～5分别为BP神经网络、KNN、朴素贝叶斯、SVM基本分类器和集成学习分类器分类结果绘制成的ROC曲线。可见，在冲突探测模型中，基本分类器性能由强到弱排序依次为：SVM，朴素贝叶斯，KNN，BP神经网络。在相同检测概率的情况下，集成学习算法的虚警率低于其他基本分类算法；相同虚警概率的情况下，集成学习算法检测率最高，表明了集成学习算法能有效地降低飞行冲突探测的虚警率，提升探测准确率。

为了验证集成学习分类器输出冲突概率的有效性，更直观地反映冲突情况，本文对六机飞行场景进行仿真，其航迹如图7所示。

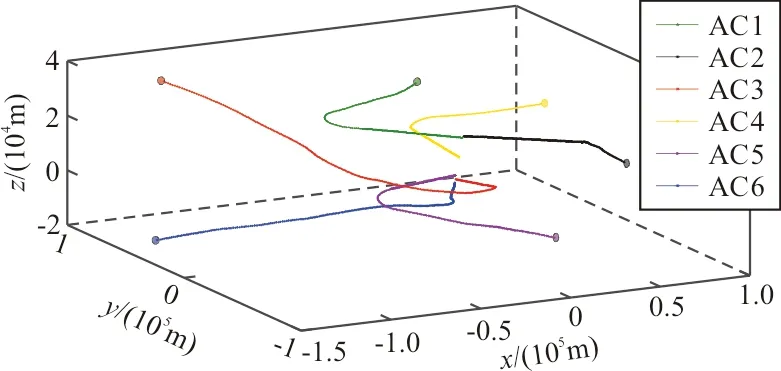
图7 六机预测航迹

图7中，各飞机冲突矛盾突出，将该组数据作为测试样本，在集成学习分类器中预测向前看时间6 min内的飞行冲突，并根据式(7)计算冲突概率。结果可用矩阵N6×6表示，“0.00#”表示小数点后第2位数值小于5。

ABCDEF A0B99.210C43.750.00#0D35.8532.1912.850E0.00#0.00#93.3228.540F0.00#0.00#97.520.00#99.650

N6×6是对角线为0的上三角矩阵，各元素代表对应飞机间的冲突概率，当冲突概率大于50%时认为存在飞行冲突。由集成学习冲突探测模型计算得出六架飞机间存在冲突的飞机对为：A和B，C和E，C和F，E和F，与实际冲突情况一致，探测效果较好。

5 结 论

本文将冲突探测问题考虑为二分类问题，通过集成学习方法提升飞行冲突探测准确率。相较于单一基本分类器探测准确率显著提升，虚警概率大幅下降。基于集成学习的冲突探测算法适用于空中态势复杂的多机转弯飞行，探测准确率较高。该方法的提出为空管自动化系统中的冲突探测问题提供了理论参考，下一步将利用实际飞行数据进行试验。