多机空战指挥引导不平衡目标分配方法研究

高阳阳，余敏建，杨杰

(空军工程大学 空管领航学院，西安 710051)

0 引 言

在多机协同对抗的网络化现代空战中，对敌我战机的引导配批是多机空战指挥引导的重要环节，合理科学地进行引导配批能更好地发挥多机空战的整体效能。

从理论角度，对敌我战机的引导配批问题属于目标分配问题。目前，对于目标分配问题国内外进行了相关的研究。在国外，J.C.F.Cabrera等[1]、S.Moon等[2]研究了对美国空军无人机协同作战目标分配问题；Aleksandar Jevtic等[3]研究了无人机协同控制与任务分配问题。在国内，Lee Z J等[4]在武器目标分配方面展开了研究；肖金科等[5]采用人工免疫算法解决了大规模区域反导目标分配问题；崔亚妮等[6]提出了一种多无人机时敏任务动态分配算法，实现战场环境下多架无人机对多个时敏目标的打击；王然辉等[7]采用遗传算法解决了对地打击武器—目标分配问题；夏维等[8]采用改进型多目标粒子群优化算法解决了武器—目标分配问题；宋遐淦等[9]采用改进的模拟退火遗传算法解决了协同空战目标分配问题。

但以上算法存在如下问题：不平衡目标分配问题中经常会遇到加入战场和退出战场等情况，采用上述方法处理动态不平衡目标分配问题时，难以保证算法的时效性，且搜索效率低，容易出现早熟收敛现象。

匈牙利算法是目前公认的一种能有效解决目标分配的算法，在解决小规模目标分配问题时具有运算速度快、可靠性好等特点。然而大量的数据试验表明，匈牙利算法在处理某些特殊的数据时会不收敛而无法找到最优解，且耗时、不稳定，当目标分配问题的矩阵规模较大时，通常会出现不收敛的情况。

基于多机空战的实际考虑，本文将多机空战的指挥引导配批问题，分为小规模配批问题和大规模配批问题，分别采用匈牙利算法和进化匈牙利算法进行目标分配，并进行仿真分析，以期为解决多机空战指挥引导不平衡目标分配问题拓展研究思路。

1 目标分配模型

1.1 目标分配的概念

考虑战机数量，目标分配有两种方式，一种是平衡目标分配方式，另一种是不平衡目标分配方式[10]。

(1) 平衡目标分配方式

平衡目标分配方式是指空战中，敌我双方兵力一致，且战机能力相当时，根据战场态势，将敌我战机以“一对一”进行分配的方式，能够有效确保作战兵力使用的效率，防止火力浪费。如图1所示。

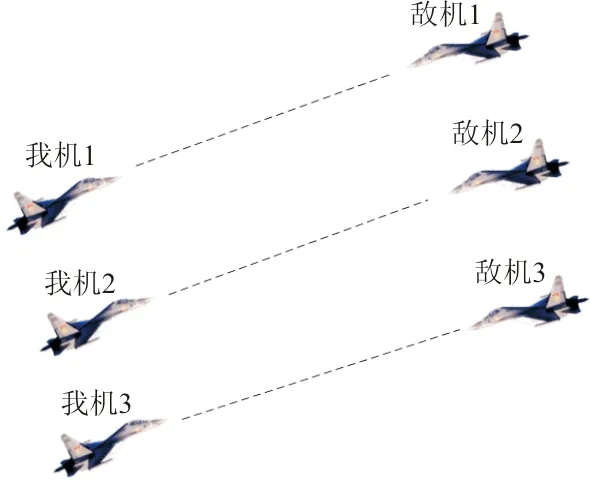
图1 平衡目标分配方式

空战中，双方战机在执行作战任务中导致的战损，或者是战术性的加入或退出战场，都会导致空战态势发生变化。为了紧跟战场态势，确保掌握战场主动，必须对之前的目标分配结果做出及时调整，应根据新的战场态势进行再次分配。由于作战力量发生了改变，平衡目标分配方式不再适用于新的战场态势，由此转为不平衡目标分配方式。由此可见，平衡目标分配方式通常为最初的分配方式。

(2) 不平衡目标分配方式

在实际作战中，平衡目标分配方式只是一种比较理想的情况，通常情况下，双方战机数量是不相等的。在我方探测到敌方来袭兵力时，为了确保战争的胜利，在不浪费物资的前提下通常会派出较敌方更多的战机，以求在兵力上进行压制，取得作战优势。例如，我机数量n大于敌机数量m，这就会出现多架我机同时打击一架敌机的情况，或者是在经过敌我空中交火后形成的剩余战机数量不等的情况，这时应进行不平衡目标分配，如图2所示。

图2 不平衡目标分配方式

1.2 多机空战指挥引导目标分配模型

通常情况下，对多机空战目标分配需要综合考虑战机机型、战机挂载导弹数量、挂载导弹性能以及战机的电子干扰等能力。本文主要是针对三代机的多机空战指挥引导问题进行研究，考虑到三代机性能和导弹挂载能力的差别相对于战机数量的差异对空战的影响很小；此外，在实际空战中，我方在探明来袭敌机的情况下，通常会派遣综合性能高于敌方战机的我机进行空战。因此，本文对多机空战指挥引导问题进行简化处理，做出如下假设：

①空战中我方战机机动性能优于敌机；

②敌我战机的电子干扰能力相当，即不考虑敌我战机的电子对抗；

③考虑到三代机不具备多目标攻击能力，假设敌我战机挂载导弹数量满足作战任务需求，且对目标实施攻击只需要一枚导弹，即在对所分配的目标实施攻击后剩余导弹可用来攻击下一次分配的目标。

根据以上假设，在多机空战的指挥引导目标分配中，只需要考虑空战中的敌我战机数量，由此进行指挥引导目标分配建模。假设空战中有敌机m架，我机n架，我机只能同时对一架敌机进行攻击，我方战机组成机群W={Wi,i=1,2,…,n}，敌方目标机组成机群D={Dj,j=1,2,…,m}，其中Wi表示我方第i架战机，Dj表示敌方第j架战机，为了取得空战胜利，通常在兵力使用时应对敌方兵力构成优势，因此，应满足n≥m，则多机空战指挥引导目标分配问题的模型可以描述为

(1)

(2)

(3)

满足

(4)

式中：C=(Cij)n×m表示评价矩阵，Cij为第i架我机对第j架敌机构成的空战指挥引导优势值数值；X=(Xij)n×m表示目标分配的解矩阵，Xij值为1时，表示已经把第j架敌机分配给我方的第i架战机，Xij值为0时，表示未把第j架敌机分配给第i架我机；Z为目标函数，表示我方机群总的指挥引导优势值，反应我方机群总的空战态势优势，给出分配解X以使总指挥引导优势值Z最大。约束条件(2)和(3)分别表示我方一架战机只能攻击一架敌机和一架敌机可以同时被我方两架战机攻击，体现了多机空战指挥引导目标分配的特点。

2 基于匈牙利算法的多目标任务分配

2.1 匈牙利算法

匈牙利算法是由库恩(W.W.Kuhn)在1955年提出的，是一种关于指派问题的求解方法。匈牙利算法引用了匈牙利数学家康尼格(Dénes König)的一个关于矩阵中独立0元素个数的定理：矩阵中独立0元素的个数等于能够覆盖所有0元素的最少直线数[11]。

尽管具有多目标攻击能力的四代机、五代机的研制进度加快，也有部分四代机装备部队，但是我国现阶段空战的主战飞机仍然是不具备多目标攻击的三代机。在实际空战中，为了达到作战目的，保证作战效果，我方通常采取大于或等于敌方战机数量的兵力进行作战。在这种情况下的多机协同攻击多目标的任务分配即是一种典型的组合优化问题，也是一种单对单的目标分配问题，适合采用匈牙利算法进行计算和求解。在一般的匈牙利算法目标分配模型中，主要通过对评价矩阵的计算处理得到分配结果[12]。匈牙利算法的一般实施步骤如下：

第一步：对空战敌我战机进行随机编号；

第二步：以敌机的属性和敌我空战态势为主要依据进行态势评估，构建评价矩阵；

第三步：对评价矩阵进行线性变换，使各行各列中出现0元素为止(每行每列分别减去该行该列中的最小元素)；

第四步：由调整后的评价矩阵得到最优分配结果。

评价矩阵中的元素值是当前态势下我机相对于敌机的指挥引导优势值，评价矩阵的行号和列号分别代表我机和敌机的战机编号，例如：第一行第一列处的元素是我机“1号”对敌机“1号”的指挥引导优势值，第一行数据就是我方“1号”战机分别对于敌方所有战机的指挥引导优势值，其他数据定义也是如此。

2.2 进化匈牙利算法

进化匈牙利算法[13]是由J.H.Holland提出的，采用进化算法可以有效地解决目标分配问题，但计算速度随着维数的增长显著下降，无法较好地满足战场实时性的要求。

不平衡目标分配问题可以变换为平衡目标分配问题进行解决，因此对基于三代机的多机空战指挥引导目标分配问题可以看作是“单对单”的分配方式，即在目标分配的解矩阵中表现为每行每列均只有一个“1”，“1”代表对应战机号进行目标分配，“0”代表对应战机号未进行分配。本文采取将匈牙利算法和进化匈牙利相结合的方式进行大规模目标分配的处理，算法初始种群由两部分组成，一部分是由匈牙利算法求解得到的解矩阵，该解矩阵对应的目标分配方案通常不是最优，因此再随机生成0-1矩阵替换解矩阵中的部分行和列，由此组合后的矩阵作为初始种群，通过交叉、复制及变异等操作得到最终的分配结果，既可确保分配结果的最优又可确保算法收敛的时效性。算法使用的变异算子是随机的交换结果矩阵的两行或两列，如下所示：

将第一行和第二行交换：

将第二列和第四列交换：

算法流程为

步骤1 对空战中敌我双方战机数量进行判断并随机编号。若敌我双方战机数量都不超过4架，则可以直接使用单纯的匈牙利算法进行计算；若战机数量大于4架，认为是大规模目标分配问题，采用两种算法相结合的方式进行处理。

步骤2 在处理大规模目标分配问题时，首先对评价矩阵采用匈牙利算法来处理，得到对应的解矩阵，然后随机生成若干个对应的0-1矩阵，将生成的0-1矩阵和得到的解矩阵一起作为算法的初始种群。

步骤3 计算每个个体在种群中的适应度，并进行复制、变异。复制：保留父代种群中适应度高的优良个体并添加到子代种群中，并删除父代种群中适应度差的个体；变异：首先从父代种群中随机选择一个个体进行变异处理，即对其中的任意两行或两列进行交换后得到新的个体，然后将新的个体添加到子代种群中。

步骤4 首先重复步骤3，增加进化代数，直至达到最大进化代数为止，然后对得到的种群中的个体进行选择，最优的个体即为所要求的解，其对应的目标分配结果即是最优的分配方案。

2.3 动态目标分配的处理

空战中，敌我双方参战兵力会由于战机的损伤或退出发生变化，因此目标分配将是动态进行的过程。敌我双方空战的态势信息是通过评价矩阵体现的，因此可以通过对评价矩阵的处理来反映战场形势的变化。

(1) 战机退出战场的情况

当战机退出战场时，其对应的评价矩阵中的行或列应该被删除，但是为了保持评价矩阵的完整性，使评价矩阵能够用于算法的计算处理，通常需要采用补边法(将退出战场的敌机对应评价矩阵的行或列元素值改为0)，既确保了评价矩阵的完整性，又确保了改动的元素值不影响正常的目标分配。具体方法如下所示：

当前的评价矩阵为

我方2号战机退出战场后的评价矩阵为

敌方4号战机退出战场后的评价矩阵为

(2) 战机加入战场的情况

当战机新加入战场时，战场中战机数量发生变化，评价矩阵也随之变化，通过地面信息平台对新加入的战机进行态势评估后建立新的评价矩阵，此时的评价矩阵的行数和列数不相等，采用前述补边法进行处理。具体方法如下所示：

当前的评价矩阵为

我方6号战机加入战场后的评价矩阵为

敌方6号战机加入战场后的评价矩阵为

3 仿真分析

(1) 战机数量增加

空战中敌我双方战机数量的初始态势有三种情况：我机数量占优、敌机数量占优和敌我机数量相等。但在实际作战中，为了保证作战效果，通常不会出现初始情况下我机数量少于敌机数量的情况，在我机数量占优的情况下，敌机数量增加后可以转化为平衡目标分配问题，在此对敌我战机数量相等的情况进行研究。假设对应的评价矩阵为T4×4

使用匈牙利算法计算处理，得到的结果矩阵为

对应的分配结果为：我机1号攻击敌机3号；我机2号攻击敌机2号；我机3号攻击敌机1号；我机4号攻击敌机4号。

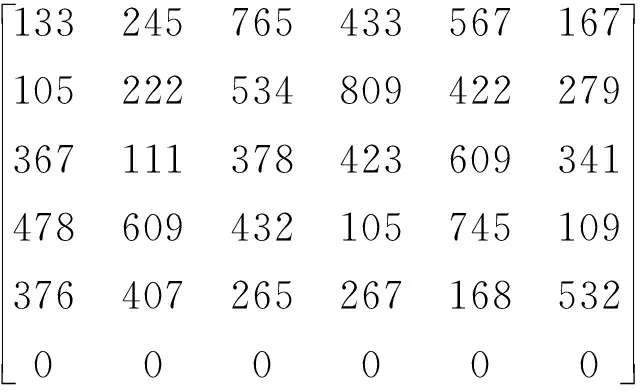
若突然增加战机，则根据补边法对评价矩阵进行改动。在此初始条件下，若敌方增加一架战机，通过分析战场态势，得到新增战机威胁值后，相应的在评价矩阵后加入一列该战机对我机的威胁值，同时需要在评价矩阵下方加入对应的行进行“补边”，原则是不影响正常的目标分配。修改后的评价矩阵为

结果矩阵为

对应的分配结果为：我机1号攻击敌机3号；我机2号攻击敌机2号；我机3号攻击敌机1号；我机4号攻击敌机5号；我机5号攻击敌机4号。

敌方加入后的分配情况如图3所示。

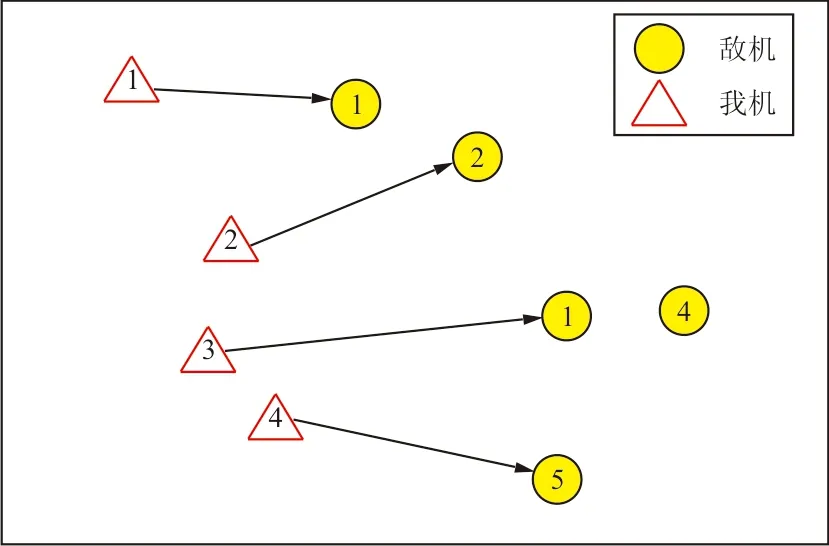
图3 敌方加入后的分配情况

从图3可以看出：分配情况较最初有所变化，且在敌机数量增加后，在分配中出现漏分配的情况(若没有我机攻击敌机4号)，此时指挥员应该根据战场形势对我机进行数量补给，以确保我方在不浪费兵力的情况下占据优势态势。

(2) 战机数量减少

以上述初始条件进行研究，假设对应的评价矩阵为T4×4

结果矩阵为

对应的分配结果为：我机1号攻击敌机3号；我机2号攻击敌机2号；我机3号攻击敌机1号；我机4号攻击敌机4号。

当敌机3号退出战场，采用补边法需对第三列进行修改如下：

结果矩阵为

对应的分配结果为：我机1号攻击敌机3号；我机2号攻击敌机2号；我机3号攻击敌机1号；我机4号攻击敌机4号。

敌方退出后的分配情况如图4所示。

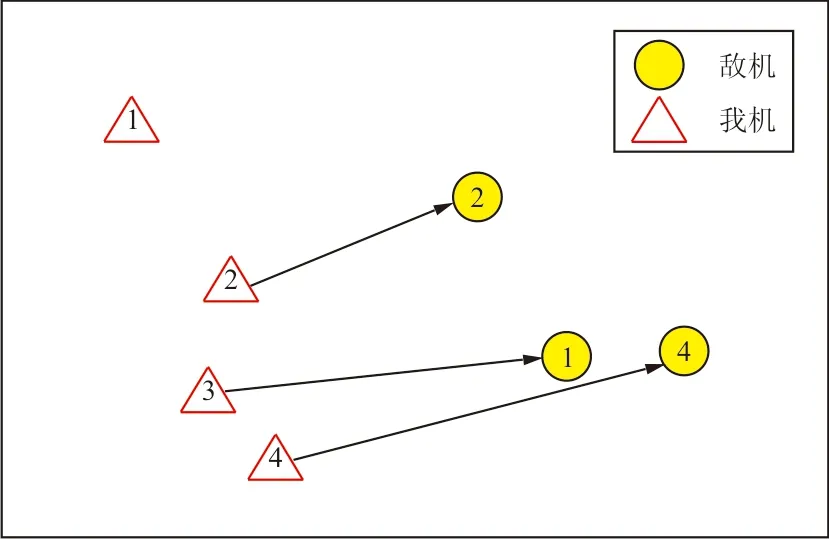
图4 敌方退出后的分配情况

从图4可以看出：在敌机3号退出战场后的目标分配结果中，我机1号没有分配攻击目标，此时可以通过指挥员根据个人意向选择1号对任意敌机进行攻击。

在图4情况下，可以选择我机1号协同2号攻击敌机2号，再分配情况如图5所示。

图5 指挥员个人选择后的再分配情况

(3) 多维目标分配仿真分析

实际空战中，通常是机群作战，双方战机数量较大，为了验证算法在处理多维目标分配时的时效性和可靠性，选取48维不同进化代数的仿真结果进行分析。

评价矩阵由电脑随机产生，评价矩阵中的元素值的大小在0到1之间并且满足约束条件。进化代数设置为100至1 000代，每隔100代记录一次数据，采用改进的进化匈牙利算法处理目标分配问题，结果如表1所示。

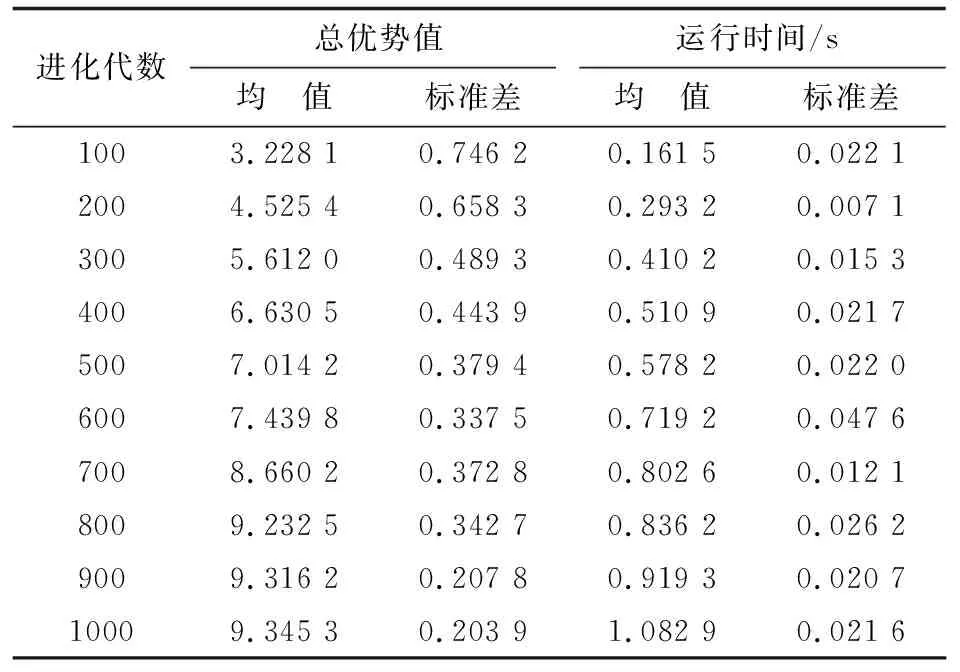
表1 48维评价矩阵进化代数数据分析表

从表1可以看出：随着进化代数从100代到1 000代，评价矩阵总优势值不断增加。由于在改进的进化匈牙利算法中加入了交叉、变异操作，使种群的多样性得到增强，进化代数达到700代后才不断趋于稳定，有效防止了过早收敛现象的发生。同时，算法运行时间也随着进化代数的增加而不断增加，但是基本都能保持在1 s内，能够满足战场实时性要求。该仿真结果表明了算法具有较好的时效性和可靠性，能满足多维条件下的目标分配处理。

4 结 论

(1) 分配组数小于5组为小规模问题，可以直接用匈牙利算法进行计算，计算时间快且分配结果准确。分配组数大于等于5组时为大规模配批问题，采用进化匈牙利算法，有效避免了匈牙利算法在处理维数较大问题时运算时间长和无法收敛的问题，有效确保了目标分配方案的整体指挥引导优势。

(2) 本文提出的新的多机空战不平衡目标分配方法具有较好的时效性和可靠性，能满足多维条件下的目标分配处理，满足实战需求。