微分算子带一般权第二特征值的上界估计

赵晓苏，钱椿林

(苏州市职业大学 数理部，江苏 苏州，215104)

设(0,1)∈R是一个有界开区间，考虑如下的特征值问题：

(1)

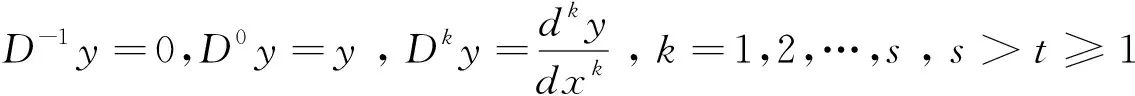
0≤pi(x)≤μ2,i=t+1,t+2,…,s-1，pt+1(x)>0，μ1≤ps(x)≤μ2，

(2)

q1(x)=q2(x)=…=qτ-1(x)=0，1≤τ≤t，ν1≤qj(x)≤ν2，j=τ,τ+1,…,t，

(3)

其中，0<μ1≤μ2，且0<ν1≤ν2。

当s>t≥2时，问题(1)特征值的上界估计已有一些结果①。 在本文中，考虑微分算子带一般权并且左端的最低导数阶数比右端的最高导数阶数恰好高二阶的问题(1)，且s>t≥1，这个问题是微分算子第二特征值的上界不等式②的推广。 运用文献[5]中的方法，对于任意整数s>t≥1的微分算子，得到了问题(1)的用第一特征值来估计第二特征值的上界估计，其估计在微分方程的理论研究和力学的应用中起着重要的作用[6]。

定理1 设λ1,λ2是问题(1)的两个第一、第二特征值，且0<λ1≤λ2，s>t≥1，则有：

(4)

定理2 设λ1,λ2是问题(1)的两个第一、第二特征值，且0<λ1≤λ2，s>t≥1，τ=t, 则有：

(5)

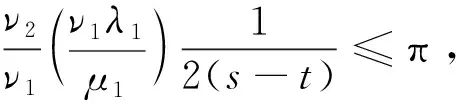
2 定理的证明

设λ1是问题(1)的第一特征值，相应于λ1的特征函数为y1，简记y=y1，且满足：

(6)

利用t次分部积分和式(6)，得：

(7)

利用s次分部积分和式(7)，有：

(8)

利用(2)和(8)，得：

(9)

利用(3)和(7)，有：

(10)

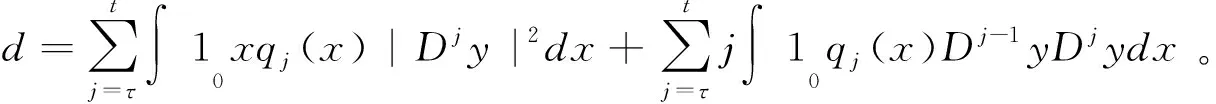
利用分部积分，直接计算得：

(11)

从(11)式知，φ与y带权正交，且满足Dkφ(0)=Dkφ(1)=0，k=0,1,2,…,s-1。

利用Rayleigh定理，有：

(12)

计算得：

(13)

利用分部积分和φ(x)=(x-d)y，有：

(14)

结合式(13)和(14)，得：

(15)

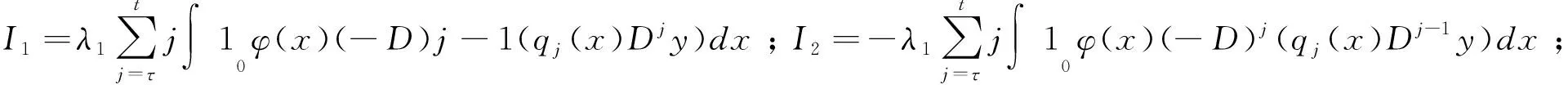
利用式(15)，有：

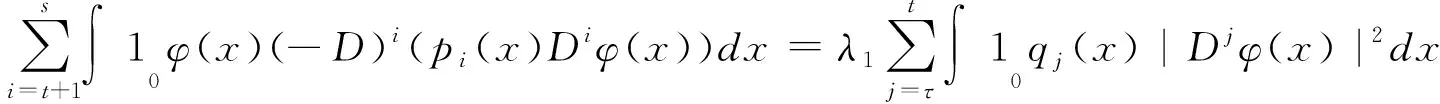
(16)

利用式(12)和(16)，得：

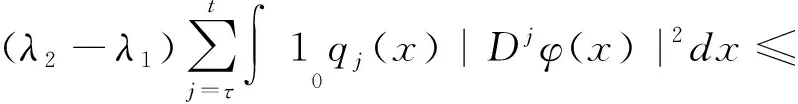
(17)

引理1 设y是问题(1)所对应第一特征值λ1的特征函数，则：

证明 对于(a) 参考现代应用分析卷。

对于(b)，反复运用引理1(a)和(10)，得引理1(b)。

引理2 设y是问题(1)所对应第一特征值λ1的特征函数， 则：

证明 用数学归纳法证明(a). 反复运用引理2(a)和(9)，即得 (b), 参考文献[1]。

引理3 设y是问题(1)所对应第一特征值λ1的特征函数, 则：

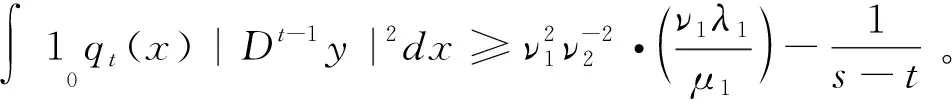
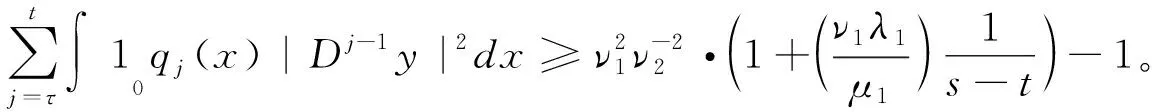
证明 对于(a)，利用Schwarz 不等式、引理2(b)、式(3)和(7), 当τ=t时，得：

当τ

整理后即得 (a)。

对于(b)，利用(7) 、Schwarz 不等式和引理2(b)，有：

对于(c)，在引理2(b)中，取r=i-1，利用式(2)，得：

对于(d)，利用Schwarz 不等式、引理1(b)和引理2(b)，得：

对于(e)，利用Schwarz 不等式、(2)、引理2(b)和引理3(d)，得：

引理4 设λ1是问题(1)的第一特征值,则：

当τ=t时，

当τ

证明 利用分部积分和φ(x)=(x-d)y，得：

(18)

(19)

(20)

(21)

利用式(18)、(19)、(20)和(21)，有：

(22)

利用式(22)和引理3，当τ=t时，得：

当τ

引理5 对于φ(x)与λ1, 则：

证明 利用分部积分和φ(x)=(x-d)y，得：

(23)

利用式(23)，有：

(24)

利用式(10)和(24)，得：

(25)

在引理2(b)中，取r=t+1，利用式(10)、(25)和Schwarz 不等式，当τ=t时，有：

当τ

整理上式即可得引理5。

证明 利用引理4和引理5，从(17)，当τ

(26)

由式(26)即可得到定理1的(4)；

当τ=t时，有：

(27)

由式(27)即可得到定理2的(5)。