方差分析在雷达精度试验数据处理中的应用∗

马 强

（92941部队 葫芦岛 125001）

1 引言

在雷达试验中，精度是试验考核的重要项目之一。雷达精度试验的方法目前主要有基于GPS的校飞方式［1］、跟踪卫星方式［2］、基于精密设备测量的方式［3］和基于ADS-B数据的标校方式［4～5］等四种方法。雷达精度试验主要考核距离、方位、俯仰、速度等项目指标。这些指标结果对不同的雷达会产生不同的影响，对于引导雷达，不能够为其他设备提供准确的目标引导信息，而对于火控雷达，则将影响武控系统是否能够有效攻击目标［6］。影响雷达精度的因素有很多，如与雷达本身、目标特性和空间传输环境等因素［7］。为了判断这些因素对雷达精度产生的影响，可以合理地设置不同影响因素搭配的试验，利用方差分析技术对这些因素进行分析。

方差分析又叫变量分析，是英国著名统计学家费希尔于20世纪初提出的，用于两个及两个以上样本均值差别的显著性检验［8］。在实践过程中，影响系统性能的因素往往很多，利用方差分析可以从这些因素中找出哪种是主要因素，哪种是次要因素，进而对这些因素进行控制，以提升系统的性能。

本文主要运用方差分析方法，以目标海拔高度为例，探究这一因素对雷达距离精度是否产生显著性的影响。

2 方差分析原理介绍

方差分析的基本思想是：通过分析研究不同变量的变异对总变异的贡献大小，确定变量对研究结果影响力的大小。通过方差分析，分析不同的水平变量是否对结果产生了影响。如果产生了显著性的影响，那么它和随机变量共同作用，必然会使结果有显著的变化；如果没有显著影响，那么结果的变化主要由随机变量起作用，和分析的变量关系不大。

2.1 方差分析的三个假定

在应用方差分析时，要求对研究的数据满足如下三个假定：

1）被检验的各个总体都服从正态分布；

2）各个总体的方差相等；

3）从每一总体中抽取的样本是相互独立的。

这三个假定，都可以用统计方法进行验证。对第一个假定可以用正态性检验方法如夏皮洛—威尔克检验［9］方法进行判断，当试验数据不服从正态分布时，可以采用数据转换的方法使之变为服从于正态分布的数据，常用的数据转换方法有平方根转换、反正弦转换、对数转换和倒数转换等方法。对于第二个假定，可以利用方差齐性检验的方法进行验证，方差齐性检验的方法主要有Hartley检验、Bartlett检验和修正的Bartlett检验等方法［10］，当试验数据不满足方差齐性条件时，可以将异常的观测值剔除，但剔除数据时要小心，以免丢失重要信息，也可以将试验资料分成几部分，使每部分具有相同的误差方差。对于第三个假定，可以使试验按随机次序进行，以保证各次试验独立。

方差分析方法是需要在上述三个假定都满足的情况下才能进行。

2.2 单因素方差分析

设单因素A有a个水平A1,A2,…,Aa，在水平Ai(i=1,2,…,a)下，进行ni次独立试验，样本取值为 xi1,xi2,…,xini，它们来自具有相同方差σ2，均值分别为 μi的正态总体 N(μi,σ2)。其中 μi，σ2均为未知，并且不同水平Ai下的样本之间相互独立。

单因素的数据结构模型如下：

在上式中，εij为试验随机误差。方差分析的任务就是对上述模型中a个总体N(μi,σ2)中各 μi的相等性进行假设检验，既有

原假设 H0:μ1=μ2=…=μa

备择假设 H1:μi≠μj，至少有一对这样的 i,j。

单因素方差分析的步骤如下：

在上式中，fT为ST的自由度。可以将ST分解：（1）单因素A不同水平下的样本均值与总平均值间的变异，用SA表示，叫做因素A的效应和；（2）在Ai水平下的样本均值与样本值xij之间的变异，用SE表示，它是由随机误差引起的，叫做误差平方和。SA和SE为

在上面两式中，fA、fE分别为SA和SE的自由度。则有

2）计算均方和及其F值。因素A和误差E的均方和为

3）选择合适的显著性水平α，对原假设进行检验 。 若 F＞Fα(fA,fE)，则 拒 绝 H0；反 之 ，若F＜Fα(fA,fE)则接受原假设。

2.3 参数估计

当检验结果为显著时，可以使用点估计和区间估计的方法对总均值、各水平均值和误差方差进行估计。这些参数的最大似然估计为

2.4 多重比较

如果方差分析的结果因子A显著，可以认为因子A的各水平效应不完全相同，此时，我们还需要进一步确认哪些水平均值间是有差异的，哪些水平间无显著性差异。

在r(r＞2)个水平均值中同时比较任意两个水平均值间有无明显差异的问题称为多重比较［11～12］。

常用的多重比较方法有最小显著极差法［11］、最小显著差数法（LSD）［11］、Tukey检验法［12］等方法。

3 单因素方差分析对雷达距离精度试验的结果分析

在某型雷达精度试验中，选用海拔高度作为试验变量，其他影响因素尽量保持一致。该变量共有a=3个试验水平，它们分别为10000m、100m和35m，雷达一次差数据相应地为x1,x2,x3，样本量均为n=44。现在使用方差分析技术来判断海拔高度这一变量是否对雷达跟踪精度产生显著性影响。三个水平下的雷达跟踪一次差图如图1所示。

3.1 试验数据的三个假定性判断

判断三个水平下的试验数据是否满足方差分析所要求的三个假定。

1）正态性检验

本文在这里采用夏皮洛-威尔克检验方法，该方法的检验统计量为

其中系数a1,…,an为在样本容量n时有特定的值，需要查阅相关表格，x(i)为待检验数据x的次序统计量。相应的拒绝域为

经过计算在三个试验水平下的W值分别如下：

三个W值大于在显著性水平α=0.05下的W0.05=0.944（n=44），可以认为在三种不同海拔高度下的雷达一次差数据服从与正态分布。

2）方差齐性检验

方差齐性检验方法，本文在这里采用Bartlett检验方法。该方法的检验统计量为

其中 fi、分别为r=i水平下的自由度和样本方差，其中C为

经过计算三种不同海拔高度下的样本的统计量B为2.9715，在α=0.05的显著性水平条件下，(3-1)=5.9915。说明三个水平下的样本满足-0.05方差齐性要求。

3）独立性检验

由于三个不同海拔高度下的雷达精度试验均是独立进行的，因此三个样本的数据可以保证为是互相独立的。

3.2 试验数据的方差分析

使用方差分析技术对试验数据进行分析，分析的结果如表1所示。

表1 单因素方差分析结果表

在 α=0.01的 显 著 性 条 件 下 ，F0.01(2,129)=4.77。F=357.20大于F0.01(2,129)，故拒绝原假设H0，接受H1。该结果说明目标海拔高度对雷达精度产生了显著性影响，需要进一步研究分析。

3.3 雷达精度参数估计

使用点估计和区间估计，对雷达精度试验的参数进行估计。令α=0.05，误差方差的无偏估计为σˆ2=MSE=0.28，各水平均值的1-α置信区间为

3.4 多重比较

本文在这里采用LSD法进行多重比较。LSD法被称为最小显著性差数法，是指两个处理的平均数差数达到显著的最小尺度，其计算公式为

当 ||μi-μj＞LSDα，则认为 μi与 μj间存在显著性差异，否则，无显著性差异。

LSD0.05=0.2212，LSD0.01=0.2923。使用梯形表将多重比较结果表示如表2。

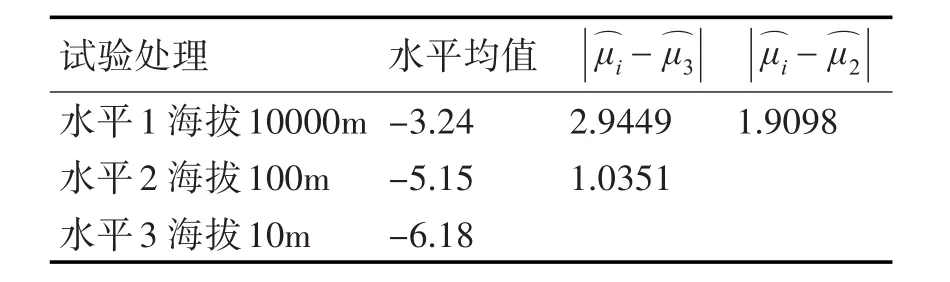
表2 多重比较结果表

4 结语

影响雷达距离精度的因素有很多，本文在这里主要针对目标海拔高度这一因素进行了分析。首先对试验数据是否满足方差分析的三个假定进行了判断；其次利用方差分析判断这一因素对距离精度是否产生显著性影响，在结果显著的基础上，对试验参数进行了点估计和区间估计；最后进行了多重比较分析，进一步地查明哪些试验水平均值间存在显著性的差异。

当然，方差分析方法可以用于其他多种因素对雷达精度的影响分析。分析得到的结果，对于研制方，可以修正已有设计的不足，改进设计和使用材料，对于使用方，明确知道性能不足的范围，在使用时进行规避，以发挥雷达的最大效能。