反舰导弹巡航高度决策研究∗

2018-11-26沈培志王培源

舰船电子工程 2018年11期

沈培志高健王培源

（海军航空大学烟台 264001）

1 引言

反舰导弹射程远、命中率高、杀伤威力大［1］，在现代海战中通常担负“首战首突”任务，是精确打击海上目标的杀手锏武器。反舰导弹射击诸元较多，诸元决策的准确性直接影响导弹命中概率，进而可能对作战全局造成影响。文献［2～11］对反舰导弹射击方式、雷达搜索图、导引头开机距离、开机高度、巡航高度等射击诸元进行了研究，其建立的雷达搜捕、终点散布、目标机动等模型，参考和借鉴价值较高。

反舰导弹射击诸元决策，指决策者在诸元规定取值范围内确定一个参数值，作为该诸元飞行弹道装订值。以往射击诸元研究中，理论性强，研究成果偏重于提供决策依据，而整个决策过程研究不全面，通常缺少决策值确定环节。

本文将以巡航高度诸元为对象，开展全过程决策研究，望能为指挥决策提供参考。

2 反舰导弹高度诸元决策一般原则

反舰导弹高度诸元包括巡航高度、第一次开机高度、第二次开机高度、超低空平飞高度、俯冲高度等诸元。根据导弹性能和作战要求，高度诸元决策通常考虑“不被发现”、“不被抗击”、“看得见”、“击得中”、“不击水”等原则。

1）“不被发现”，即导弹位此高度飞行，不会被目标探测设备探测到；

2）“不被抗击”，即导弹位此高度飞行，不会被目标舰空导弹攻击到；

3）“看得见”，即导弹位此高度飞行，导引头能够搜索到目标；

4）“击得中”，即导弹以此高度撞击目标，能够重伤甚至击沉目标；

5）“不击水”，即导弹位此高度飞行，不会撞到海水。

导弹飞行过程中，受不同阶段、不同高度、不同目的制约，上述原则不可能同时满足，必有取舍。

3 反舰导弹巡航高度决策原则

当今大部分反舰导弹已实现巡航高度可装订，且装订值只能为整数；导弹巡航高度诸元是导弹飞行自控段［12］诸元。因此，定义反舰导弹巡航高度诸元决策为，在导弹武器系统规定高度取值区间内确定一个整数值，作为导弹自控段掠海飞行高度。

根据武器性能和高度诸元决策一般原则，对反舰导弹巡航高度诸元决策遵循原则分析如下：

1）巡航高度位于导弹飞行自控段，而导弹采用自控段掠海飞行的目的即为降低被发现概率，因此巡航高度决策必须考虑“不被发现”原则；

2）导弹飞行自控段导引头不开机，且距目标尚有一段距离，因此不用考虑“看得见”和“击得中”原则；

3）根据武器作战使用要求，反舰导弹通常用于6级以下海况，由表1知，6级海况最大波高为8.5m，而目前绝大多数反舰导弹巡航高度在10m以上，因此可认为导弹位巡航高度飞行不受海浪影响，即不用考虑“不击水”原则；

4）根据舰空导弹反导机理，目标舰船在对来袭导弹进行抗击时，使用搜索雷达对空搜索，若未发现目标，则不抗击，因此对反舰导弹来讲，若“不被发现”，则肯定“不被抗击”，即若考虑“不被发现”原则，则不用考虑“不被抗击”原则。

综上，巡航高度诸元决策只需考虑“不被发现”原则。

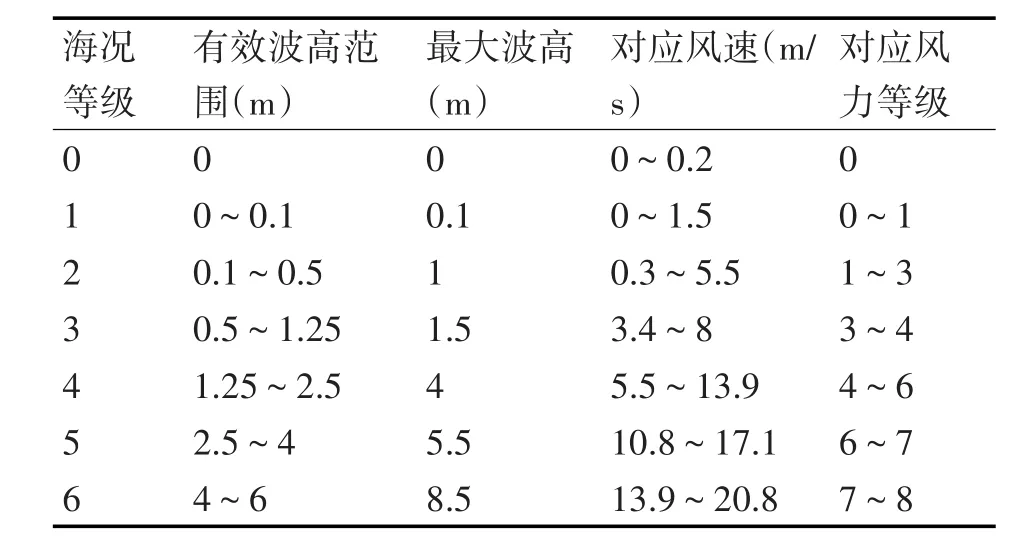
表1 海况与风力对应关系表

4 反舰导弹巡航高度决策模型

4.1 模型假设

基于以上分析并结合实际，模型建立前作如下假设：

1）目标仅用舰载雷达进行对空探测；

2）不考虑导弹隐身性和海杂波对雷达探测影响；

3）雷达探测距离受地球曲率影响。

4.2 数学描述

根据上述假设，绘制巡航高度诸元决策模型图，如图1所示。图1中，Hx为巡航高度，Hk为一次开机高度，hk为二次开机高度，Hc为超低空平飞高度，Hf为俯冲高度，Hm为目标舰载雷达天线高度，Rkj为一次开机距离，rkj为二次开机距离；A为导引头一次开机爬升点，对应海平面映射点K；B为一次开机点，海平面映射点L；C为一次开机高度向二次开机高度降高点，D为二次开机高度巡航起始点；E为二次开机点，海平面映射点M；F为二次开机高度向超低空平飞高度降高点，海平面映射点N；G为超低空平飞起始点；H为超低空平飞高度向俯冲高度降高点，海平面映射点O；I为俯冲高度飞行起始点；J为目标舰载雷达。

根据武器性能，导弹通常于第一次开机前Δr时开始向一次开机高度爬升。由图1知，只要目标舰载雷达对巡航高度Hx最大探测距离Dx不超过A点，则反舰导弹“不被发现”，数学描述：

上式，距离单位为km。

4.3 模型解算

受地球曲率限制，目标舰载雷达对巡航高度Hx最大探测距离Dx与自身天线高度Hm、反舰导弹巡航高度 Hx有关，其表达式［11］：

式中，Hx、Hm单位为m，Dx单位为km。

将式（2）带入式（1），整理得：

实际作战中在进行高度诸元决策时，通常经分析研判可得到一个决策依据表达式，如式（3），此式可能缩小诸元参数取值范围，但不能得到一个确定的决策值。高度诸元决策时，若高度取值过高则易被敌发现，过低则击水概率会增加，因此为方便决策，现提出一种保守的决策理论，简称中间值决策，此理论适用于巡航高度、第一次开机高度、第二次开机高度、超低空平飞高度、俯冲高度等诸元决策。

中间值决策：假设H表示需决策诸元，系统规定参数可装订范围为［a，b］，通过分析研判得决策依据表达式为H＜h1或H＞h2，则H决策如下：

5 反舰导弹巡航高度决策舍弃模型

5.1 模型假设

1）地球为正球形；

2）舰载雷达探测不受外界因素干扰，最大探测距离为其直线距离。

5.2 数学描述

图2中，O点为地球球心，Rd为地球半径，JS相切于海平面，其线段长度为舰载雷达对巡航高度Hx的最大探测距离，其他字母含义与图1相同。

设线段JS对应球心夹角为φ1，巡航段末端与目标舰船的海平面映射点连线KR对应球心夹角为φ2，则“不被发现”的数学描述：

上式，角度单位为弧度。

5.3 模型解算

根据几何关系可知：

因JS相切于海平面，由三角函数得

根据武器性能，导弹于第一次开机前Δr开始爬升，因此弧线KR长度为Rkj+Δr，则

将式（10）、（11）带入式（7）即可求得巡航高度Hx决策依据表达式。

5.4 模型说明

上述模型虽然可以解算，但实际上地球并不是正球形，地球半径Rd约6371km，而目标舰载雷达高度和巡航高度均在百米以下，与地球半径相比几乎可忽略不计，若模型中Rkj、Δr、Hm稍有变化，解算结果中巡航高度Hx变化将很大，难以决策。因此，研究决定放弃此模型，但为避免他人在类似研究中走弯路，故作以上说明。