静子叶片表面状态对涡轮性能影响的研究

王晓锋，毛 凯，许开富，李向阳，王 琳

(1.西安航天动力研究所，陕西 西安 710100; 2.西安航天发动机厂，陕西 西安 710100)

0 引言

在采用富氧燃气发生器循环的高压补燃循环液氧煤油发动机中，主涡轮的效率和流通面积是进行系统调整计算的重要参数，其偏差直接影响发动机推力调节的准确性。随着研制任务的进展，我国某型液氧煤油发动机主涡轮静子的制造工艺发生了变化。熔模铸造生产的涡轮静子，其蜡模成型工艺由激光快速成型改为金属模具压制后，静子叶片表面状态有明显变化。因此研究叶片表面状态对涡轮性能的影响，对于控制生产质量、改善发动机系统调整计算精度具有重要的工程价值。

以叶轮为工作部件的旋转机械，由于制造和使用工况等因素造成叶片表面粗糙度变化后，会影响边界层分布和流体绕流状态，进而影响叶轮机械的性能。对叶片表面粗糙度的研究主要有整体粗糙度和局部粗糙度两个方面。整体粗糙度增加会降低叶轮机械性能，并且粗糙度越大，性能损失越严重[1-2]。而叶片局部粗糙度增加带来的影响则有所不同，合理增大粗糙度以及调整其位置分布可以更好地抑制分离、减小叶型损失[3-4]。

本文所述涡轮静子叶片表面状态的变化严格讲是叶型发生了变化，但又与表面粗糙度类似，因此参考粗糙度的概念进行对比分析。本文针对激光快速成型工艺特点，利用均匀划分的B样条曲线实现涡轮静子叶片不同表面状态的准确模拟，并通过数值计算方法分析其对涡轮性能的影响。

1 静子叶片表面形状构造

不同工艺的叶片表面状态如图1所示。涡轮静子铸造用蜡模采用快速成型技术(RP：Rapid Prototyping)制备，由于其分层扫描，逐层堆积的工作原理，蜡模表面明显存在分层扫描时形成的台阶[5-6]。在最终产品上则表现为叶片表面尤其是吸力面有明显的台阶。而利用金属压型模具制备的蜡模表面光洁度很高，实际产品表面粗糙度为6.3 μm。参考粗糙度的概念来衡量，快速成型产品表面粗糙度高达50 μm。快速成型静子最突出的特征是叶片表面的波浪状“台阶”，其台阶方向由蜡模的烧结方向决定，而激光扫描间距以及叶片表面曲率决定了台阶数量及高度。实际生产中后续工艺对台阶进行了适当的圆滑。

图1 涡轮静子叶片表面状态Fig.1 Surface state of turbine stator blades

为了便于利用数值仿真分析方法，本文利用MATLAB中spcrv函数生成的均匀划分B样条曲线来对叶片表面波浪状“台阶”进行模拟。如图2所示，利用间隔x模拟激光扫描间距，控制叶片表面“台阶”数目；通过调整B样条阶次控制叶片表面“台阶”高度y及圆滑程度。本文选择了4个阶次(10，20，30，40)的B样条曲线对叶片型线进行拟合，当x=0.25 mm时、吸力面B样条阶次为10，压力面B样条阶次为40时，静叶三维模型与实际产品状态基本一致，如图3所示。B样条阶次越高，拟合曲线与理论型线越接近，其偏差如图4所示，对应的最大偏差分别为54 μm，25 μm，12 μm，7 μm，基本涵盖了快速成型与金属压型产品的表面状态。从吸力面拟合情况也可以明显看出，相对于成型方向当叶片型线斜率越小时拟合偏差越小。

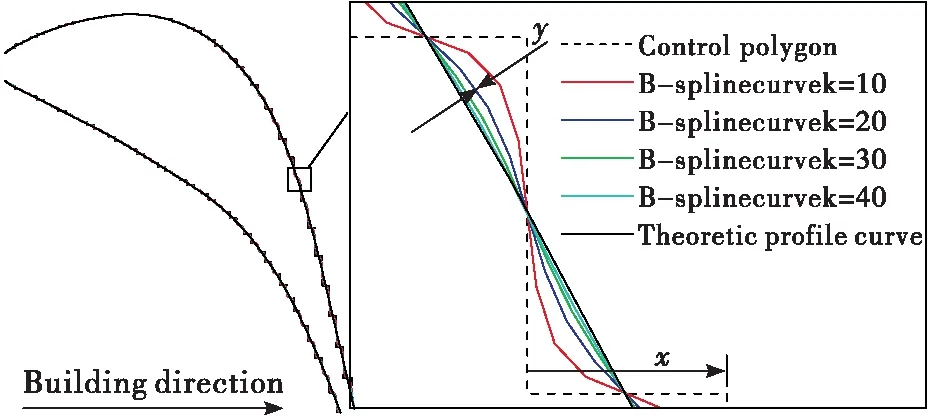
图2 样条曲线模拟叶片表面形状Fig.2 Spline curve fitting to surface shape

图3 静子三维模型Fig.3 3D model of turbine stators

2 数值分析方法与模型

流场仿真计算采用NUMECA Fine/Turbo软件进行，湍流模型为Spalart-Allmaras模型；转静子交界面采用全非匹配的混合平面方法，计算中采用了强化隐式加速收敛技术。实际涡轮工质为高温富氧燃气，由于氧的含量非常高，计算时工质按纯氧气考虑。进口给定总温总压，出口给定平均静压，固体壁面假设绝热并设定相应的转速[7]。

计算区域包括单个静叶和动叶通道以及动叶顶部泄漏通道，多块结构化网格如图5所示。其中静叶通道展向网格节点数为57，进口周向网格节点数为65，出口周向网格节点数为225；动叶通道展向网格节点数为57，进口周向网格节点数为85，出口周向网格节点数为89；通过增大叶片表面流线方向的网格节点数目(吸力面413，压力面213)以及调整节点分布来准确模拟叶片表面的波浪状“台阶”。

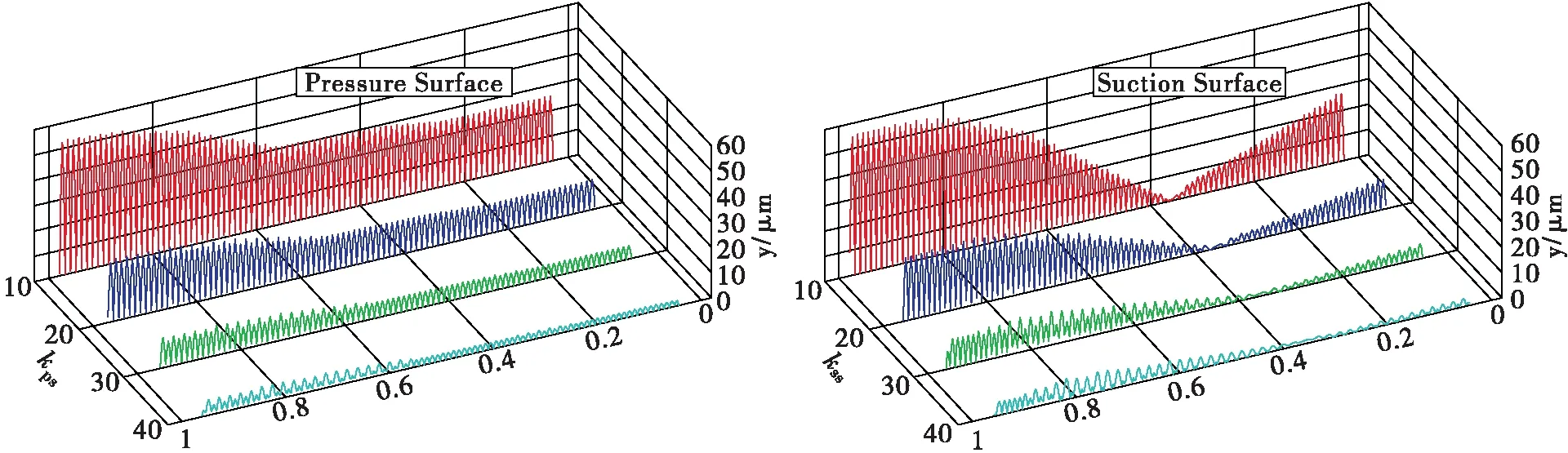
图4 曲线拟合偏差Fig.4 Deviation of curve fitting

图5 计算网格Fig.5 Computational grids

3 计算结果与分析

3.1 涡轮总体性能

除原始设计的理论模型外，根据上述方法，对静子吸力面、压力面分别用4种阶次的B样条曲线模拟，又构造了16种静子进行仿真分析。对其中5种模型进行了全工况的计算，其中模型B与产品实物状态基本一致，模型E为理论模型。在额定压比条件下，涡轮效率拟合曲线见图6(图6中数值依据理论型面计算结果进行了归一化处理)。在整个速比范围内，叶片表面越光滑，涡轮效率越高，额定点效率偏差最大；偏离额定点越多，效率偏差越小。对于压力面与吸力面均较光滑的模型D，其性能与理论模型非常接近，偏差仅为1%。

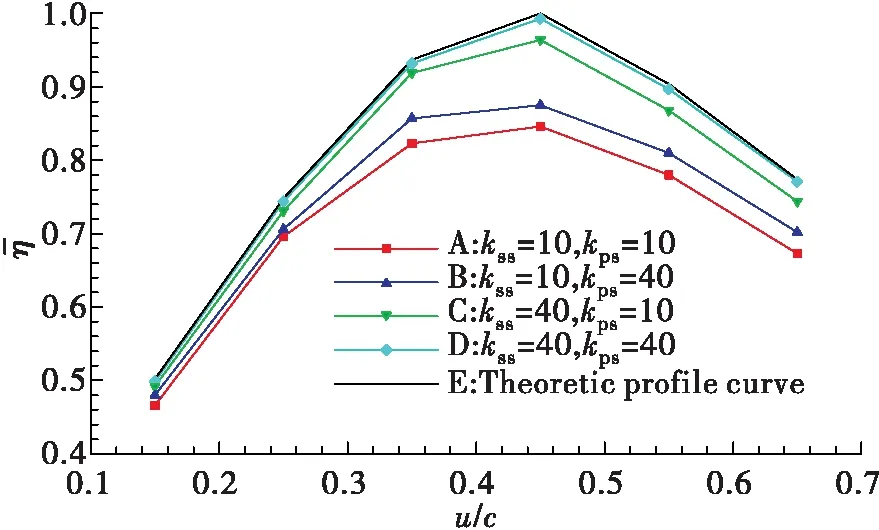
图6 涡轮效率曲线Fig.6 Curves of turbine efficiency

设计点涡轮效率和流通面积随叶片表面状态的变化如图7所示。其中涡轮效率为总静多变效率；由于静叶出口为超音速流动，流通面积根据流量及进口总温总压计算而得。从图7中可见，随着叶片表面光滑程度的增加，涡轮性能明显提高。静叶吸力面光滑程度对涡轮性能的影响比压力面更为显著，随吸力面光滑程度的增加涡轮效率和流通面积分别增大12%和3%；随压力面光滑程度的增加涡轮效率和流通面积分别增大3%和2%；压力面与吸力面均较光滑时，涡轮性能与理论模型性能非常接近，偏差仅为1%。

3.2 静叶总压损失

图8为静叶周向平均总压损失系数沿轴向的分布。可以看出，随着流体从静叶前缘处向后发展，总压损失逐步增加。对模型E来说，从静叶进口直到80%轴向弦长处损失均较小，随着流体流过喉部截面，损失急剧增加，最终在静叶出口达到最大值。模型C和D的损失大小与发展情况与模型E类似。而模型A和B具有相同的发展规律，但总压损失从60%轴向弦长处即开始急剧增大。由于此涡轮静叶展弦比仅为0.56，属于极小展弦比叶栅。叶片表面台阶加剧了上下端壁的低能流体向中部的扩展，使吸力面附面层增厚，导致损失急剧增加。叶片吸力面不光滑会导致总压损失明显增大，而且其影响范围更大，压力面台阶的影响则稍小。

图9为静叶出口截面(约108%轴向弦长)处周向平均总压损失系数沿叶高的分布。可见，对于模型A，出口低能流体占据叶片展向范围较大，在叶片中部以上和以下存在两个主要的低能区。提高叶片压力面光滑程度后(B)，叶片中部以下区域总压损失改善明显；提高叶片吸力面光滑程度后(C)，叶片中部以上区域总压损失得到明显改善；当吸力面压力面均比较光滑时(D)，总压损失分布与理想模型E非常接近，整个叶展方向没有大的低能区。

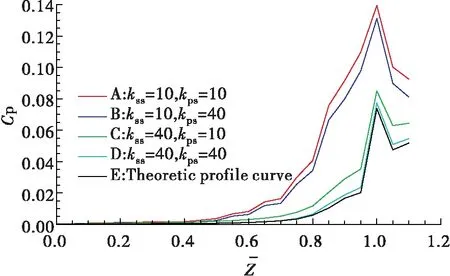
图8 静叶总压损失系数沿轴向分布Fig.8 Total pressure loss distribution along axial direction of stator blade

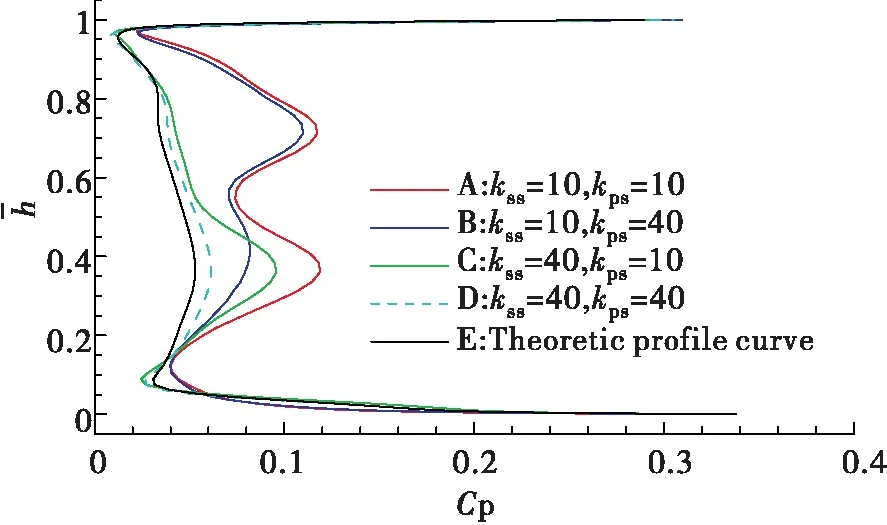
图9 静叶出口总压损失系数分布Fig.9 Total pressure loss distribution along spanwise at stator blade exit

3.3 静叶出口气流角

图10为静叶出口截面(约108%轴向弦长)处周向平均气流角沿叶高的分布。可以看出，对于理论模型E，叶展中部气流存在轻微的过偏转(静叶出口几何气流角为气流与周向夹角，设计值为12.5°。小于静叶出口几何角为过偏转；大于静叶出口几何角为欠偏转)，并逐渐过渡至两侧端壁处的欠偏转。模型D气流角分布规律几乎与理论模型重合。对于模型C，气流角在叶展中部基本不变，过偏转的区域稍有增大。叶高中部位置的气流轻微过偏转是由于压力面与吸力面压差造成横向流动而导致的；而在靠近两侧端壁区域由于一部分主流被通道涡卷吸而产生由吸力面向压力面流动的速度分量，因此存在一定程度的欠偏转。对于叶片吸力面不光滑的模型A和B，叶展中部至叶根端壁有轻微过偏转，叶展中部至顶部端壁区域的气流欠偏转区域更大、过渡更快，从图11所示的80%叶高截面的马赫数云图可以明显看出，这主要是由于吸力面低能流体积聚对主流排挤所造成的。

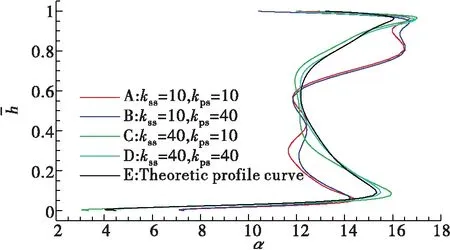
图10 静叶出口周向平均气流角Fig.10 Averaged flow angle distribution along circumference at stator blade exit

从上述分析可以看出，由于金属压型静子叶片表面更加光滑，明显改善了静叶的性能。同时静叶出口气流参数的变化又使得动叶进口条件更接近设计工况，最终导致涡轮总体性能明显提高。

4 结论

利用均匀B样条曲线，通过调整控制点间隔和样条阶次，可以实现涡轮静子叶片表面波浪状“台阶”的准确模拟。

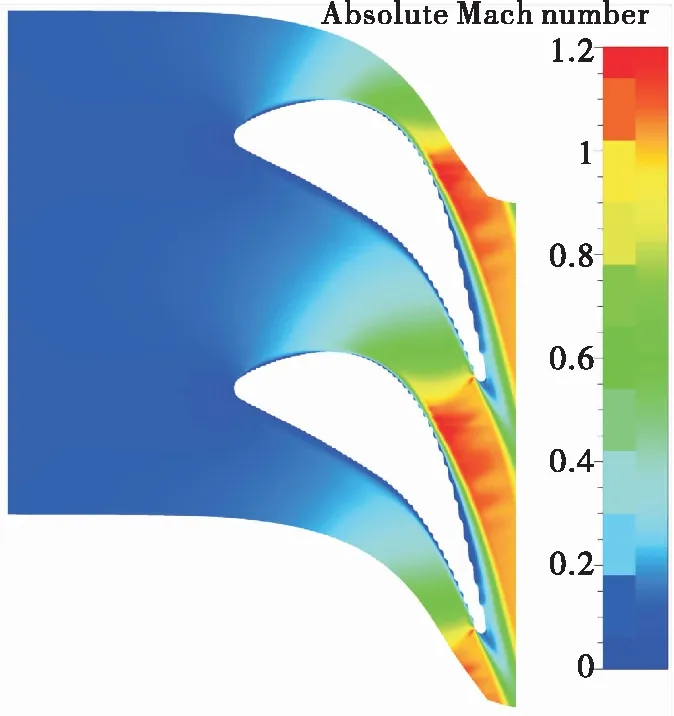
图11 模型A 80%叶高截面马赫数分布Fig.11 Mach number distribution at 80% span section of model A

静子叶片表面状态对涡轮内部流动有明显的影响，表面越光滑涡轮性能越接近设计值。叶片吸力面偏差对性能的影响要大于压力面的影响。

静子叶片表面偏差达到7 μm时，涡轮性能与设计值偏差仅为1%，完全满足发动机系统调整计算的精度要求。