齿轮箱圆锥过盈连接计算及拆装方法

常 星， 宋俊龙

（智道铁路设备有限公司， 山西 太原 030032）

齿轮箱是机车产品关键技术之一。由于过盈连接结构简单，定心精度高，可承受转矩、轴向力或两者复合的载荷，对轴削弱小，承载能力高，并且在冲击、振动载荷下也能可靠地工作。因此，在齿轮箱设计过程中，大量的选用过盈连接来传递载荷。

圆锥过盈连接相较圆柱过盈连接而言，包容件和被包容件无需进行冷却或加热，采用油压法就能进行装拆。设备简单，操作安全、灵活。同时由于高压油膜的存在，在压装和拆卸的过程中可以对圆锥表面形成保护，降低配合表面的摩擦系数，从而降低擦伤结合表面的概率。尤其是当传递载荷大、过盈量大，并且定期需要装拆、检查、维修零部件的时候，可以大大降低由于频繁拆解造成损伤需要更换零部件的频率，进而节约成本[1]。并且由于机车产品的特殊性，对产品安全性、可靠性等有严格的规定。在产品的生命周期内，按照规范需要定期拆装、监控、检查关键零部件的性能状态。因此，在过盈连接的设计计算中，通常优先选用圆锥过盈连接。

1 圆锥过盈连接的设计计算

在具体设计圆锥过盈连接时，根据实际使用工况和约束条件确定相关零部件基本结构尺寸后，首先是根据具体传递载荷的大小以及材料的特性选择合适的圆锥过盈配合，其次是计算过盈连接的装拆参数，最后需要综合考虑结构并确定合理的装拆方法。

1.1 圆锥过盈配合的计算[1,2]

1.11传递负荷所需最小过盈量

1）传递负荷所需的最小结合压力。

式中：M 为传递扭矩，N·mm；K 为安全系数；lf为接合长度，mm；μ为摩擦系数；dm为结合面平均圆锥直径，mm。

2）包容件直径比。

式中：da为包容件外径，mm。

3）被包容件直径比。

式中：di为被包容件内径，mm。

4）包容件传递负荷所需的最小直径变化量。

式中：Ca和Ea为计算系数，查阅参考文献[1]相关表格获得。

5）被包容件传递负荷所需的最小直径变化量。

式中：Ci和Ei为计算系数，查阅参考文献[1]相关表格获得。

6）传递负荷所需的最小过盈量。

考虑压平量的最小过盈量。

式中：Raa为包容件轮廓算术平均偏差；Rai为被包容件的轮廓算术平均偏差。

1.1.1 不产生塑性变形所容许的最大有效过盈量

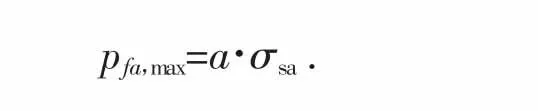
式中为包容件材料屈服点，MPa。

2）被包容件不产生塑性变形所容许的最大结合压力。

3）连接件不产生塑性变形的最大结合压力。

4）包容件不产生塑性变形所容许的最大直径变化量。

5）被包容件不产生塑性变形所容许的最大直径变化量。

6）连接件不产生塑性变形所容许的最大有效过盈量。

1.1.3 选择配合

选出的配合，其最大过盈量[δmax]和最小过盈量[δmin]应满足下列要求。

1）保证过盈连接传递给定的负荷。

2）保证连接件不产生塑性变形。

初选基本过盈量δb，按初选的基本过盈量δb，最大圆锥直径，δe，max、δmin，参照 GB/T 5371、GB/T 1801 和GB/T 1802，确定选用的配合。

给出配合的最大过盈量[δmax]和最小过盈量[δmin]。

1.2 油压装拆相关参数的确定

在装拆圆锥过盈连接的过程中，主要是使用油压法进行装拆。即在包容件和被包容件之间的结合面上，注入符合压力要求的高压油，使包容件和被包容件之间的结合面发生弹性变形，形成间隙，同时在结合面之间形成一道油膜。

安装时，需要使用特定的液压装置，在被包容件上施加不小于特定值的轴向推力，将被包容件推入包容件内。而拆卸时，当高压油在带有锥度的结合面上形成的轴向分力足够大时，被包容件会自动从包容件中退出。

1.2.1 轴向位移极根值和轴向位移公差的计算

如图1和图2所示，由于内、外圆锥直径公差带的原因，实际初始位置应位于极限初始位置1和极限初始位置2之间，即内圆锥为最小极限圆锥、外圆锥为最大极限圆锥和内圆锥为最大极限圆锥、外圆锥为最小极限圆锥之间。终止位置是为了使内、外圆锥得到要求的过盈量，所规定的相互轴向位置。而轴向位移极限值即是为了得到最小过盈量和最大过盈量的轴向位移量[3]。

图1 最大、最小过盈位置示意图

图2 初始位置变动量示意图

由于通过控制圆锥配合相对轴向位移量，可以实现精确调整其过盈量。因此，在生产实践中，这是评估相互配合圆锥表面加工精度以及实际过盈量是否满足要求的重要指标，尤其是圆锥配合需要频繁拆卸、安装的场合。当拆卸后零件尺寸检验或相关零件重新装配时，特别是材料硬度较差的情况，都必须通过测量起始位置和终止位置的数据，来间接评估轴向位移公差是否能满足实际使用要求，一定程度上可以实现间接检测内、外圆锥是否超差。

1）轴向位移极限值。

式中：C为结合面锥度。

2）轴向位移公差。

1.2.2 装拆油压入力的确定

除上述参数以外，还需要确定合理的装拆油压，进而选择合适的高压油泵。并且安装时，也需要使用满足压入力要求的液压推力装置将圆锥过盈配合压装到位。

1）配合面最大结合压力。

2）装拆油压。

3）压入力。

实际操作中，除了油压法，有时也会用到胀缩法对圆锥过盈配合进行装拆。尤其是特殊情况下，使用油压法在合理压力范围内无法拆卸成功时，需要结合胀缩法和油压法进行拆卸，即加热包容件至一定温度，然后打入高压油完成拆卸。而装配过程使用胀缩法，如果能够合理计算安排生产节拍，将省去油压法装配的保压时间，进而可以大大提高生产效率。

但需要注意加热包容件时，加热应均匀，不得产生局部过热。通常可以采用加热炉或电磁感应加热装置。未经热处理的装配件，加热温度应小于400℃，经过热处理的装配件，加热温度应小于回火温度。

1.2.3 典型装拆方法

图3为圆锥面过盈配合装配原理示意图。通过油杆1中心的油孔向圆锥配合表面注入满足装拆油压要求的液压油，同时油杆1穿过液压推力装置2的中心，并通过螺母3将液压推力装置轴向进行限位。装配时，首先是注入高压液压油，当圆锥配合表面有油液渗出时，开始操作液压装置，将外圆锥件推入内圆锥件中[4]。

图3 圆锥面过盈配合装配原理示意图

图4为圆锥面过盈配合拆卸原理示意图，与装配过程不同的是，此处不需要液压推力装置。由于圆锥过盈配合的特性，当注入一定压力范围的液压油后，待其配合面充分润滑后，内圆锥件和外圆锥件会自动脱离，并且速度快、冲击力大。因此需要在中间合适距离位置安装缓冲装置2，用来吸收冲击力，并避免装配件磕碰损伤。

图4 圆锥面过盈配合拆卸原理示意图

实际生产中，特别需要注意的是，上述高压元件长期处于高压、变载荷、高冲击的工作环境中，为了生产安全，需要定期检查、更换各相关元件。

2 设计实例

以某机车产品齿轮箱输入端连接为例，其输入轴与联轴器为圆锥过盈连接，锥度1∶50，传递扭矩M为824 N·m，结合面平均圆锥直径dm为67.08 mm，结合长度lf为88 mm，材料为17Cr2Ni2Mo，屈服强度σs为1 050 MPa，表面粗糙度Ra为0.8。

按照上述计算方法，传递负荷所需的最小结合压力pf，min=22 MPa，包容件传递负荷所需的最小直径变化量ea，min=0.020 1 mm，被包容件传递负荷所需的最小直径变化量ei，min=0.015 9 mm，传递负荷所需的最小过盈量δe，min=0.036 mm，考虑压平量的最小过盈量δmin=0.041 mm。

包容件不产生塑性变形所容许的最大结合压力pfa，max=323.4 MPa，被包容件不产生塑性变形所容许的最大结合压力pfi，max=525 MPa，连接件不产生塑性变形的最大结合压力为pf，max=294 MPa。包容件不产生塑性变形所容许的最大直径变化量ea，max=0.269mm，被包容件不产生塑性变形所容许的最大直径变化量ei，max=0.212 mm，连接件不产生塑性变形所容许的最大有效过盈量 δe，max=0.481 mm。

然后，初选基本过盈量δb=0.261 mm，配合尺寸为 H7/z6，最小过盈量[δmin]=0.18 mm，最大过盈量[δmax]=0.229 mm。

轴向位移极限值 Ea，min=9 mm，Ea，max=11.45 mm，轴向位移公差TE=2.45 mm，配合面最大结合压力[pf，max]=139.9 MPa，装拆油压 px=153.9 MPa，压入力Pxi=85 578.6 N。

根据上述计算结果，内锥选取H7，外锥选取z6，并且装配时应确保压入行程在9mm至11.45mm之间。高压油泵应至少满足153.9 MPa压力范围，选取的液压推力装置应满足压入力不小于85 578.6 N的要求。

3 结论

由于机车产品的特殊性，其齿轮箱输入和输出部分传递扭矩经常采用圆锥过盈配合。本文详细介绍了圆锥过盈配合的计算过程，以及常用装拆方法油压法的相关参数及典型结构。

实际生产中，当重新使用拆卸后的零件之前，应仔细检查是否有影响使用的缺陷，特别是内、外圆锥面，拆卸后尺寸会有细微的变化，原则上应重新对传递载荷复核计算。

此外，经过频繁拆装的圆锥过盈配合，由于表面压平的原因，使得过盈量相对有所减少，相比上述计算值，应考虑适量增大轴向位移极限值0.5～1.0mm。而当环境温度低，液压油黏度变大，此时可以适当增大装拆油压以提高效率，但一定不允许超过引起材料塑性变形的极限值。