学习处处有算法

渠慎情

教材中的流程框图与伪代码都是算法的外在体现形式，而算法的本质就是对一类问题的机械的、统一的求解方法.在我们的高中数学必修一与必修二教材里，处处闪耀着算法思想的光辉，

函数解题循套路

函数的学习是高中数学的重中之重.会学，妙不可言；不会学，玄之又玄.其实，学习函数也有机械的、统一的学法.

我曾这样说过：函数的定义域、值域、单调性、奇偶性及周期性像朵朵花儿，静静地生长在函数这条枝蔓上，因此，要想学好函数，就要一一学好函数的定义域、值域、单调性、奇偶性及周期性.各个击破，融会贯通，你的函数也就学好了.

下面找些与函数有关，且很有算法风格的问题与大家共同探讨.

一、证函数单调性

证明或是判断函数在某个区间上的单调性时，大家常会看到一个个很好的套路或步骤，如“一取二比三定论”：取值，作差（商），比较，下结论（或设量，作差（商），判号，比较，下结论）.虽然，学无定法，但是证明函数是否单调的机械性与统一性在这里还是体现得淋漓尽致，当然，上面的任何一个具体的套路，都能很好地解决函数的单调性问题，

可以用流程图来表达上面的某些步骤，如图1所示：

二、判函数奇偶性

判断函数的奇偶性，也是有章可循的。

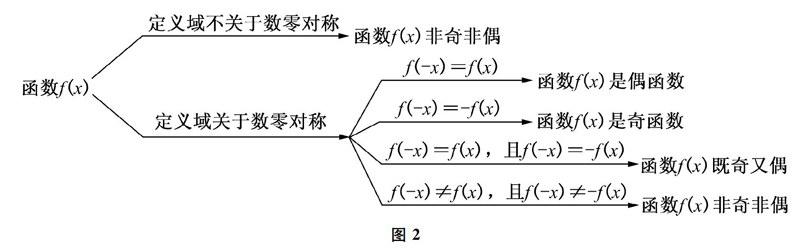
一般地，先求定义域，再判断定义域是否关于数零对称，若不对称，则函数非奇非偶，否则继续判断函数f（-x）与f（x）是相等还是相反关系.

若f（-x）与f（x）是相等关系，则函数f（x）是偶函数；若f（-x）与f（x）是相反关系，则函数f（x）是奇函数；若.f（-x）与f（x）既相等又相反，则函数f （x）既是奇函数又是偶函数；若f（-x）与f（x）既不相等也不相反，则函数f（x）既不是奇函数也不是偶函数，如图2所示：

三、定函数零点区间

在判定图象不间断的函数的某一零点是否在某区间内时，结合二分法，找寻零点所在区间的过程显得十分机械化.

一般地，要先结合函数图象，定下函数某一零点大致所在区间（a，b）（在此区间上有唯一零点），即对端点a与b求函数值f（a）与f（b），判断f（a）.f（b）的正负.若负，则零点在该区间内；若正，则不符合我们的要求，找到符合要求的区间（a，6）后，结合区间中点二分该区间，得区间（a，a+b/2）与（a+b/2，b），然后对这两个区间继续求端点值，判断端点值乘积的正负，依此类推……

除了函数到处体现着算法的思想，立体几何、解析几何中算法的思想也是无处不在，

“立几”、“解几”有算法

高中立体几何（有时简称“立几”）的问题中，证明线面平行与线面垂直是最常见的.而这里也有机械统一的解决问题的思想方法.

一、环环相扣论线面

如图3，看看证明线面平行的一般步骤：先找线线平行，再说明一条直线在面内，一条直线在面外.如此三步，线面平行证得，

如图4，再看看线面垂直：证线线垂直，再证线线垂直，弄清线线相交，最后说明两线在面内.此乃证明线面垂直之五步.

四个公理、三个推论、八个定理构建起高中立体几何证明的依据平台，再加上一定的逻辑表达，即可证明直线与平面之间的平行和垂直关系.

立体几何如此，解析几何（有时简称“解几”）亦如此.

二、步步严谨求切线

在直线与圆的位置关系中还是有些值得探讨的问题，下面就来看看在直线与圆之间有何问题能机械统一地求解，

若已知点的坐标，如何求过该已知点的圆的切线方程呢？

第一步要做什么呢？设切线的斜率吗？不是！

第一步是要判断已知点与圆的位置关系，即点在圆外，圆内，还是圆上.这样，如果点在圆外，则必有两条切线；如果点在圆上，则仅有一条切线；如果点在圆内，则过点的直线必与圆相交，绝不相切.若点在圆外，且仅求得一条切线的方程，则要看看你是否少了一条斜率不存在的切线，

第二步，又要怎么做呢？设切线的斜率吗？还不是！

看切線的斜率是否存在，结合图形，若斜率不存在满足与圆相切，则得一切线；若切线的斜率都存在，则可执行第三步，

第三步，设切线的斜率为k，根据直线与圆的相切的关系，由“圆心到直线的距离d等于圆的半径r”构造关于参数k的方程，继而解之，得k.

第四步，由已知点与所求k确定直线的方程，

简言之，判定点与圆的位置关系，确定切线斜率存在与否，设直线斜率并求之，最后得方程.如图5所示：

依据上面四步，可求圆的切线方程.此法可机械且统一地解决如此一类问题，算法思想便再次得以体现，当然，算法并不唯一，上面的四步自然也不是求圆切线方程的唯一方法.

三、点点明确定未知

曾无数次在课堂上向学生们夸下海口——只要给我三角形的三个顶点的坐标，你让我求啥，我就能求啥！其实，只要掌握了解决问题的关键方案，你也能轻松解决问题，

学生们最喜欢问的一个问题是：已知三角形的三个顶点的坐标，如何求它的内切圆方程.

我们分析一下：

求内切圆的方程，就是求圆的方程；要求圆的方程，就要求该圆圆心坐标与半径大小；求三角形内切圆的圆心，就是求该三角形的内心，即角平分线的交点；要求角平分线的交点，要先求角平分线的方程，而求角平分线的方程才是大家认为内切圆难求的主要原因，

如何求角平分线的方程呢？

有一种方法是这样的：设角平分线上任意一点的坐标为（x，y），则该点到相应两边的距离相等，根据该条件构造关系式，简化关系式后得到的方程就是角平分线的方程，简言之，设点，构造方程，化简.

如此，再求另一条角平分线的方程，继而求两角平分线的交点，即为三角形的内心，也就是该三角形内切圆的圆心，

如何求半径呢？圆心到任意一边的距离就是圆的半径.那么，边所在直线的方程怎么求呢？呵呵，你懂的，

上面说得看似有点复杂，画个简单的流程图就容易看懂：

算法，未必是一个框图、一个伪代码.有时，它更是一种思想.按部就班的套路.机械统一的解决问题的方案，就是算法.无论是函数，还是立体几何，解析几何，探索数学未知的路还很长.借助算法的原则性，您可以不断地总结出一些有用的经验，再加上您思维的灵活性，以不变应万变，也许，您在这条学习数学的路上能走得更顺一些！