基于MATLAB的永磁同步电机位置观测器设计与仿真
2018-11-22安徽理工大学高子彦
安徽理工大学 高子彦
国网铜陵市义安区供电公司 张 陈
本文基于滑模变结构理论设计了永磁同步电机位置观测器,通过引入双锁相环(PLL)进行位置信号的解算,使波形更平滑,并在MATLAB软件中进行了仿真。仿真结果表明,该观测器能够实时正确辨识电机位置和速度。
引言:永磁同步电机(PMSM)以其简单,高效的特点,被广泛应用于工业伺服驱动、电动汽车等领域。精准的转子位置信息对于高性能PMSM牵引系统至关重要。 一般地,其位置信息通过硬件传感器获得,但是安装传感器会增加系统成本和安装尺寸,而且面对复杂的环境,硬件传感器的可靠性会受到挑战。故无传感器PMSM控制技术的研究逐渐变成一个热点。
PMSM基于无传感器控制的研究方向主要有低速和中高速两个方向。前者,通常采用高频信号注入法。 后者,控制技术主要有:扩展卡尔曼滤波法(EKF)、模型参考自适应法(MARS)及滑模变结构法。EKF需要计算能力强大的控制器,且难以确定卡尔曼增益;MARS需要电机精确的数学模型,且计算精度易受电机参数变化的影响。相比较而言,滑模控制具有不连续性,对外部干扰和参数变化不敏感,具有较强的鲁棒性和抗干扰能力。因此,在电机控制领域具有广泛应用前景(谷善茂,何凤有,谭国俊,等.永磁同步电动机无传感器控制技术现状与发展[J].电工技术学报,2009,24(11):14-20)。
本文在 MATLAB中搭建 PMSM控制系统仿真框图,并按照PMSM数学模型,设计滑模观测器。在滑模观测器的定子反电势输出端,利用双锁相环方法提取转子位置角与转速(姜建国,韩康.基于滑模观测器的PMSM无位置传感器矢量控制[J].组合机床与自动化加工技术,2017(7):126-129)。最后基于MATLAB仿真验证该观测器的有效性。
1 PMSM的数学模型
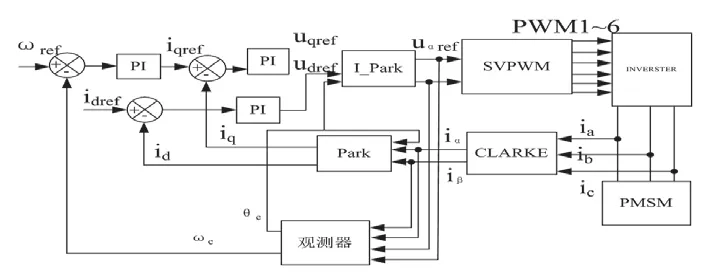
图1 PMSM的无传感器矢量控制框图

图2 基于双PLL滑模观测器SIMULINK仿真模型
PMSM一般采用的矢量控制,控制系统如图1所示。在静止两相α-β坐标系下,PMSM的数学模型表达式为:
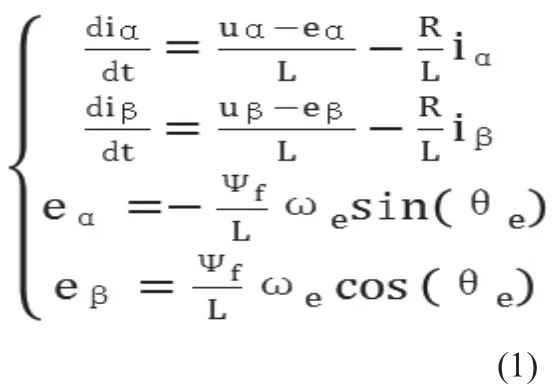
式中,R为定子电阻;对于表面式PMSM,定子电感Ld=Lq=L;iα,iβ,uα,uβ,eα,eβ分别为α—β坐标系下定子电流,电压和反电动势;ψf为转子永磁磁链;θe,ωe分别为转子位置角和转速。
2 滑模观测器的设计与仿真

式中,和是电流误差的开关信号,其中包含反电动势的信息。
首先,根据式(2)的数学模型搭建滑模仿真,为了减弱滑模抖动,采用饱和函数代替符号函数sign(姜建国,韩康.基于滑模观测器的PMSM无位置传感器矢量控制[J].组合机床与自动化加工技术,2017(7):126-129)。然后搭建PLL仿真模块,提取定子反电势,中的转子位置和速度信息(贺建军,段勇,喻寿益.基于滑模观测器的SPMSM位置速度估计[J].控制工程,2012,19(3):527-530;杨立永,谢晓峰,陈智刚.基于反电动势PLL法的PMSM无传感器控制研究[J].电力电子技术,2016(12):88-90)。为了使解算的电机位置信号更加平滑,再次加入一个PLL位置估算模块,以削弱高次谐波。滑模观测器的MATLAB仿真模型如图2所示。
3 仿真结果分析
本文在MATLAB/SIMULINK中对设计进行了仿真,验证了设计方案的观测效果。机参数如下:VDC=300V,定子电阻R=2.875Ω,电感L=0.00835Mh,极对数P=4,给定速度900rpm;外部负载TL=20N·m。根据仿真效果波形图3和图4所示,可知该仿真模型能够平滑解算 转子实时位置,具有一定实用价值。
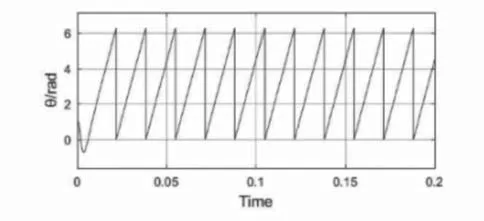
图3 电机位置解算

图4 转速误差波形
