梯度提升树在月售电量预测中的应用

四川中电启明星信息技术有限公司 李欢欢 王紫鹏 倪平波 张 强

新电改背景下，对售电量进行精准预测，不仅有利于规避电力交易中心的偏差考核，更能提升竞争性售电公司的核心能力、促进公司良好运营。本文在此背景下研究梯度提升树在月售电量预测中的具体应用。梯度提升树是基于分类与回归树的boosting模型，常用于分类与回归模型中。实验证明，梯度提升树在月售电量预测中具有优异的表现，不仅可以作为特征筛选的重要工具，也可直接用作预测模型的预测中。

1.引言

月售电量预测是指在对历史资料进行整理和分析的情况下，采用一定手段对未来月售电量进行估计或表述。无论是在国网公司的对标考核制度抑或在售电市场放开的今天，售电预测都是一项十分重要的工作，尤其是对于售电公司而言，售电预测准确率的高低将直接影响到偏差考核。偏差的电量值越大，罚款数额也就越高。准确地对月售电量进行预测对国网电力考核、以及售电公司的直接利益有着至关重要的现实意义与实用价值。

实际上早已有诸多学者对月售电量预测作了大量的研究与实际工作。主要通过神经网络模型寻找用电量与各影响因素之间的非线性关系进行拟合，即根据给定的训练样本，可调整神经网络的参数以使网络输出接近于已知的样本类标记。但是神经网络一般具有较多的参数，需要大量的样本进行训练，在成立不久售电公司中应用难度较高。ARIMA是典型的时间序列处理模型，它主要原理是许多非平稳序列在经过差分后会显示出平稳序列的性质，而对差分平稳序列可以使用AR、MA模型进行拟合。利用ARIMA根据历史的数据对未来数据进行预测并在其基础上进行改进。其优点是简单易行、样本需求量不高。但由于其本质是在前一序列基础上的上下浮动，因此对于波动较大的序列，预测精度将会受到影响。提出了一种基于改进灰色理论的中长期负荷预测方法研究，该方法在经典灰色预测GM（1，1）模型的基础上，首先利用三点平滑法对历史数据进行预处理，然后再构建基于等维新息矩阵的GM（1，1）模型，最后利用残差处理方法对预测结果进行修正。引入支持向量机模型，将历史负荷、预测日最高温度、平均温度、平均风速、平均相对湿度作为日最大(最小)负荷预测模型的输入建立最大(最小) 负荷的回归模型。

实际上分类与回归树（CART，Classify and Regress Tree）作为机器学习的常用算法之一，不仅在分类中有着出色的性能，在回归预测中也有优异的表现。尤其是基于CART的集成学习方法，在回归分析中大放异彩。本文主要提出梯度提升树(GBDT，Gradient Boosting Decision Tree)模型在月售电预测中的具体应用，首先对梯度提升树的基本原理作简单介绍；然后详细介绍影响因素的处理过程以及如何将算法应用到售电预测中；最后对某省会城市的历史月份售电数据进行实验。实验证明，梯度提升树在售电预测中具有优异的表现能力。

2.GBDT介绍

GBDT是在提升树（BDT, boosting decision tree）上的改进。提升树（BDT, boosting decision tree）主要利用加法模型和前向分步算法实现学习的过程，每次用之前所有树叠加的残差重新学习。由于提升树采取的损失函数是最小均方误差，所以每步拟合的就是上一次的残差（实际值-预测值）。但是针对一般的代价函数，往往没那么容易优化，因此Freidman提出了梯度提升算法：利用最速下降的近似方法，即利用损失函数的负梯度在当前模型的值，作为回归问题中提升树算法的残差的近似值，拟合一个回归树。

其主要的实现原理如下：

（1）初始化：

（2）对每颗树执行以下动作：

a）对每个样本，计算损失函数在当前模型的负梯度作为残差估计值；

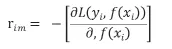
b）对于给定的rim拟合一颗回归树，得到树的叶子节点

c）对于叶节点，计算：

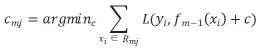
利用线性搜索估计叶节点值，使得代价函数最小化；

d）更新回归树

（3）输出梯度提升树：

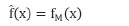
3.数据准备

3.1 数据采集

本实验收集了某省会城市从2008年12月到2017年6月份的用电数据，总计104个。然后分析影响用电的主要因素，重点采集了市商品房新开工面积、社会消费总额、大工业完成新装、增容、气温等影响因素。同时，考虑到节假日对大工业用电的影响，因此将每月的节假日天数作为独立属性加入影响因素中，累计共33个影响因素。

3.2 数据预处理

实际上基于决策树的集成模型对于数据的包容度非常高，不需要对数据做太多处理便可直接送入模型中进行训练。这里为了获取更好的性能主要对数据进行如下处理：

偏度检测：对于数值型因素，检测其是否为正太分布，如果不是的话，对数值进行相应的数据变换使其接近正太分布，如log1p、x^2等。时间因素：将年份、月份数据提取出来，作为单独的影响因素。类别数据：对于类别数据进行one-hot编码。

4.实验过程

该实验将本月用电量及影响因素作为属性，用于预测下一个月的用电量：

（1）将前83个数据作为训练数据，后20个数据作为预测数据。

（2）整个实验过程历经数据处理、模型调参、训练与预测等环节，并以均方误差根作为评判标准。

（3）为消除时序因素带来的影响，实验采用依次迭代的方法。每次训练完之后，只预测下一个月的用电量；如需继续预测，则需要对模型重新进行训练。

整个实验过程设置一个对照组，两个实验组：

对照组：直接利用传统的时间序列ARIMAX模型对下月售电量进行预测；

实验组1：用GBDT模型对下月售电量进行预测；

实验组2：将GBDT用于影响因素的筛选，并将筛选后的影响因素再送入ARIMAX模型中进行预测。

5.实验结果

基于传统的时序预测ARIMAX模型与基于GBDT模型预测的比较，对照组与实验组1结果如下：

基于GBDT模型的RMSE：49320.2

基于ARIMAX模型的RMSE：57121.2

图1 对照组与实验组1预测曲线Fig.1 Predictive curve of control group and experimental Group 1

总体而言GBDT模型比ARIMA性能要好，损失代价更少。同时，ARIMA前期拟合度较高，但是后期效果GBDT更佳。这是因为对于ARIMA模型，其训练数据数量要求并没有很高，即很小的数据也能有较好的拟合效果。但是随着训练数据的增加，GBDT的回归预测能力越来越强，与实际曲线也越来越接近。实验证明GBDT在月售电预测上有着优异的性能。

传统的时序预测ARIMA模型在有无GBDT模型进行影响因素筛选情况下，对照组与实验组2结果如下：

基于GBDT+ARIMAX模型的RMSE：47657.5

基于ARIMAX模型的RMSE：57121.2

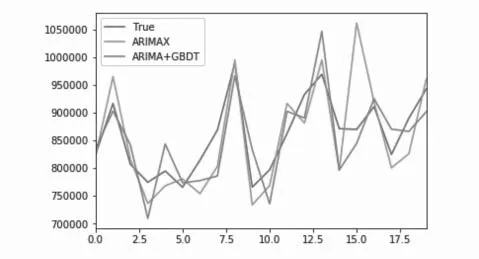
图2 对照组与实验组2预测曲线Fig.2 Predictive curve of control group and experimental Group 2

可以看到，基于GBDT的ARIMAX模型在与真实值拟合上的趋势也比单纯的ARIMAX预测效果更好。对于GBDT模型，由于每次分裂都是其属性选择的过程，因此模型本身具有很强的特征工程的能力。通过将模型选择后的特征重新送入新的训练器，也会有较好的结果。

6.总结

GBDT作为决策树模型的集成学习器，在回归方面表现了非常优异的性能。本论文提出逐步预测的方式、以消除时间因素带来的影响，在月售电预测上展现了比ARIMAX更加优异的性能。该模型不仅可以用作对售电量的精准预测，还可以作为特征选择算法对众多影响因素进行特征筛选，可根据实际场景需求进行完善。