几种改进的朴素贝叶斯分类器模型
2018-11-22四川九洲电器集团有限责任公司高晓利赵火军
四川九洲电器集团有限责任公司 高晓利 王 维 赵火军
介绍了朴素贝叶斯分类器模型,分析归纳了几种基于较宽松属性间关系的改进算法,包含TANF算法、HCS及SP算法;同时在研究Adaboost集成技术的基础上,详细介绍了基于集成技术的改进朴素贝叶斯模型,该技术能够提高朴素贝叶斯分类器的分类 性能。
0 引言
在数据挖掘领域,分类是一个重要的研究方向,其关键问题是:构造一个分类器,也就是一种分类算法或者说构建一个分类模型,然后给属性集描述的实例指定最合适的标签。
在众多分类方法的建模过程中,朴素贝叶斯分类器(Naïve Bayesian Classifier)由于资源利用率高,计算精确度高,具有坚实的数学理论基础,从而得到了广泛的应用。朴素贝叶斯分类器是基于一个假定:在给定特征值条件下,属性值之间相互条件独立,但在工程应用中,属性值之间相互关联,要想在工程中应用,必须改进朴素贝叶斯分类器,使之在假定条件不满足的情况下,依然具有较高的工程应用价值,就成为贝叶斯分类器的一个重要研究方向。
文章分析归纳了现在流行的几种改进朴素贝叶斯分类器模型,大体上可以分为以下两类:一是研究属性值的非条件独立,即具有较宽松条件限制的分类器;二是研究提高整体性能的集成方法,即使用分类器集成技术,将不同的分类器有机组合成一个新的分类器,从而改善整体性能。本文的结构安排如下:首先介绍朴素贝叶斯分类模型,其次分析归纳几种基于属性间关系的改进算法,然后介绍一种非常流行的Adaboost集成技术,通过该技术提高朴素贝叶斯分类器的工程应用价值,并且为这种分类器以后发展提出自己的看法。
1 朴素贝叶斯分类模型
朴素贝叶斯分类器原理是一种统计学方法。贝叶斯定理是分类器建模的理论基础,它利用条件概率原理,利用先验信息和样本数据信息确定事件的发生的概率。另外,朴素贝叶斯模型是一种生成模型,采用直接对联合概率建模,以获得目标概率的方法。

其中α是正则化因子。依据概率的链准则,式((1)可以表示为:
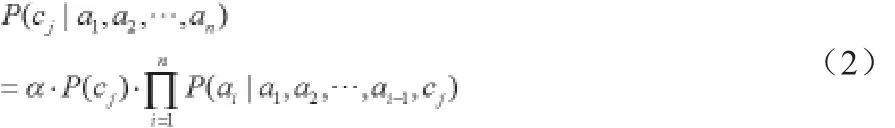
现假定只有两类,标记为0和1;α1到αk表示测试集属性;记则有:

其中z为常数,将(3)式和(4)式两边取对数后相减得:


(6)式两边取指数,则有:

假定属性Aj具有种可能的属性值,那么当:

这里I是一个指标函数,且满足sigmoid函数,即:
(1)如果φ为真,那么I(φ) = 1;
(2)如果φ为假,那么I(φ) = 0。
实际上,(8)式描述的是一个具有sigmoid型的感知器激活函数,因此,朴素贝叶斯分类器在特定输入场合上的表现能力等价于感知器。
2 基于属性间关系的改进算法
朴素贝叶斯网络要求的条件独立的假设在现实世界很难满足,在工程上,为了提高贝叶斯分类器的性能,降低条件之间的联系。国内外机器学习的工作者先后提出了不同的方法,其中树扩展的朴素贝叶斯(Tree Augmented Naïve Bayes,简称TAN)是一类高效的、主流的方法。其基本思想是:以图论为基础,把不包括类的属性组织为树,每个节点不但拥有类属性作为父节点,而且最多拥有一个其他属性作为父节点,而类作为根节点,没有父节点。目前实现TAN的常用方法有:由Friedman和Goldszmidt提出的TANF算法;由Keogh和Pazzani提出的HCS及SP算法,分别给予简单介绍。
2.1 TANF
Friedman和Goldszmidt结合贝叶斯网络的相关性和朴素贝叶斯分类器的特点,并且两者进行有机整合,提出了TANF方法。该方法是在1968年提出的Chow-Liu方法为基础上,将该方法将两个属性的条件信息用条件互信息代替。

TANF算法基本思路是:一、计算两个属性节点的条件互信息,在上训练模型;二、在类节点与每一属性节点之间加一条边。
具体构造TANF过程如下:
Step3:根据图论中的Dijkstra算法,构造最大权值生成树;
Step4:选择合适的根变量,并假定所有的方向是以根变量为向外发出的方向;
Step5:完善以C为标识的顶点和从C到Xi的弧,从而得到TANF模型。
2.2 HCS
Keogh和Pazzani在2001年提出了爬山搜索算法(HCS)实现TAN分类器构造。每个节点最多有一个非类节点为父节点,因此最多增加N-1条(N是节点个数)相关联的弧,最少增加0条弧(即朴素贝叶斯分类器)。HCS算法基本步骤:
Step1:初始化。将网络初始化为一个朴素贝叶斯网络;
Step2:评估当前的分类器;
Step3:完善当前分类器中合法的弧;
Step4:如果存在一条弧,使得分类器性能提高,则将该弧加入当前分类器中,转至step2,否则返回。
以朴素贝叶斯分类器初始化网络,孤立点集O初始化为所有属性点集X1,…, Xn,利用交叉验证评价从Xi到Xj的每条弧,如果不存在能够提高分类器性能的弧,则表明当前分类器是最优的;否则,表明存在能够提高分类器性能的弧,保留这条弧,并提出这条弧所指向的那个节点。当O中包含当且仅当只有一个节点时,循环终止。
2.3 SP
SP算法是Keogh和Pazzani提出的另一种树扩展朴素贝叶斯分类器。同爬山搜索算法类似,SP也是通过剔除孤立点集中的顶点,寻找最优弧来提高分类器的精度。把这个过程分为两个步:第一步,寻找一个最优的超父节点;第二步,寻找最优子节点,找到这个子节点要与超父节点相对应。
在给定扩展贝叶斯网络模型中,如果从节点Xsp到每个孤点扩展了孤,则该节点Xsp称为超父节点。
如果依次从该节点Xsp扩展弧到每个子节点,并且计算该子节点在预测精确上的影响,由最佳弧指向的节点被称为该超父节点Xsp的最优子节点。
SP算法基本步骤:
Step1:以朴素贝叶斯模型初始化网络;
Step2:评估当前的分类器;
Step3:超父节点Xsp是各个节点中能够提升准确度最大的那个节点;
Step4:计算从Xsp到每个孤立点的弧,如果提高了准确度,则保留它,继续step3;否则,返回当前分类器。
首先以朴素贝叶斯模型初始化网络,孤立点列表O完全初始化为节点X1,…, Xn。其次,找出超父节点Xsp。接着寻找Xsp的最优子节点。如果增加从Xsp到最优子节点的弧后,提高了分类器的精度,则剔除最优子节点,只是把此弧加入当前分类器中,再次进入SP循环。如果分类准确度没有提高或者,则返回当前分类器。
3 使用集成技术的分类器
分类器集成学习,也就是把不同的分类器进行组合,形成的最终的分类器。所谓集成也就是将多个不同的弱学习算法,通过一定的方法和手段,利用相关的技术,最终形成一个组合的强学习算法。现在流行的集成方法很多,其中Boosting和Bagging是主流的集成技术,下面我们主要讨论Boosting技术中的Adaboost算法是如何提高模型的分类精确度的。Adaboost算法的核心内容是:
输入:有N个训练例:

N个例子上的分布D:ωi为每个训练实例的权重,T为次数,N为总的次数。
初始化:ωi初始化为
Do for t =1,2,…, T do
(1)给定权值ωi(t)得到一个假设:

(2)求H(t)的误差为:
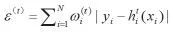
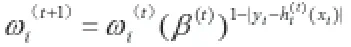
(4)正规化ωi(t+1)使其综合为1.0
End Do
输出:

在这里,假设每一个分类器都是实际有用的,ε(t)<0.5,即在每次分类的结果中,正确分类的结果始终大于错误分类的结果,那么可以得到β(t)<1,当增加时,ωi(t+1)增加,因此显然算法满足增强的思想。
(1)利用Adaboost增强朴素贝叶斯时,h(t)采用公式(10)计算得出;
(2)算法的输出是指:当给定一个新的x,通过算法的第5步,就可以利用以前的每次增强学习效果,通过投票输出最终的假设结果;
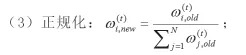
(4)算法最终的联合假设H可以给定为:

那么:

4 结束语
本文详细分析了几种改进或增强朴素贝叶斯分类算法,这几种方法是从属性间关系或分类器整体技术出发。目前,又有许多基于这两方面的改进策略。如Wang和Webb等提出了一种准懒惰式的限制性贝叶斯网络分类器的条件概率调整方法,在某些情况下可以减小误差分类器。另外,在分类器整体技术方面,Fan H, Ramamobamaro将显示模式技术应用到分类器的构造中,在数据集合中部分属性值表现的比较活跃,这些属性值组合成的序列被称为显现模型。
