立式轴流泵装置进出水流道多方案优选
2018-11-22孙丹丹汤方平
孙丹丹 ,高 慧 ,王 刚,杨 帆 ,汤方平
(1.徐州市水利建筑设计研究院,江苏 徐州 221000;2.扬州大学,江苏 扬州 225127)
低扬程泵站具有扬程低、流量大的优点,在防洪排涝、水环境治理等工程领域应用较多,其中适用于低扬程泵站的泵装置型式中立式轴流泵装置的应用最为广泛。立式轴流泵装置水力性能对保证泵站的安全、稳定和高效运行具有重要意义[1],低扬程立式轴流泵装置中最常用的流道型式为肘形进水流道和虹吸式出水流道,目前,对该类型立式轴流泵装置的研究多集中于其进出水流道内部流动特性分析、叶轮选型、进水流场的影响等方面,张弛等[2]对大型泵站肘形进水流道设计进行了研究;杨帆、王丽慧等[3-5]对轴流泵装置进行了全流道数值计算,并进行了物理模型试验与数值预测结果的差异性对比;冯俊、刘军等[6-7]学者分别对轴流泵装置后置导叶及模型试验进行了研究。借鉴很多学者的研究成果,本文以刘山北站为背景,开展流道的数值优化研究,刘山北站工程泵站的设计扬程为4.6 m,选用5台1800ZLQ机械全调节立式轴流泵机组,单机设计流量为9.66 m3/s,配套TL1000-28型高压电机5台套,单机功率1000 kW,电机转速214.3 r/min,泵站采用肘形流道进水,虹吸式出水流道。本文依据该站基本参数,建立数值模型对进出水流道进行水力优化,对提高该泵站的水力性能和降低泵站的能耗具有重要的意义。
1 泵装置的基本参数
在ANSYS DM中完成进水流道三维模型的构建,叶轮和导叶的三维模型均在ANSYSTurbogrid中建立,水力模型为ZM6.6-Y981水力模型,叶轮名义直径为1800 mm,叶顶间隙设置为0.2 mm,叶片数Zy=4,叶片安放角β=0°,额定转速n=214.3 r/min;导叶体叶片数Zd=7。考虑虹吸出水流道上升端的仰角限制取转弯段角度为46°。立式轴流泵装置由肘形进水流道、叶轮、导叶体、虹吸式出水流道组成。
2 数值模拟计算与网格剖分
2.1 控制方程与湍流模型
泵叶轮内部流动是三维非定常湍流流动,但是在水泵稳定运行(转速恒定)后可认为叶轮相对运行是定常流动,采用“Stage”交界面处理叶轮与进水流道、导叶体之间动静耦合流动的参数传递。控制方程的离散采用基于有限元的有限体积法。扩散项和压力梯度采用有限元函数表示,对流项采用高分辨率格式(High Resolution Scheme)。流场的求解使用全隐式多重网格耦合方法,将动量方程和连续性方程耦合求解,克服了传统SIMPLE系列算法需要“假设压力项—求解—修正压力项”的反复迭代过程,同时引入代数多重网格技术,提高了求解的稳定性和计算速度。
泵装置内部流动介质为水,可简化为不可压缩的牛顿液体,采用的控制方程为雷诺时均N-S方程,湍流模型采用标准k-ε湍流模型。
2.2 计算方法与边界条件
为了更好地模拟立式轴流泵装置内部流动,将计算流场的进口设置在进水流道延伸段的进口断面,采用总压进口条件,总压设置为1.0 atm;将出口设置在出水流道延伸段的出口断面,出口断面采用质量流量出流。湍流模型不适用于壁面边界层内的流动,所以对壁面需进行处理才能保证模拟的精度。泵装置的进出水流道、叶轮外壳及导叶体均设置为静止壁面,应用无滑移条件,近壁区采用可伸缩壁面函数。
2.3 模型建立与网格剖分
采用ANSYS DM与ANSYS ICEM软件对肘形进水流道、虹吸式出水流道和弯头进行实体建模与网格剖分。采用ANSYS TurboGrid软件对叶轮和导叶体进行建模与网格剖分。经网格数量无关性验证后确定计算区域的网格节点数与体网格单元数,如表1所示。
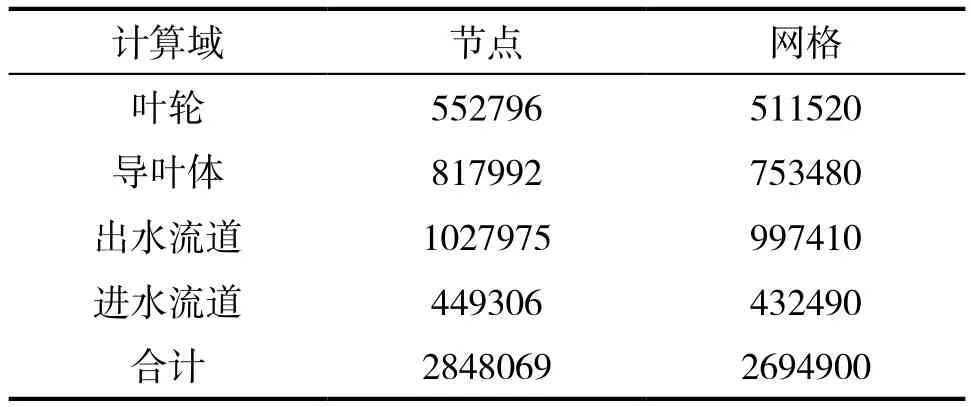
表1 网格结点与网格数
最后确定了立式轴流泵泵装置的网格单元总数为2848069,体网格单元数为2694900。满足网格数量无关性检验要求。
3 肘形进水流道优化设计
3.1 优化方案的选择
对原始设计方案进行必要的流道安装尺寸和流道断面面积检查后规划设计方案一,叶轮中心距地板的高程与叶轮直径的比值为1.583,进水流道总长度与叶轮直径的比值为4.6;在方案一的基础上将进水流道最低端下降20 cm,同时保证断面面积均匀的变化,形成方案二,此时叶轮中心距地板的高程与叶轮直径的比值为1.694;在方案二的基础上将进水流道最低端继续下降20 cm,同时保证断面面积均匀的变化,形成方案三,叶轮中心距地板的高程与叶轮直径的比值为1.805。各方案进水流道的对比如图1、图2所示。
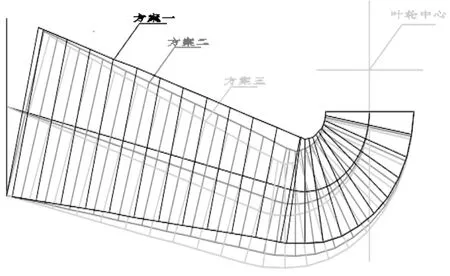
图1 肘形进水流道不同方案侧视对比图
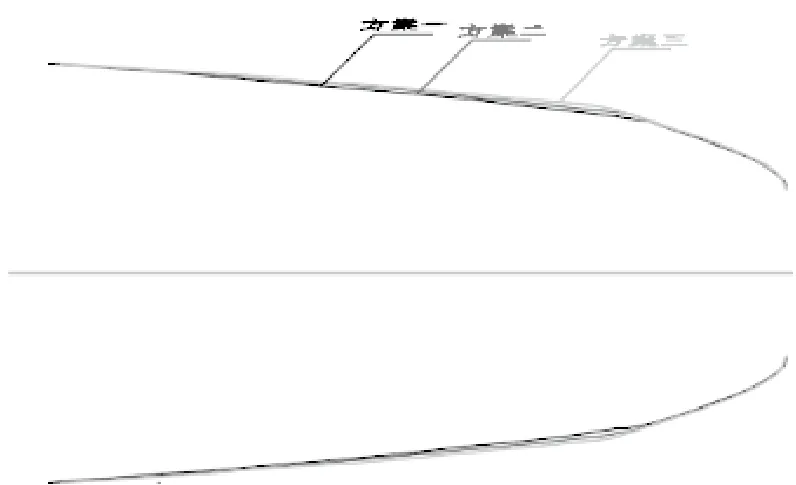
图2 肘形进水流道不同方案俯视对比
3.2 优化结果分析
模拟计算结果表明肘形进水流道流态较好,方案一在靠近出口的弯肘内侧存在低压区,但其压力值相对较高,不会在叶轮进口产生汽蚀,同时进口的流速均匀度高达96%左右,流速均匀度较高,说明叶轮进口进水流态较好。各方案肘形进水流道流线图和静压分布云图如图3所示,可知,方案三的叶轮进口处流速分布相比较方案一和方案二最好,方案二与方案三低压区面积大小类似且明显比方案一要小,方案二最小压力相比较方案一要大许多,流速均匀度也有所提高,水力损失相比较方案一也小了一些,但是效果不明显。方案三较方案二最小压力并没有明显的改善,流速均匀度相比较方案一较好,相比较方案二没有明显变化,水力损失相比较方案二也小了一些,但是效果不明显。

图3 各方案肘形进水流道流线图和静压分布云图(Q=Qd)
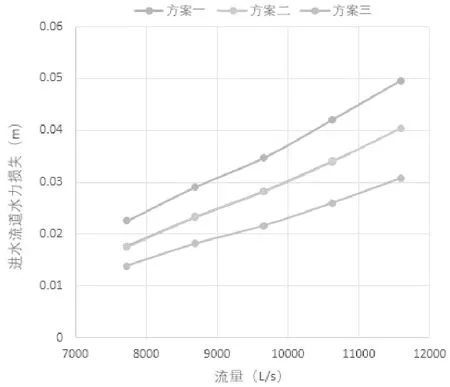
图4 不同方案的肘形水力损失对比曲线
3个方案肘形进水流道的水力损失和叶轮进口流速均匀度如图4、图5所示。肘形进水流道水力损失与流量成单调递增关系,计算工况下水力损失为0.02~0.05 m。方案一水力损失最大,方案二和方案三均优于方案一,方案三水力损失最小,3种方案整体上相差不大,对整体泵装置的性能影响较小。肘形进水流道出口流速均匀度与流量成单调递增关系,计算工况下流速均匀度为95.4%~96.7%。各计算工况下方案一进水流道出口流速均匀度最差,方案二和方案三明显都优于方案一,方案二进水流道出口流速均匀度最好。

图5 不同方案的叶轮进口流速均匀度对比曲线
4 虹吸式出水流道的优化设计
4.1 优化方案的选择
出水流道模型建立时考虑真空破坏阀的位置,并兼顾出水流道内水流平顺过渡。将原始方案定为方案一,驼峰顶部断面的流速为2.35 m/s;在保持其他参数不变的情况下,改变驼峰顶部断面的流速为2.0 m/s,驼峰顶部断面的高度不变,宽度变宽,驼峰处的转弯半径相应的稍微增大,定为优化方案二;相对于优化方案二,将驼峰顶部断面的流速由2.0 m/s变为2.2 m/s,并将驼峰断面的高度由0.76倍叶轮直径变为0.67倍叶轮直径,驼峰顶部位置不变,驼峰底部的形线基本保持不变,驼峰顶部的形线转弯半径变小,定为优化方案三;且相对于优化方案二,保持驼峰位置不变,将出水口向右平移2 m,驼峰前的部件均不改变,驼峰后的下降倾角变小,出水流道变得更长,定为优化方案四;相对于优化方案四,将驼峰顶部位置向右水平移动1 m,出水流道出水口相应的也向右移动1 m,此时出水流道形式变化较大,出水流道的上升倾角变小,出水流道变得更长,定为优化方案五;相对于优化方案三,将出口流速提高至0.8 m/s,保持出口断面的顶部位置和出口宽度不变,出口底部相应的抬升,出水口断面面积减小,定为优化方案六。各方案出水流道对比如图6、图7所示。
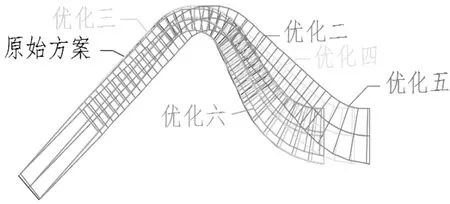
图6 虹吸出水流道不同方案侧视对比图
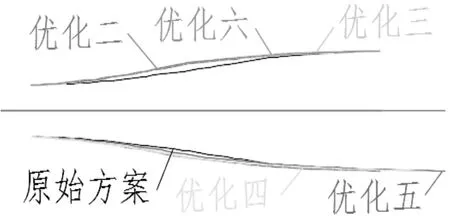
图7 虹吸出水流道不同方案俯视对比图
4.2 优化结果分析
各优化方案流道内部流线如图8所示,原始方案出水流道流线紊乱,驼峰下降段有回流;优化方案二在流态上有所改善,回流没有被消除;优化方案三流线相对于方案二紊乱,驼峰下降段回流未消除;优化方案四流线相对于方案二变得稍许均匀,但是驼峰下降段的回流仍未被消除;优化方案五流线相对于方案四变得更不均匀,驼峰下降段回流仍存在;优化方案六流线相对于方案三变得更加均匀,且驼峰下降段的回流被消除。
图9为各优化方案流道壁面静压云图,可见,原始方案和优化方案二流道壁面静压分布都不均匀,优化方案三和优化方案四流道壁面静压分布稍微均匀一些,优化方案五流道壁面静压分布梯度更大,而优化方案六流道壁面静压分布梯度则变小。
图10为各优化方案中间断面的静压云图,可见,原始方案流道中间截面的静压分布递变不均匀,优化方案二流道中间截面的静压分布也较差,优化方案三流道中间截面的静压分布递变相对较为均匀,但整体效果不明显,优化方案四则相对较为均匀,整体效果更加明显,而优化方案五流道中间截面的静压分布递变不明显,优化方案六流道中间截面的静压分布递变均匀。
不同方案虹吸出水流道设计工况下的水力损失对比如图11所示。通过对比可以发现虹吸出水流道优化方案四水力损失最小,但是其驼峰下降段有回流,优化方案六驼峰下降段的回流被消除,同时水力损失相对于优化方案四仅增加了0.02 m,故而应用优化方案六较为合理。
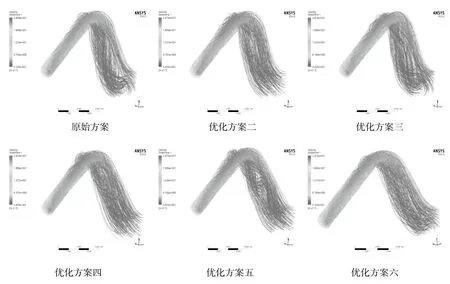
图8 不同方案Qd流道内部流线图
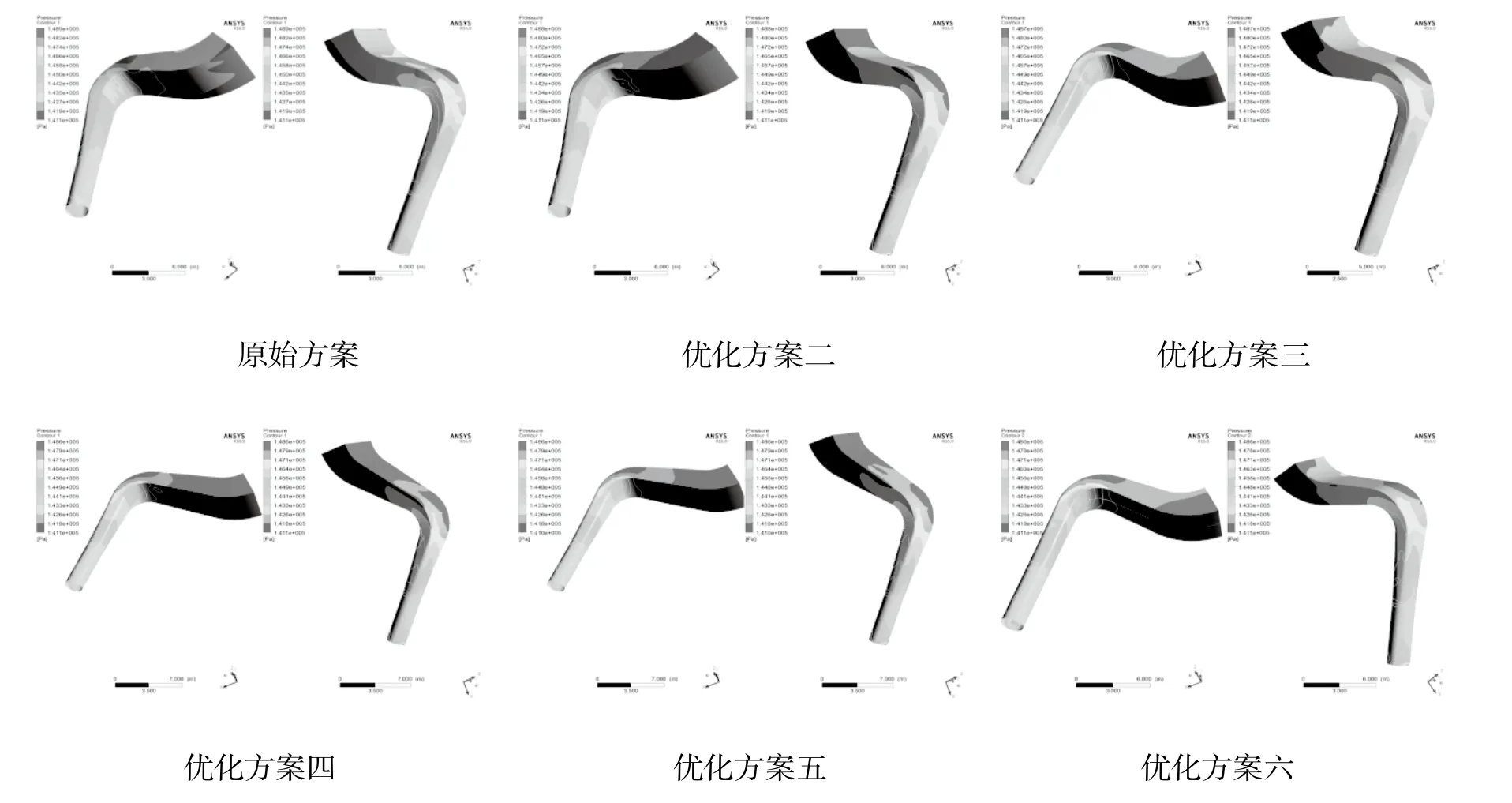
图9 不同方案Qd流道壁面静压云图(Qd)


图10 不同方案中间断面的静压云图(Qd)
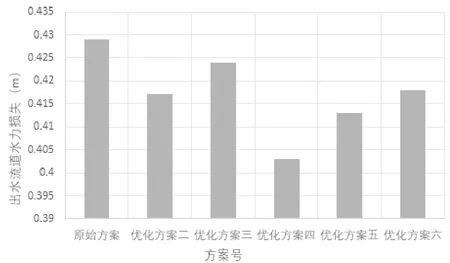
图11 虹吸出水流道不同方案水力损失对比
5 结论
(1)肘形进水流道方案二和方案三均优于方案一,但方案二流速均匀度提高最为明显,故肘形进水流道优选方案二,即流道加长100 cm,流道最低点高程下降20 cm。
(2)基于对虹吸式出水流道的优化比较分析,虹吸式出水流道优化方案六消除了虹吸下降段的回流现象,同时水力损失相对于水利损失最小的优化方案四仅增加了0.02 m,故优选方案六,即出水流道长度不变,驼峰位置不变,高度降低;出口流速加大,出口高度减小,即流道出口底部高程抬高45 cm。
